|
|
||||
|
||||
|
|
On désire construire une piscine couverte de longueur L=25 m, de largeur l=10 m et de profondeur utile ( hauteur d'eau) H=4,5 m. Le bâtiment qui l'abrite doit permettre d'avoir 5 m de plage sur tous les côtés de la piscine. 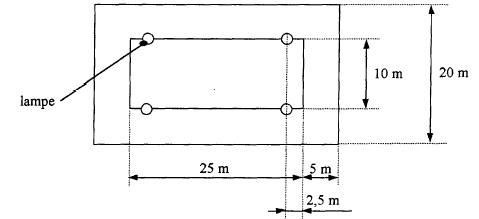 reau = 1000 kg m-3 ; g= 10 m/s² ; pression atmosphérique p0=105 Pa.
corrigé pression exercée par l'eau au fond de la piscine : p=reau gH= 1000*10*4,5 =4,5 104Pa surface du fond : S= 25*10 = 250 m² force pressante exercée par l'eau sur le fond : F= p S= 4,5 104 *250=1,12 107 N. résultante des forces pressantes F1 exercées sur chaque petite paroi verticale : pression à mi-hauteur d'eau : H1=4,5/2 = 2,25 m p1=reau gH1= 1000*10*2,25 =2,25 104Pa surface de la petite paroi verticale : S1 = 10*4,5 = 45 m² F1 = p1 S1 =2,25 104 *45 = 106 N. résultante des forces pressantes F2 exercées sur chaque grande paroi verticale : pression à mi-hauteur d'eau : H2=4,5/2 = 2,25 m p2=reau gH2= 1000*10*2,25 =2,25 104Pa surface de la grande paroi verticale : S2 = 25*4,5 = 112,5 m² F2 = p2 S2 =2,25 104 *112,5 = 2,53 106 N. la résultante des
forces F1 ( de même pour F2 ) s'appliquent en un
point situé à égale distance des bords et au tiers de la hauteur à
partir du fond.
section bonde =3,14*0,06²= 1,13 10-2 m² ; débit : 0,05 m3/s vitesse : 0,05 / 1,13 10-2 = 4,42 m/s. pression au niveau de la bonde appliquer le théorème de Bernoulli entre la bonde ( notée B) et la surface libre (notée A) La vitesse est quasiment nulle en A car la surface libre est très supérieure à la section de la bonde; pA=105 Pa ( pression atmosphérique ½rvA²+pA+rgzA=½rvB²+pB+rgzB pB= pA+rg(zA-zB ) +½r(vA²-vB²) pB= 105 + 1000*10*4,5 +0,5*1000*(-4,42²) pB= 105 + 4,5 104-9768=1,35 105 Pa. volume de la piscine : 25*10*4,5 =1125 m3. durée de la vidange : 8*3600 = 28800 s débit volumique : 1125/28800=0,039 m3/s=39 L/s. le débit de la pompe (50 L/s) est convenable.
|
|||
|
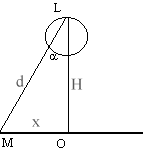
On place à la verticale de chacun des grands bords du bassin et à 2,5 m des angles, quatre lampes permettant d'éclairer le bâtiment. Elles sont situées à une hauteur H=8 m au dessus du sol. L'intensité lumineuse due à chaque lampe est, suivant la verticale I0 = 7000 cd. Dans une direction faisant un angle a avec la verticale, l'intensité lumineuse due à chaque lampe est donnée par la relation I=I0 cosa.
corrigé E éclairement d'une surface exprimé en lux (lx) ou flux énergétique reçu par unité de surface éclairement E0 à la verticale de la lampe = I0 / H² = 7000/8² = 109,4 lx. éclairement EA : Connaissant l'intensité lumineuse I (cd) et distance d (m) d’un luminaire à la surface éclairée, on peut calculer l'éclairement en divisant l'intensité lumineuse I par le carré de la distance d (en mètres). d'une part l'intensité lumineuse diminue I = I0 cosa d'autre part la distance devient d= H/cos a E = I/d² = I0 cos3a / H² =E0 cos3a avec tan a = x/H = 11,2 /8=1,4 et cos a = 0,581 E= 109,4*0,5813=21,5 lx.
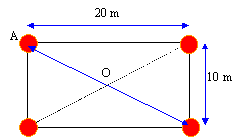
OA = 0,5 racine carrée (20²+10²)= 0,5 *racine carrée 500 = 11,2 m. éclairement au centre de la piscine du aux 4 lampes : 4*21,5 = 86 lx. flux F =pI0 =3,14*7000 = 21980 lm efficacité lumineuse k= 27,5 lm W-1 puissance d'une lampe :P= 21980 / 27,5 = 800 W.
|
||||
|
Une solution de détartrant concentré utilisé pour l'entretien de la piscine a un pH=1,8. En utilisation normale ce produit doit être dilué.
corrigé pH= - log [H3O+], la concentration en ion oxonium s'exprime en mol/L. pH =1,8 donc le détartrant est acide. acide entierement dissocié donc c= 10-pH= 10-1,8 = 1,58 10-2 mol/L. le facteur de dilution est 24/1 = 24 la solution diluée est 24 fois moins concentrée que le détartrant : C1 = 1,58 10-2 / 24 =6,58 10-4 mol/L. pH= -log C1 = -log 6,58 10-4 = 3,18. équation du dosage : HO-+H3O+ --> 2H2O à l'équivalence les quantités de matière des réactifs sont en proportions stoechiomètriques C1V1 =C2V2 soit C1=C2V2 /V1=10-3*12,9/20=6,45 10-4 mol/L. accord avec le résultat précédent.
|
||||
| |
||||
|
chimie des solutions aqueuses : produit ionique de l'eau à 25 °C : Ke = 10-14. masses molaires en g/mol :H=1 ; O=16 ; Na=23 ; Cl=35,5 ; S=32,1. Les effluents liquides d'un laboratoire atteignent une épaisseur de 0,8 m dans un bassin de récupération de longueur 1,6 m et de largeur 1,1 m. Une mesure du pH de la solution réalisée à l'aide d'un papier indicateur de pH donne la valeur 2.
corrigé l'ion oxonium H3O+ est responsable de l'acidité. [H3O+]=10-pH= 10-2 mol/L l'ion hydroxyde HO- est minoritaire en milieu acide :[HO-]=10-14/10-2=10-12 mol/L la solution d'acide chlorhydrique est électriquement neutre donc [Cl-]=[H3O+]=10-2 mol/L ( ion chlorure) équation de la réaction de dosage : H3O+ +HO- = 2H2O Qté de matière d'acide (mol) = volume (L) * concentration (mol/L) volume = 1,6*1,1*0,8 =1,408 m3 = 1408 L 1408*0,02 = 14,08 mol d'acide donc 14,08 mol ion hydroxyde. A l'équivalence les quantités de matière d'acide et de base sont en proportions stoechiométriques CaVa= CbVb d'où Ca =0,01*12,6/10 =0,0126 mol/L pHthéorique = -log0,0126 = 1,9. Qte de matière d'acide dans le bassin : 0,0126*1408 =17,74 mol Qté de matière hydroxyde de sodium : 17,74 mol masse molaire hydroxyde de sodium NaOH : 23+1+16 = 40 g/mol masse de soude nécessaire : 40*17,74 = 709 g. |
||||
|
Chaleur
corrigé Ec=½mv² masse : [M] ; vitesse au carré : [L]² [T]-2 ; énergie [M] [L]² [T]-2 puissance = énergie (J) / durée (s) soit : [M] [L]² [T]-3 débit volumique : volume(m3) / durée (s) soit [L]3[T]-1. volume local V=11*7*3=231 m3. quantité de chaleur Qa = cair V rair (20-0)=1000*231*1,25*20=5,77 106 J. volume paroi béton : Vb=(11+11+7+7)*3*0,2=21,6 m3. quantité de chaleur Qb = cbéton Vb rbéton (10-0)=800*21,6*2300*10=3,97 108 J. 100 fois plus grande que la valeur précédente. Qa négligeable devant Qb. conduction, convexion et rayonnement résiqstance surfacique : R= e/l+1/hi+1/he= 0,2 / 1,1 + 0,11+0,06=0,352 W-1m²K. coefficient de transfert K= 1/R = 1/0,352 = 2,84 W m-2 K-1. flux thermique surfacique : F= K(qchaud-qfroid)=2,84 *(20-0)=56,84 Wm-2. surface totale des parois : (11+11+7+7)*3=108 m² puissance thermique : 56,84*108= 6138 W. puissance thermique transférée par un radiateur : débit massique * capacité thermique de l'eau * différence température 0,02*4180*(70-40)=2508 W. il faut donc prévoir trois radiateurs pour compenser les pertes thermiques.
|
||||
|
Dans une installation de chauffage central l'eau sort de la chaudière avec un débit volumique qv=18 L/min, à une pression p=5 105 Pa, dans un tuyau de diamètre intérieur D= 20 mm. Les radiateurs sont branchés en dérivation. Le diamètre intérieur du tuyau qui les parcourt est d =5 mm. On considère l'eau comme un fluide parfait de masse volumique reau=1000 kgm-3. g= 10 m/s².
corrigé section du tuyau de sortie de la chaudière : S= 3,14 10-4 m². débit volumique (m3/s)= section (m²) fois vitesse (m/s) débit : 18 10-3 / 60 = 310-4 m3/s. v= 310-4 / 3,14 10-4 =0,955 m/s. le débit volumique reste constant. un seul radiateur ouvert : section 3,14 *(2,5 10-3)²= 1,96 10-5 m². vitesse : 310-4 /1,96 10-5 = 15,3 m/s. deux radiateurs ouverts : section 2* 1,96 10-5 = 3,92 10-5 m². vitesse : 310-4 /3,92 10-5 = 7,65 m/s. pression : appliquer le théorème de Bernoulli entre la sortie de la chaudière ( notée A) et le radiateur (noté B) ½rvA²+pA+rgzA=½rvB²+pB+rgzB pB= pA+rg(zA-zB ) +½r(vA²-vB²) un seul radiateur : pB= 5 105 + 104(-3)+500 ( 0,955²- 15,3²)=3,53 105 Pa. deux radiateurs : pB= 5 105 + 104(-3)+500 ( 0,955²- 7,65²)=4,41 105 Pa.
|
||||
|
|