|
|
||||
|
||||
|
|
Etude d'une solution de permanganate de potassium : le dosage de cette solution peut se faire par une réaction d'oxydoréduction en utlisant une solution contenant des ions ferreux Fe2+ en milieu acide. MnO4- / Mn2+ : E01=1,51 V ; Fe3+ / Fe2+ : E02=0,77 V
Etude d'un équilibre de précipitation : les calculs rénaux sont essentiellement constitués d'oxalate de calcium CaC2O4, composé peu soluble constitué d'ion Ca2+ et C2O42-. On néglige le comportement basique des ions oxalates C2O42-.
produit de solubilité de CaC2O4 : Ks= 3,6 10-9. corrigé MnO4- est l'oxydant le plus fort ; Fe2+ est le réducteur le plus fort. MnO4- + 8H+ + 5e- = Mn2+ + 4H2O 5Fe2+ = 5 Fe3+ +5 e-. MnO4- + 8H+ + 5Fe2+ = Mn2+ + 5 Fe3+ + 4H2O E = 1,51 -0,77 = 0,74 V DG0 = -nFE = -5*96500*0,74 = -357000 J. DG0 = -RT ln K ln K= DG0 /( -RT ) = -357000 /(-8,31*298)=144,18. K= 4 1062. CaC2O4(s)=Ca2++C2O42-. Ks=[Ca2+][C2O42-]=s² = 3,6 10-9 d'où s= 6 10-5 mol/L. Dans une solution contenant des ions calcium tels que [Ca2+] >> s : le produit [Ca2+][C2O42-] est constant pour une température donnée ; si [Ca2+] >>s alors s'=[C2O42-] << s. si [Ca2+] = 0,02 mol/L alors s' = 3,6 10-9 /0,02= 1,8 10-7 mol/L.
|
|||
|
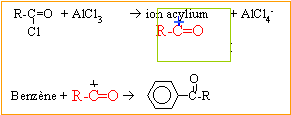
Le styrène C6H5-CH=CH2 peut être obtenu à la suite des opérations suivantes :
corrigé A est l'acide éthanoïque CH3-COOH B est le chlorure d'éthanoyle CH3-COCl C est une cétone : test positif avec la 2,4-DNPH mettant en évidence le groupe carbonyle; test négatif avec la liqueur de Fehling ( le test est positif avec un aldehyde) C6H5-CO-CH3.
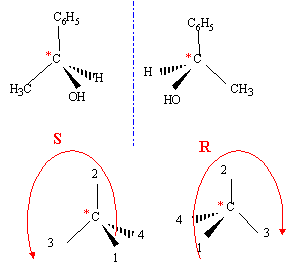
D est : C6H5-CHOH-CH3.
numéroter de façon décroissante chacun des quatre substituants selon son numéro atomique. OH (1) ; C6H5- (2) ; CH3 (3) ; H (4). On place alors l'atome (ou le groupement) de numéro le plus élevé derrière. On regarde dans quel sens, sens horaire ou trigonométrique, on passe du numéro 1, au 2, au 3. - Si le sens de rotation est le sens horaire (ou anti-trigonométrique), le carbone est Rectus (R), - Si le sens de rotation est le sens trigonométrique (ou anti-horaire), le carbone est Sinister (S). C6H5-CHOH-CH3 --> C6H5-CH=CH2 + H2.
|
||||
|
Les grandeurs algébriques sont écrites en gras et en bleu. Un microscope optique est constitué d'un objectif de distance focale f'1= O1F'1=1 cm et d'un oculaire de distance focale f'2= O2F'2 = 4 cm. La distance entre les centres optique est O1O2 =21,7 cm.
h= 6,62 10-34 Js ; masse de l'électron m= 9 10-31 kg. corrigé 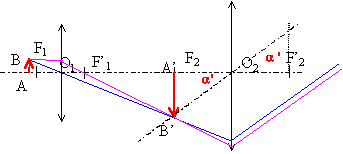
L'image intermédiaire est réelle et située au foyer objet de l'oculaire ; l'image définitive est virtuelle, rejetée à l'infini. puissance du microscope: Soit a' l'angle en radians sous lequel est vue l'image A'B' donnée par l'objectif L1. tan a' = A'B' / F2O2 = A'B'/f'2. L' angle a' étant petit tan a' voisin de a' radians. Par définition, la puissance du microscope est égale au rapport du diamètre apparent de l’image instrumentale a' (dans le cas d’un angle petit) à la taille de l’objet observé P= a' /AB puissance en dioptrie (d) et AB en mètre P= A'B'/ AB* 1/f'2 = g /f'2 ; g est le grandissement de l'objectif g = O1A'/O1A =( O1F'1+F'1A' )/O1A =(f'1+D) / O1A voisin de D / f'1. P =D / (f'1f'2 ) Soit l'angle a sous-tendu par l'objet étudié lorsqu'il est placé à la distance minimale de vision nette d ; soit l'angle a' sous lequel l'image de ce même objet est observé à travers une loupe ou un microscope. On appelle grossissement (noté G) le rapport G=a'/a Le microscope et son oculaire sont utilisés de façon intrinsèque (image instrumentale à l’infini), donc la puissance est intrinsèque est égale à : Pi = 4 G. Pi= D / ( f'1 f'2) ; D =21,4-1-4 = 16,4 cm = 0,164 m ; f'1 = 0,01 m et f'2 = 0,04 m Pi=0,164/(0,01*0,04)= 410 d. diamètre apparent de l'objet observé à la distance minimale de vision distincte dm=0,25 m : a = 4 10-6 / 0,25 = 1,6 10-5 rad Pi= 410 d d'où G= 410/4 = 102,5 = a' /a= soit a' = 102,5 a = 102,5*1,6 10-5 = 1,64 10-3 m. limite de résolution L= 0,61* 650 10-9 / 0,85 = 4,66 10-7 m.
l= h/(mv) = 6,62 10-34 / (9,1 10-31*1,68 108)= 4,33 10-12 m. limite de résolution théorique : L1= 0,61* 4,33 10-12 / 9 10-4 = 2,93 10-9 m. environ 100 fois plus grande que la limite de résolution du microscope optique : on pourra observer des objets 100 fois plus petits
|
||||
|
|