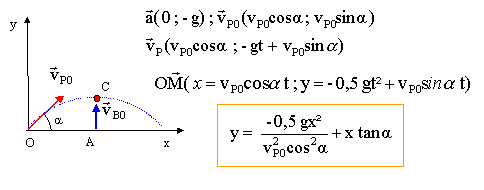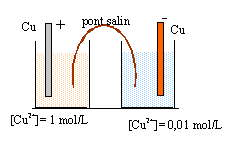|
- pile et électrolyse avec le cuivre (6,5 points) |
|||||||||||||||||||
|
|||||||||||||||||||
|
|
tir au pigeon : Le pigeon de masse mP=0,1 kg, assimilé à un point matériel M est lancé avec une vitesse initiale vP0=30 m/s, faisant un angle de 45° avec l'horizontale. Le tireur situé en A tire verticalement une balle de masse mB= 0,02 kg avec une vitesse initiale vB0= 500 m/s. La balle assimilée à un point matériel B part du point A tel que OA= 45 m. On donne g= 10 m/s². 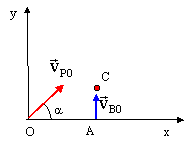
corrigé référentiel terrestre supposé galiléen ; systèmé étudié : le pigeon Le pigeon est soumis uniquement à son poids et en conséquence d'après la seconde loi de Newton, l'accélération est égale au vecteur g, verticale, orienté vers le bas.
Le vecteur vitesse est une primitive du vecteur accélération ; le vecteur position est une primitive du vecteur vitesse. On obtient la trajectoire en éliminant le temps. La trajectoire de la balle est la verticale passant par l'abscisse xC= 45 m et le point d'impact C est l'intersection de cette droite avec la parabole précédente. xC= vP0 cos a tC soit tC= xC/ (vP0 cos a ) = 45/(30*0,707)=2,12 s. la durée de vol est Dt = tC-t0 = 2,12 s. On néglige les forces s'exerçant sur la balle: le thèorème du centre d'inertie conduit à une accélération nulle. Le mouvement de la balle est rectiligne uniforme, suivant la verticale, à la vitesse constante vB0=500 m/s. durée du vol de la balle : Dt' = yC/vB0= 22/500 = 0,044s. cette valeur est très inférieure à Dt, durée de vol du pigeon et en conséquence le tireur peut viser directement le pigeon passant à sa verticale Si on ne néglige pas le poids de la balle, l'accélération de celle-ci est verticale vers le bas , de valeur g = 10 m/s².soit dans le repère d'étude ay = -10 m/s² ; ax=0. La vitesse est une primitive de l'accélération : vBy= vB0-gt' et vBx=0. valeur de la vitesse à la date t'=0,044 s : 500-10*0,044 = 500-0,44 = 499,56m/s. la vitesse de la balle varie très peu pendant le tir sur la distance de 22 m : on peut donc considérer la vitesse de la balle comme constante pendant la durée Dt=0,044 s.
|
||||||||||||||||||
|
Etude du carbone 14. Dans la nature le carbone 14 existe sous forme de deux noyaux isotopes 126C et 146C. Dans la haute atmosphère un neutron formé par l'action des rayons cosmiques bombarde un noyau d'azote 14 ( Z=7) qui se transforme en carbone 14 radioactif b- avec émission d'une autre particule.
Application à la datation : En 1983 fut découverte l'épave d'un drakkar dans la vase du port de Roskilde. Pour valider l'hypothèse indiquant que ce navire est d'origine Viking, une datation au carbone 14 est réalisée sur un échantillon de bois. L'activité d'un échantillon A(t) est de 12 désintégrations par minute et par gramme de carbone. Or l'activité pour 1 g de carbone participant au cycle du dioxyde de carbone de l'atmosphère est égale à A0= 13,6 désintégrations par minute.
corrigé A : nombre de masse ou nombre de nucléons du noyau. Z : numéro atomique ou nombre de charges ou nombre de protons du noyau. Le noyau de carbone 14 compte Z=6 protons et A= 14 nucléons : soit A-Z= 8 neutrons. Deux noyaux isotopes ne différent que par leur nombre de neutrons. Le noyau du
carbone 14 est radioactif : il se transforme spontanément au cours du
temps en émettant une particule et un rayonnement.
conservation du nombre de nucléons : 14+1 = 14 +A d'où A= 1 conservation de la charge : 7+0 = 6 + Z doù Z= 1 ( élément hydrogène) désintégration du carbone 14 : 146C = 147N + 0-1e temps de demi vie ou période : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. N(t) = N0 exp(-lt) avec N(t) : nombre de noyaux présents à la date t ; N0 : nombre de noyaux initiaux à a date t=0 ; l constante radioactive. ln 2 est un nombre sans dimension, la constante radioactive est donc l'inverse d'un temps. t1/2 s'exprime en année, l s'exprimera en année-1. l = ln 2 / 5570 =1,244 10-4 an-1. ou encore 1,244 10-4 / (365*24*3600) =3,94 10-12
s-1.
A(t) = A0 exp(-lt) soit ln[A/A0]= -lt ou ln[A0/A]= lt t = 1/l ln[A0/A] = 1/1,244 10-4 ln (13,6 /12) = 1005 ans. année de construction du bateau :1983 - 1005 = 978. L'hypothèse précédente est bien vérifiée. L'an 978 se situe dans l'intervalle : [700 ; 1000] ans.
|
|||||||||||||||||||
|
pile et électrolyse Cu : 63,5 g/mol ; e= 1,6 10-19 C ; NA= 6,02 1023 mol-1 ; F= 96500 C.
corrigé à l'anode négative, oxydation du cuivre métal de l'électrode : Cu(s)2 = Cu2+ (2) + 2e-. à la cathode positive, réduction des ions cuivre II : Cu2+ (1) + 2e- = Cu(s)1 bilan : Cu(s)2 +Cu2+ (1) = Cu2+ (2) + Cu(s)1 quotient initial Qr, i =[Cu2+ (2)] / [Cu2+ (1)]= 0,01 / 1 = 0,01 Qr, i < K donc évolution spontanée dans le sens direct, cohérent avec la polarité proposée.
A l'état d'équilibre : Qr, éq = K =1 d'où [Cu2+ (2)]éq = [Cu2+ (1)]éq A l'état d'équilibre, les concentrations en ions cuivre (II) dans les deux compartiments sont égales. 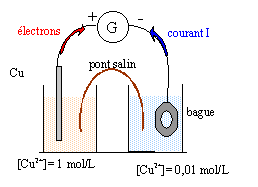
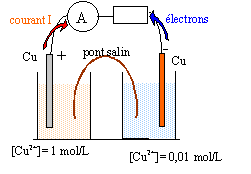
Le générateur force la réaction à évoluer en sens inverse. à l'anode positive, oxydation du cuivre métal de l'électrode : Cu(s)1 = Cu2+ (1) + 2e-. à la cathode négattive, réduction des ions cuivre II : Cu2+ (2) + 2e- = Cu(s)2 bilan : Cu(s)1 +Cu2+ (2) = Cu2+ (1) + Cu(s)2 Quantité d'électricité : Q = I Dt = 0,4*3600 = 1440 C La charge d'une mole d'électrons est, en valeur absolue égale à 96 500 C Qté de matière d'électrons : 1440/96500 = 0,015 mol. d'après Cu(s)1 = Cu2+ (1) + 2e- on déduit la qté de matière de cuivre : nCu= ½ne = ½*0,015 = 0,0075 mol Cu(s) soit en masse :
63,5*0,0075 = 0,47
g.
xf = ½n0 I2 + 2 S2O32- = 2I- + S4O62-. On ajoute quelques gouttes d'empois d'amidon dans le bécher contenant le diiode à doser. L'empois d'amidon est bleu foncé en présence de diiode ( ce dernier est en excès avant l'équivalence). Après l'équivalence le diiode est en défaut et l'empois d'amidon devient incolore. A l'équivalence, d'après les coefficients de l'équation de dosage : n(S2O32- ) versé = 2n1 n(S2O32- ) versé = volume (L) * concentration (mol/L) = 0,01*0,1 = 10-3 mol. n1 = 5 10-4 mol ; or n0 = 2n1 = 10-3 mol dans un volume V= 0,1 L C0=[Cu2+]= 10-3 / 0,1 = 10-2 mol/L.
|
|||||||||||||||||||
|
|