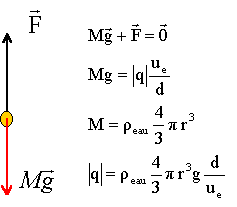|
- pile cuivre aluminium (2,5 points) |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
brouillard et vitesse : I- Modèle simple :Les gouttelettes qui se forment au
voisinage du sol sont de très petites dimensions ; nous allons
considérer l'évolution d'une goutte de brouillard sphérique, de rayon
r, de masse m, située à une altitude h du sol et soumise au seul champ
de pesanteur terrestre. On suppose la goutte immobile au début de
l'étude et on oriente l'axe vertical Oz vers le bas. L'origine est la
position initiale de la goutte.
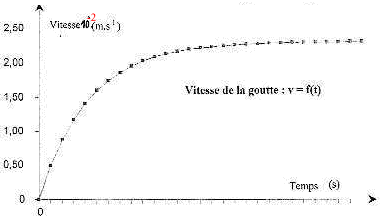
II- Frottements : en réalité la vitesse des gouutes à proximité du sol est constante et vaut vL= 2,3 10-2 m/s. Nous envisageons d'autres forces appliquée à la goutte, afin de se rapprocher des conditions réelles.
III- Brouillard simulé : Une lunette permet d'observer finement une zone située entre les armatures horizontales A et B d'un condensateur plan. L'armature supérieure est percée d'un orifice qui permet à l'opérateur de pulvériser un brouillard de fines gouttelettes entres les armatures. 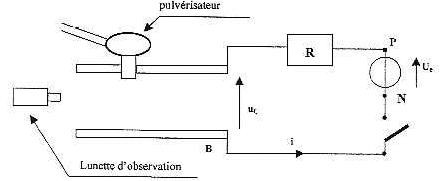
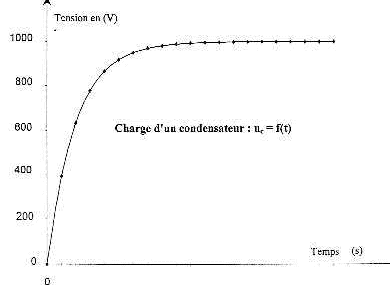
IV- Analogie mécanique- électrique : On constate que l'évolution temporelle du système électrique "condensateur" est analogue à celle d'un système mécanique " goutte de brouillard". En effet l'équation différentielle (1) peut être résolue anlytiquement et conduit à la solution v(t) = vL (1 - exp (-kt/m))
V- Brouillard stabilisé : Lorsque la tension aux bornes du condensateur est ue, toute particule porteuse d'une charge électrique q est soumise à une force électrique F, de direction perpendiculaire aux armatures, vérifiant l'expression F=que/d, "d" étant la distance des armatures. Lors de la pulvérisation des gouttes, celle -ci acquiert une charge électrique q négative. La lunette permet d'observer des gouttes dans leur mouvement de chute. Pour ue= 1000 V les gouttes sont immobiles.
corrigé Le champ de pesanteur terrestre est uniforme : direction verticale, sens vers le bas, valeur constante g=9,8 m/s². La seconde loi de Newton : la somme vectorielle des forces appliquées au système étudié est égale au produit de la masse M du système par le vecteur accélération du centre d'inertie du système. suivant l'axe Oz descendant dont l'origine est situé à l'altitude h=10 m. accélération a= g=9,8 m/s la vitesse est une primitive de l'accélération : v = gt = 9,8 t la position est une primitive de la vitesse : z=½gt² soit encore en éliminant le temps : t= v/g ; z=½g(v/g)² = ½v²/g soit v² = 2gz au sol : z=h=10 m ; v²sol = 2*9,8*10 = 196 ; v =14 m/s. poussée d'archimède = poids du volume d'air déplacé : P= rair Vg poids de la goutte : P= reau Vg or la masse volumique de l'eau est environ 700 fois plus grande que la masse volumique de l'air : la poussée est négligeable devant le poids. La seconde loi de Newton s'écrit suivant Oz : P-f = mdv/dt ; mg -kv = m dv/dt ; dv/dt = -k/m v +g. b est identifié à g et a est identifié à -k/m Lorsque la vitesse limite est atteinte : vL= constante ; dvL/dt =0 ; donc avL+b=0 ; vL= -b/a = mg/k. unité de k : force / vitesse soit masse * accélération / vitesse : [M] [L][T]-2[L]-1[T] = [M][T]-1 L'armature supérieure du condensateur est reliée à la borne positive du générateur : cette armature se charge positivement L'armature inférieure B, reliée à la borne négative du générateur porte une charge négative. i(t) = dq(t) / dt q(t) = C uC(t) avec C une constante donc i(t) = dq(t) / dt = CduC/dt additivité des tension uC + Ri = ue uC + R CduC/dt = ue. (2) dériver par rapport au temps uC(t) = ue (1-exp(-t/(RC)) duC/dt =ue/(RC) exp(-t/(RC) puis repport dans (2) : ue (1-exp(-t/(RC)) + RC ue/(RC) exp(-t/(RC) = ue. ue-ueexp(-t/(RC)) + ue exp(-t/(RC) = ue est vérifiée b- régime convergent : la valeur de la grandeur physique étudiée tend vers une valeur limite constante ; l'évolution du système présente deux phases distinctes : un régime transitoire et un régime permanent. t = RC ; uC(t) = ue (1-exp(-t/t ) pour la gouute de brouillard, la constante de temps vaut : t = m/k ; v(t) = vL (1 - exp (-t/t)) m/k est une masse divisée par (masse seconde -1) donc m/k s'exprime en seconde. les seules forces à prendre en compte sont le poids et la force électrique - la force de frottement f est proportionnelle à la vitesse et la vitesse est nulle donc f=0
|q|=103*4/3*3,14 * (5,4 10-6)3 *9,8 *0,1 / 103= 6,4 10-16 C. la force électrique et le champ électrique sont colinéaires et de sens contraire ( charge q négative) Le champ électrique pointe vers le bas, vers le plus petit potentiel: donc l'armature inférieure porte une charge négative.
|
||||||||||||||||||||||||
|
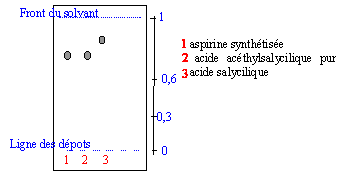
Contrôle de qualité sur l''aspirine synthétisée au laboratoire
corrigé 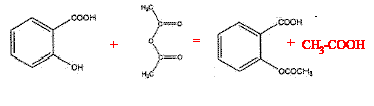
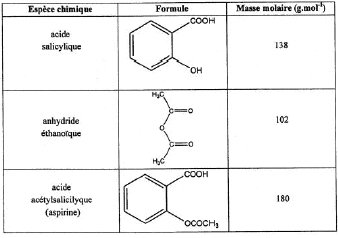
cette réaction est assez rapide, exothermique et totale l'acide sulfurique joue le rôle de catalyseur quantités de matière initiales des réactifs : anhydride éthanoïque : masse = masse volumique (g/mL) * volume (mL) = 1,08*15 = 16,2 g masse (g) / masse molaire (g/mol) = 16,2 / 102 = 0,159 mol. acide salicylique : masse (g) / masse molaire (g/mol) = 10/138 = 0,072 mol. la réaction s'effectue mole à mole, en conséquence l'acide salicylique est le réactif limitant. On peut espérer obtenir au plus 0,072 mol d'aspirine, soit en masse : 0,072*180 =13 g rendement de la synthèse : masse réelle / masse théorique calculée = 9,8 / 13 = 0,75 (75%) Rf=rapport frontal = distance parcourue par l'aspirine / distance parcourue par le solvant mesurer les distances sur le chromatogramme : Rf voisin de 0,75 / 1 = 0,75. Pou un éluant donné le composé synthétisé (1) et l'aspirine pur (2) possèdent le même rapport frontal ; en conséquence le composé (1) est identifiable à l'aspirine. Par contre dans le composé (1) il n'y a plus d'acide salicylique (3). AH +HO- = H2O + A-.
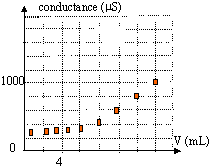
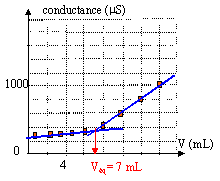
à l'équivalence les quantités de matière des réactifs sont en proportions stoéchiomètriques CaVa = CbVéq. Ca =CbVéq / Va = 0,1*7/100 = 7 10-3 mol/L soit 7 10-3 *0,25 = 1,75 10-3 mol d'aspirine dans S, donc dans le comprimé masse d'aspirine dans le comprimé : 1,75 10-3 *180 = 0,315 g. ce résultat était attendu puisque l'aspirine synthétisée était pure et la masse du comprimé était 0,32 g.
|
|||||||||||||||||||||||||
|
pile cuivre- aluminium Une pile est composée de deux demi-piles reliée par un pont salin. La première demi-pile est constituée d'une lame d'aluminium de masse m1= 1 g qui plonge dans 50 mL de solution de sulfate d'aluminium ( 2Al3+ et 3 SO42-) de concentration en ion aluminium 0,5 mol/L. La seconde est constituée d'une lame de cuivre de masse m2 = 8,9 g qui plong dans 50 mL de solution de sulfate de cuivre ( Cu2+ et SO42-) de concnetration en ion cuivre II égale à 0,5 mol/L. On associe à cette pile un ampèremètre et une résistance en série.
corrigé 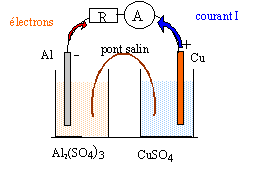
à l'anode négative, oxydation de l'aluminium: 2Al(s) = 2 Al3+ + 6e-. à la cathode positive, réduction des ions cuivre II : 3 Cu2+ + 6 e- = 3 Cu(s) 3Cu2+ + 2Al(s) = 2Al3+ + 3Cu(s). Qr, i
< K donc évolution spontanée dans le sens direct. ( évolution
cohérente)
Al : masse (g) / masse molaire (g/mol) = 1/27 = 0,037 mol Cu2+ : volume solution (L) * concentration (mol/L) = 0,05*0,5 =0,025 mol Cu ( produit) : 8,9 / 63,5 =0,14 mol Al3+
(produit) :
0,05*0,5 = 0,025
mol
si Al en défaut : 0,037-2xmax =0 soit xmax = 0,037/2 =1,85 10-2 mol. donc xmax= 8,3 10-3 mol. quantité maximale d'électricité que peut débiter cette pile : Qté de matière d'ion cuivre II : 0,025 mol d'après Cu2+ + 2 e- = Cu(s) à 2,5 10-2 mol d'ion Cu2+ il correspond 2*2,5 10-2 = 5 10-2 mol d'électrons Q= 5 10-2*96500 = 4825 C.
|
|||||||||||||||||||||||||
|
|