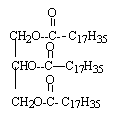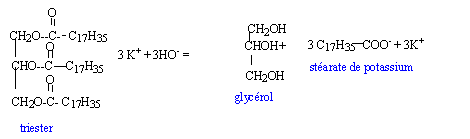|
Quand la cendre et le suif s'emmêlent...
Il y a quelques décennies, les femmes lavaient le linge au
lavoir en utilisant un mélange de suif (graisse animale) et de cendre.
On cherche à comprendre ici comment ces deux produits salissants
permettent le nettoyage.
- La cendre.
Les cendres étaient recueillies dans un pot et mélangées à de l'eau. La
cendre de bois contient de la potasse KOH. Sachant que la potasse
contient des ions potassium K+, écrire l'équation traduisant
la réaction associée à la dissolution de la potasse solide dans l'eau.
- Le suif.
Le suif est composé majoritairement de tristéarate (ou octadécanoate)
de glycéryle dont ta formule est :
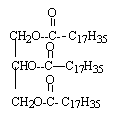
- A quelle famille chimique appartient le tristéarate de
glycéryle ? Recopier la formule et entourer les groupes
caractéristiques (ou fonctionnels) correspondant à cette famille.
- Donner la formule de l'acide (sans le nommer), ainsi que la formule
et le nom de l'alcool nécessaires pour fabriquer le tristéarate de
glycéryle. Comment se nomme cette réaction ?
- Le mélange de suif et de cendre...
- En utilisant les formules semi-développées, écrire l'équation
chimique de la réaction modélisant la transformation lors du mélange de
suif et de cendre.
- Par cette réaction, on obtient un savon qui a des propriétés
nettoyantes. Ce produit possède une partie hydrophile et une partie
lipophile. Identifier la partie hydrophile de l'ion négatif contenu
dans ce savon et préciser la définition du terme "hydrophile".
Principe de
fonctionnement d'un tube fluorescent
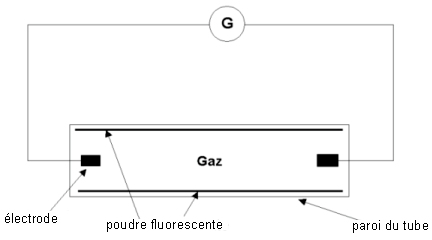
Le tube fluorescent étudié est constitué d'un cylindre de
verre qui contient un gaz à basse pression. La paroi intérieure du
cylindre est recouverte d'une poudre fluorescente. Lorsque le tube est
mis sous tension, une décharge électrique se produit : des électrons
circulent dans le gaz entre les deux électrodes. Les électrons
bombardent les atomes gazeux et leur cèdent de l'énergie.
Le schéma simplifié du circuit est donné ci-dessous :
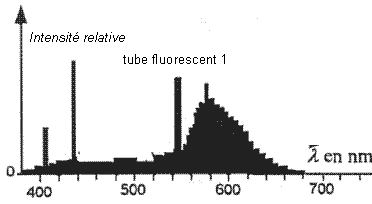
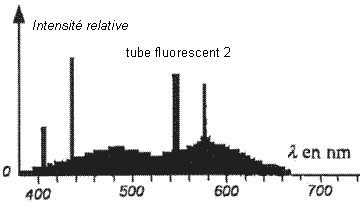
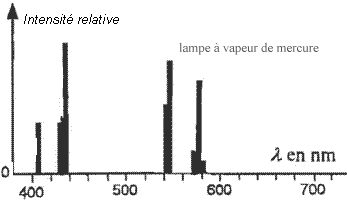
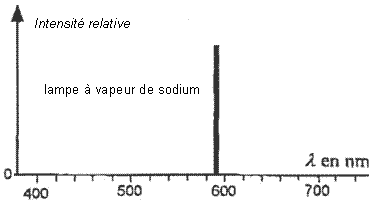
- On donne ci-dessous les spectres, dans le visible, des
lumières émises par deux tubes fluorescents et deux lampes (une lampe à
vapeur de mercure et une lampe à vapeur de sodium) vendus dans le
commerce.
- Quel est le gaz contenu dans les tubes 1 et 2 ? Justifier.
- Étude du spectre du mercure.
Le diagramme ci-dessous représente quelques niveaux d'énergie de
l'atome de mercure.
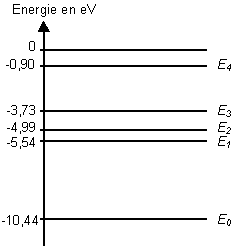
Comment désigne-t-on le niveau le plus bas E0
sur le diagramme énergétique ?
Un électron cède une partie de son énergie à un atome de mercure.
L'énergie de celui-ci passe du niveau E0 au niveau E1.
Comment qualifie-t-on l'état dans lequel se trouve alors l'atome de
mercure ?
- Retour vers E0.
Lors de la transition du niveau E1 vers le niveau E0,
l'atome de mercure perd un quantum d'énergie.
On donne : h = 6,63 10-34 S.I. ; c = 3,00 10 8 m.s-1
; 1 eV = 1,60 10-19 J.
Comment se manifeste cette perte d'énergie ?
Calculer la longueur d'onde l 1->0
correspondante dans le vide.
Après avoir rappelé les limites des longueurs d'onde dans le vide du
spectre visible, dire dans quel domaine, ultra-violet (U.V.), visible
ou infra-rouge (I.R.), se situe la radiation de longueur d'onde l 1->0
- Des U.V. à la lumière visible.
Pour que la poudre produise de la lumière visible, elle doit être
soumise à un rayonnement dont la longueur d'onde est comprise entre 200
nm et 300 nm. Elle émet alors de la lumière dont le spectre est continu.
-La vapeur de mercure contenue dans le tube permet-elle à la poudre
déposée sur les parois du tube d'émettre de la lumière visible ?
Justifier.
- Un éclairage confortable pour la restitution des couleurs correspond
à de la lumière dont le spectre est continu et se rapproche de celui de
la lumière solaire. En comparant les spectres des figures ci-dessus,
indiquer le rôle des poudres.
En comparant les spectres des figures 1 et 2 ci-dessus, montrer que la
nature de la poudre a une influence sur la couleur de la lumière émise.
corrigé
réaction associée à la dissolution de la
potasse solide dans l'eau.
KOH (s) =K+ + HO-.
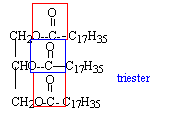
le tristéarate de glycéryle est un triester du glycérol CH2OH-CHOH-CH2OH
et de l'acide stéarique C17H35-COOH
la réaction du glycérol sur l'acide stéarique se nomme
estérification.
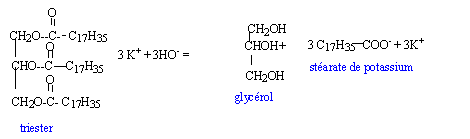
la partie hydrophile de l'ion négatif contenu dans ce savon
est constituée par la tête chargée électriquement -COO-.
définition du terme "hydrophile" : qui est ami de l'eau, qui a
une affinité pour l'eau
Sur les spectres des lumières
émises par les deux tubes fluorescents, les pics d'intensités relatives
sont les mêmes que ceux correspondant à la lampe à vapeur de mercure :
les raies d'émission, caractéristiques des éléments, sont donc
identiques.
Les deux tubes contiennent donc de la vapeur de mercure.
le niveau le plus bas est appelé niveau fondamental.
tous les autres états énergétiques sont des états excités
Si l'atome perd un quantum d'énergie, il y a émission d'un
photon, radiation lumineuse monochromatique.
longueur d'onde l 1->0
correspondante dans le vide :
énergie du photon émis : E= hc/ l 1->0 avec
E = E1-E0 = -5,54+10,44 = 4,9 eV
soit 4,9*1,6 10-19 = 7,84 10-19
J
l 1->0 = hc/E = 6,6 10-34*3
108 / 7,84 10-19 = 2,52 10-7 m = 252 nm.
Domaine des longueurs d'ondes du spectre visible : 380 nm à
780 nm
252 nm est une radiation du domaine ultra violet.
La radiation émise par la vapeur de mercure,
contenue dans le tube, a pour longueur d'onde = 252 nm, comprise donc
entre 200 et 300 nm. Soumise à ce rayonnement, la poudre fluorescente
déposée sur le tube va alors émettre de la lumière visible (dont le
spectre est continu).
Le spectre obtenu avec la lampe à vapeur de mercure seul
indique qu'il y a émission de quatre radiations monochromatiques
(spectre de raies).
Les spectres obtenus avec les tubes fluorescents indiquent
qu'il y a émission de toutes les radiations lumineuses de longueur
d'onde comprise entre 380 et 680 nm, s'ajoutant aux quatre radiations
correspondant à la vapeur de mercure (d'intensités plus fortes). Les
poudres fluorescentes permettent donc d'obtenir un spectre proche du
spectre continu obtenu avec la lumière solaire.
Sur le spectre 2, les radiations émises ont des intensités
relatives assez voisines, la lumière émise sera proche de la lumière
blanche solaire.
Sur le spectre 1, les intensités relatives augmentent
nettement entre 550 et 630 nm (avec un maximum vers 580 nm) ; la
lumière émise sera donc jaune-orangée.
|
|
L'aspirine
L'aspirine reste le médicament le plus consommé au monde.
L'aspirine peut se présenter sous de multiples formes
(comprimés simples ou effervescents, poudre soluble...), chacune
renfermant de l'acide acétylsalicylique, principe actif. Par la suite,
cet acide est noté AH et l'ion acétylsalicylate A-.
L 'exercice qui suit a pour but d'étudier le comportement de
la molécule AH en solution aqueuse. La réaction entre la molécule AH et
l'eau modélise la transformation étudiée.
Les parties 1. et 2. ont en commun le calcul de l'avancement
final de cette réaction par deux techniques différentes dont la
précision sera discutée dans la partie 3.
Données :
Conductivités molaires ioniques à 25 °C
|
Espèces chimiques
|
H3O+
|
HO-
|
A-
|
|
l en mS.m2.mol-1
|
35
|
19,9
|
3,6
|
pKa à 25 °C AH/A- : 3,5
Masse molaire moléculaire de l'acide acétylsalicylique AH : M
= 180 g.mol-1.
Par dissolution d'une masse précise d'acide acétylsalicylique
pur, on prépare un volume Vs = 500,0 mL d'une solution aqueuse d'acide
acétylsalicylique, notée S1 de concentration molaire en
soluté apporté cS = 5,55 10-3 mol.L-1.
- Etude de la transformation chimique par une mesure de pH. A
25 °C, la mesure du pH de la solution S à l'équilibre donne 2,9.
- Déterminer à l'équilibre, la concentration [H3O+]éq
en ions oxonium dans la solution S préparée.
- L'acide acétylsalicylique AH réagit avec l'eau. Ecrire l'équation de
la réaction modélisant cette transformation chimique.
- Déterminer l'avancement final xf de la réaction (on pourra
s'aider d'un tableau descriptif de révolution du système).
- Déterminer l'avancement maximal xmax de la réaction.
- Déterminer le taux d'avancement final t
de la réaction. La transformation étudiée est-elle totale ?
- Détermination de la constante d'équilibre de la réaction
par conductimétrie.
A 25 °C, on mesure la conductivité s de la
solution S à l 'aide d'un conductimètre. On obtient s = 44 mS.m-1.
Dans les conditions de l'expérience, on peut négliger la contribution
des ions HO- à la conductivité de la solution.
- Exprimer l'avancement final xf de la réaction entre
l'acide AH et l'eau en fonction de s , des
conductivités molaires ioniques utiles et du volume VS (on
pourra s'aider du tableau descriptif de l'évolution du système ).
- En déduire la valeur de xf.
- Calculer les concentrations molaires à l'équilibre des espèces AH, A-
et H3O+.
- Donner l'expression de la constante d'équilibre associée à l'équation
de la réaction entre l'acide AH et l'eau, puis la calculer.
- Précision des deux techniques utilisées : pH-mètrie et
conductimétrie. Le pH-mètre utilisé donne une valeur de pH précise à
O,1 unité de pH près, et le conductimètre donne une valeur de
conductivité précise à 1 mS.m-1 près. La valeur du pH est
donc comprise entre 2,8 et 3,0 et celle de la conductivité entre 43 mS.m-1
et 45 mS.m-1. Le tableau ci-dessous indique les valeurs de
l'avancement final de la réaction calculées pour ces différentes
valeurs de pH et de conductivité :
|
pH = 2,8
|
pH = 3,0
|
s = 43 mS.m-1
|
s = 45 mS.m-1
|
|
xf (en mol)
|
7,9 10-4
|
5 10-4
|
5,6 10-4
|
5,8 10-4
|
Conclure brièvement sur la précision des deux techniques, sans procéder
à un calcul d'erreur relative.
corrigé
[H3O+]éq
= 10-pH= 10-2,9 = 1,26 10-3 mol/L
AH + H2O = H3O+ + A-.
avancement final xf = [H3O+]éq
Vs = 1,26 10-3*0,5 = 6,3 10-4 mol
avancement maximal xmax=CsVs= 5,55 10-3*0,5
=2,77 10-3 mol
taux d'avancement final t = xf/xmax=6,3
10-4 /2,77 10-3 = 0,227.
valeur bien inférieure à 1: donc la transformation est
partielle.
conductivité s = l(H3O+[H3O+]éq+l(A-)[A-]éq avec
[H3O+]éq = [A-]éq
=xf/Vs
s =(l(H3O+
+ l(A-))xf / Vs soit
xf = s Vs / (l(H3O+
+ l(A-))
avec s = 44 10-3 S/m ;
Vs= 5 10-4 m3 ; (l(H3O+
+ l(A-)) = (35+3,6)10-3
S.m2.mol-1
xf = 44 10-3 *5 10-4 / 38,6
10-3 = 5,7 10-4 mol.
[H3O+]éq = [A-]éq
=xf /Vs = 5,7 10-4 / 0,5 = 1,14
10-3 mol/L.
conservation de A : [AH]éq + [A-]éq
=Cs = 5,55 10-3 mol/L
[AH]éq = 5,55 10-3 - 1,14 10-3
= 4,41 10-3 mol/L.
Ka = [A-]éq[H3O+]éq
/ [AH]éq = (1,14 10-3)2/4,41 10-3
= 2,94 10-4.
Précision des deux techniques utilisées : pH-métrie et
conductimétrie
D'après le tableau de données, c'est la méthode
conductimétrique la plus précise ; la valeur de l'avancement final se
situe dans un intervalle de largeur plus faible (0,2.10-4
mol en conductimétrie contre 2,9.10-4 mol en pH-métrie).
|
|
ballon sonde
Un ballon sonde, en caoutchouc mince très élastique, est
gonflé à l'hélium. Une nacelle attachée au ballon emporte du matériel
scientifique afin d'étudier la composition de l'atmosphère. En
montant, le ballon grossit car la pression atmosphérique diminue.
Sa paroi élastique finit par éclater à une altitude généralement
comprise entre 20 et 30 kilomètres. Après l'éclatement, un petit
parachute s'ouvre pour ramener la nacelle et son matériel scientifique
au sol. Il faut ensuite localiser la nacelle, puis la récupérer pour
exploiter l'ensemble des expériences embarquées.
Mécanique du vol
L'objectif de cette partie est d'étudier la mécanique du vol
du ballon sonde à faible altitude (sur les premières centaines de
mètres). On peut alors considérer que l'accélération de la pesanteur g,
le volume du ballon Vb et la masse volumique r de l'air restent
constantes. On modélisera la valeur de la force de frottement de l'air
sur le système étudié par l'expression :
f = K.rair .v² où K est
une constante pour les altitudes considérées et v la vitesse du centre
d'inertie du système {ballon + nacelle}.
On supposera qu'il n 'y a pas de vent (le mouvement s'effectue
dans la direction verticale) et que le volume de la nacelle est
négligeable par rapport au volume du ballon. Le système {ballon +
nacelle} est étudié dans un référentiel terrestre considéré comme
galiléen.
- Condition de décollage du ballon.
- Etablir le bilan des forces exercées sur le système {ballon +
nacelle}, lorsque le ballon vient juste de décoller. Indiquer le sens
et la direction de chaque force.
- La poussée d'Archimède. Donner l'expression littérale de la valeur FA
de la poussée d'Archimède.
Soit M la masse du système. Appliquer au système la seconde loi de
Newton (seule la relation vectorielle est demandée).
- La vitesse initiale du ballon (juste après le décollage) étant
considérée comme nulle, à quelle condition doit satisfaire le vecteur
accélération pour que le ballon puisse s'élever ? En déduire une
condition sur M
-. En déduire la masse maximale de matériel scientifique que l'on peut
embarquer dans la nacelle .
Données : rair = 1,22 kg.m-3
Vb = 9,0 m3 ; Masse du ballon (enveloppe +
hélium) : m = 2,10 kg ; Masse de la nacelle vide : m'= 0,50 kg
- Ascension du ballon. Montrer que l'équation différentielle
régissant le mouvement du ballon peut se mettre sous la forme : Av²+B=
dv/dt et donner les expressions de A et B. La masse de matériel
embarqué étant de 2,0 kg, l'application numérique donne A = -0,53 m-1
et B = 13,6 m.s-2.
- Une méthode de résolution numérique, la méthode d'Euler, permet de
calculer de façon approchée la vitesse instantanée du ballon à
différentes dates en utilisant la relation suivante :
v(tn+1) = v(tn) + D v(tn) avec D
v(tn) = a(tn)D t
tn+1 = tn + D t où D t est le pas de résolution.
- Par cette méthode on souhaite calculer la vitesse v1 à
l'instant de date t1 = 0,05 s et la vitesse v2 à
l'instant de date t2 = 0,1 s, la vitesse initiale du ballon
étant nulle. On prendra D t =0,05 s. En
utilisant la méthode d'Euler, l'équation différentielle et les valeurs
de A et B, recopier et compléter le tableau suivant :
|
Date t en s
|
Valeur de la vitesse en m./s
|
Valeur de l'accélération a en m./s²
|
D v(tn)
en m./s
|
|
t0=0
|
0
|
13,6
|
|
|
t=0,05
|
|
|
|
|
t=0,10
|
|
|
|
- Vitesse limite du ballon
- Donner l'expression littérale de la limite vl du ballon en
fonction de A et B.
- Calculer cette vitesse limite.
La méthode d'Euler donne le graphique suivant :
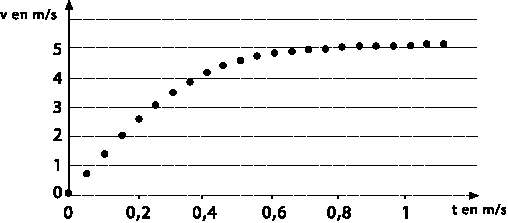
-Comparer la vitesse limite calculée à la valeur lue sur
le graphique (le calcul de l'écart relatif n'est pas demandé).
Le poids et la poussée d'Archimède
varient-ils avec l'altitude ?
Le tableau suivant donne quelques valeurs de grandeurs
mesurées au voisinage de la Terre.
|
Altitude h (m)
|
0
|
1000
|
2000
|
3000
|
4000
|
5000
|
6000
|
7000
|
8000
|
9000
|
|
Accélération de là pesanteur (m/s²)
|
9,8066
|
9,8036
|
9,8005
|
9,7974
|
9,7943
|
9,7912
|
9,7882
|
9,7851
|
9,7820
|
9,7789
|
|
Masse volumique de l'air( kg.m-3)
|
1,22
|
1,11
|
1
|
0,9
|
0,82
|
0,73
|
0,66
|
0,59
|
0,52
|
0,46
|
- Le poids.
En calculant l'écart relatif , montrer que pour les altitudes figurant
dans le tableau précédent, l'accélération de la pesanteur peut être
considérée comme constante à moins de 1 % près. On peut donc considérer
que le poids est constant entre les altitudes 0 m et 9 000 m.
- La poussée d'Archimède.
En s'aidant de la phrase soulignée dans l'introduction de l'exercice et
en considérant qualitativement l'évolution avec l'altitude de chaque
paramètre intervenant dans la poussée d'Archimède (dont la valeur est
notée FA), choisir et justifier la conclusion qui convient
parmi les propositions suivantes :
a- F augmente.
b- F reste constante
c- F diminue.
d- On ne peut pas conclure.
corrigé
Le système est soumis à 3 forces:
la poussée
d'Archimède, verticale, orientée vers le haut, valeur = poids du volume
de fluide (air) déplacé : F= rair Vb g
avec rair : masse volumique de l'air kg m-3
; Vb : volume du ballon (m3)
le poids du
système, verticale, orientée vers le bas, valeur : P= M g
la force de
frottement de l'air sur le système, verticale, orientée vers le bas,
valeur : f = K.rair .v² ( négligeable au début du
mouvement car la vitesse est alors très faible)
D'après la
seconde loi de Newton :
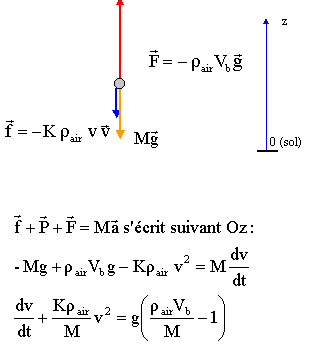
d'où par
identification : A
= - Krair /M et B = g (rair Vb /M-1).
Le ballon
s'élève si l'accélération est différente de zéro et orientée vers le
haut.
Or la vitesse
initiale étant négligeable, la force de frottement de l'air est
négligeable au moment du décollage.
d'où : F - P =
M.a ; rair Vb g
- M.g = M.a
a= (rair Vb / M-1)g positives
soit : M<rair Vb.
masse maximale
de matériel embarqué m" :
M = m + m' + m'',
m + m' + m'' < rair Vb ; m'' < rair Vb ; - (m + m').
La masse maximale
de matériel embarqué:
m" = 1,22 *9 -
2,1 - 0,50 = 8,38
kg.
méthode d'Euler :
v(tn+1) = v(tn) + D
v(tn) avec D v(tn) =
a(tn)D t
v(t1) = v(t0) + D
v(t0) avec D v(t0) =
a(t0)D t
D v(t0) = 13,6*0,05 =
0,68 m/s d'où v1=0+0,68 = 0,68 m/s
or l'équation différentielle donne : a(tn)= Av²(tn)
+B = -0,53 v² +13,6
a(t1) = - 0,53*0,682+13,6 = 13,35
m/s²
D v(t1)
= 13,35*0,05 = 0,668 m/s d'où v1=0,68 +0,668= 1,348 m/s
a(t2) = - 0,53*0,6682+13,35 =
13,11 m/s²
D v(t2)
= 13,11*0,05 = 0,668 m/s
|
Date t en s
|
Valeur de la vitesse en m./s
|
Valeur de l'accélération a en m./s²
|
D v(tn) en
m./s
|
|
t0=0
|
0
|
13,6
|
0,68
|
|
t=0,05
|
0,68
|
13,35
|
0,668
|
|
t=0,10
|
1,348
|
13,11
|
0,655
|
vitesse limite vl :
Lorsque la
vitesse limite est atteinte, le mouvement devient rectiligne uniforme
(l'accélération est nulle dvl/dt = 0)
l'équation
différentielle s'écrit : 0 = Av²l+B soit vl = (-B/A)½.
vl =
(-13,6 / (-0,53))½ = 25,66 ½ = 5,06 m/s.
D'après le graphe
la vitesse limite vaut environ 5,1 m.s-1. Ce résultat est en
accord avec la vitesse limite calculée.
Le poids et la poussée d'Archimède
varient-ils avec l'altitude?
(g9000-g0) / g0=
(9,7789- 9,8066) / 9,8066 = - 0,003 soit - 0,3%
donc
l'accélération de pesanteur peut être considérée comme constante à
moins de 1% près.
poussée : F= rair Vb g
g est considéré
comme constant; rair diminue mais Vb
augmente d'après le texte :
donc on ne peut
rien conclure quant à l'évolution de la valeur de la poussée ( réponse
d)
|