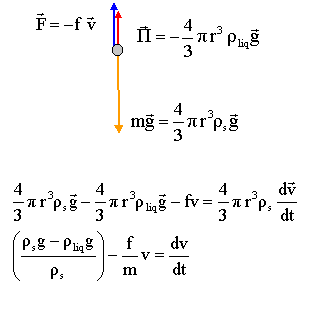|
- ondes (4 points) |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
but : expliquer, de façon simplifier, les processus mis en jeu lors de l'apparition d'une crampe pH du sang et maintien de sa valeur. Le sang peut être assimilé à une solution aqueuse ionique dont le pH ( valeur voisine de 7,4) est quasiment constant et ne peut subir que de faibles fluctuations. Le maintien de la valeur du pH se fait par deux processus : - Le premier met en oeuvre le couple acide base CO2, H2O / HCO3- ( pKa1 = 6,1 à 37°C) grâce à l'équilibre : CO2 + 2 H2O = HCO3- + H3O+ (1) - Le second processus est la respiration.
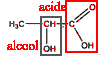
L'acide lactique : CH3-CHOH-COOH / CH3-CHOH-COO-.
Variation locale du pH du sang en l'absence de processus de maintien : Lorsque l'acide lactique produit dans la cellule musculaire est en partie transféré dans le sang, il réagit avec les ion s hydrogénocarbonate selon : CH3-CHOH-COOH + HCO3- = CH3-CHOH-COO- + CO2, H2O (3) A 37° pour le sang avant l'effort : [HCO3-]i=2,7 10-2 mol/L ; [CO2, H2O]i=1,4 10-3 mol/L ; pKa2 ( acide lactique / ion lactate) = 3,6. On considère un volume V= 100 mL de sang après l'effort dans lequel apparaît n0= 3 10-4 mol d'acide lactique.
corrigé Ka1 = [HCO3-][H3O+]/[CO2, H2O] log Ka1 = log [H3O+] + log [HCO3-]/[CO2, H2O] pKa1 = pH - log [HCO3-]/[CO2, H2O] pH= pKa1 +log [HCO3-]/[CO2, H2O] log [HCO3-]/[CO2, H2O] = pH- pKa1 =7,4-6,1 = 1,3 [HCO3-]/[CO2, H2O] = 10-1,3 = 0,05. Si [CO2, H2O] augmente alors le rapport [HCO3-]/[CO2, H2O] diminue et log [HCO3-]/[CO2, H2O] diminue or pH = pKa1 +log [HCO3-]/[CO2, H2O] , donc le pH du sang diminue. Au voisinage des poumons la quantité de O2 dissous augmente : l'équilibre (2) est déplacé vers la gauche, sens indirect, consommation de O2. Au voisinage des muscle la quantité de CO2 dissous augmente : l'équilibre (2) est déplacé vers la droite, sens direct, consommation de CO2. Lors d'un effort musculaire l'hémoglobine réagit avec CO2 en formant HBO2 : en conséquence [CO2, H2O] n'augmente pas et le pH du sang ne varie pas. Au niveau des poumons l'hémoglobine se charge en O2, libère CO2. Puis le flux sanguin amène HbO2 vers le muscle : celui-ci reçoit O2 et libère CO2 excédentaire. fonction alcool secondaire et fonction acide carboxylique en bout de chaine.
acide : espèce, ion ou molécule susceptible de céder un ou plusieurs protons H+. CH3-CHOH-COOH + H2O = CH3-CHOH-COO- + H3O+, transfert d'un proton à la molécule d'eau. CH3-CO-COOH + 2H+ + 2e- = CH3-CHOH-COOH. l'acide pyruvique, la forme oxydante du couple, se réduit en gagnant des électrons. ou bien on passe de la forme oxydante du couple à la forme réduite, l'acide lactique : donc réduction de l'acide pyruvique. 
si l'ion HCO3- est le réactif limitant : 2,7 10-3 -xmax =0 soit xmax = 2,7 10-3 mol On retient la plus petite valeur. [HCO3-]f = (2,7 10-3 - 3 10-4 )/0,1 =2,4 10-3 /0,1 = 2,4 10-2 mol/L [CO2, H2O]f = (1,4 10-4 +3 10-4) /0,1 = 4,4 10-4/0,1 = 4,4 10-3 mol/L. log [HCO3-]f / [CO2, H2O]f = log (24/4,4) = 0,737 pH= 6,1+0,737 = 6,84.
|
||||||||||||||||||||||||
|
Chute d'une particule dans un liquide visqueux. On prépare un mélange homogène constitué d'un liquide de masse volumique r1=1000 kg m-3 et de particules solides de forme sphérique de rayon R= 2 10-6 m, de masse volumique rs =1500 kg/m3 et de masse m= 4,5 10-14 kg. On dépose à la date t=0 une fine couche ( dont on néglige l'épaisseur ) de ce mélange homogène à la surface d'un récipient contenant le même liquide, à l'état pur, que le mélange précédent. Les particules que l'on suppose initialement au repos, se déplacent verticalement vers le fond du récipient. Les particules sont soumises: - à leur poids P, verticale vers la bas - à la poussée d'Archimède verticale vers le haut, de valeur 4/3pR3r1g. - à une force de frottement colinéaire à la vitesse et de sens contraire, de valeur F=f v avec f = 3,1 10-12 kg s-1. Pour l'étude l'axe Oz vertical est orienté vers le bas ; l'origine est la surface du liquide.
Modélisation simple d'un bac de décantation à flux horizontal. On fait circuler à vitesse vh un courant d'eau contenant des particules de masses différentes. En fonction des caractéristiques des particules, ces dernières vont tomber au fond du bac en des endroits différents. On peut ainsi séparer des particules de nature différentes. On s'intéresse au mouvement d'une particule ( identique à celle de la question précédente) initialement à la surface de l'eau, à la côte z=0 et pénétrant dans le bac en x=0. 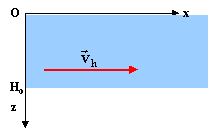
corrigé coefficient f = force / vitesse = masse * accélération / vitesse masse : [kg] ; accélération : [m] [s]-2 ; vitesse [m][s]-1. f : [kg][m] [s]-2 [s][m]-1 soit [kg][s]-1
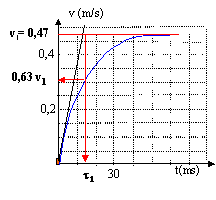
dv/dt + f/m v = g(1-r1/rs) la vitesse limite est atteinte vl = constante et alors dvl/dt=0 : f/m vl = g(1-r1/rs) ; vl=mg(1-r1/rs)/f. vl = 4,55 10-14 *9,8 ( 1-1/1,5) /3,1 1012 =0,47 m/s. 0,99 vl = vl (1- exp(-f/m t1)) 0,01 vl = exp(-f/m t1) ; ln (0,01 vl) = -f/m t1 ; t1 -m/f ln (0,01 vl)=4,5 10-14 / 3,1 10-12 ln (0,01 *0,47)=0,078 s = 78 ms.
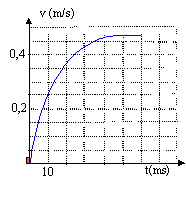
Le temps caractéristique est l'abscisse du point d'intersection de la tangente à la courbe à la date t = 0 s et de l'asymptote horizontale, t1 proche de 15 ms. régime transitoire ( si t <5*t1 ) durant lequel la vitesse augmente. au dela de 5*t1 , mouvement rectiligne uniforme ( vitesse limite atteinte) temps t2 mis pour parcourir la longueur du bac L=1 m à la vitesse de la circulation d'eau constante vh= 0,1 m/s: t2 =1/0,1 = 10 s. la vitesse limite de la chute verticale est atteinte au bout d'environ 5*0,015 = 0,075 s, valeur très inférieure à 10 s. La bille possède une vitesse verticale vz = vl très rapidement. Avec le courant d'eau, elle possède de plus une vitesse horizontale vh. Le vecteur vitesse de la bille est donc :
La trajectoire est une droite de coefficient directeur vl / vh avec vl = mg(1-r1/rs)/f. vl / vh = mg(1-r1/rs)/ (f vh ). valeur de la masse mc de la particule pour que
cette dernière tombe dans le bac de récupération au point de
coordonnées x=L et z= H0=0,54 m. 0,54 =mc g(1-r1/rs)/ (f vh ) soit mc = 0,54 f vh/ (g(1-r1/rs)) mc = 0,54*3,1 10-12*0,1 / (9,8(1-1/1,5)) = 5,1 10-14 kg. z(t) = vl x(t) / vh = mg(1-r1/rs)/ (f vh) x(t) z(t) est donc proportionnelle à la masse m. Si m < mC alors z(t) < H0 et la particule tombe après le bac de récupération. Si m > mC la particule tombe dans le bac de récupération.
|
|||||||||||||||||||||||||
|
Ondes
corrigé longueur d'onde (m) = célérité (m/s) / fréquence (Hz ) = 10/50 = 0,2 m. la fente étant horizontale, les taches de diffraction seront suivant la verticale.
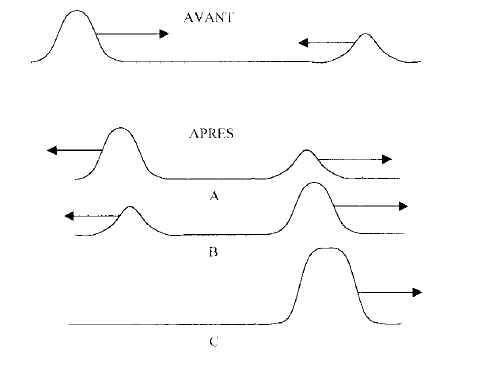
La fréquence de l'onde est indépendante du milieu de propagation., par contre la célérité et en conséquence la longueur d'onde dépendent du milieu : v= c/n ( c = 3 108 m/s) si l'indice augmente la célérité diminue ; l= v/f si v diminue alors la longueur d'onde diminue. Quand la température augmente, la célérité augmente. L'air n'étant pas un milieu dispersif pour le son, la célérité reste la même quelle que soit la fréquence. La célérité du son dans l'air est proche de 330 m/s ou voisine de 1000 km/h à 25°C. La perturbation de la surface de l'eau est transversale ; le flotteur oscille verticalement ( puis redevient immobile), il ne va donc pas se déplacer à la célérité v de l'onde ; l'onde se propage dans une direction horizontale. Une onde se propage sans transport de matière. La perturbation qui résulte du croisement des deux ondes est la somme géométrique des deux perturbations. Puis les ondes continuent à se propager sans avoir été modifiées par leur rencontre. C : somme géométrique des deux perturbations, mais pas au point de rencontre. A :est incohérent par rapport au sens de propagation initial. le cas B qui convient.
|
|||||||||||||||||||||||||
|
|