oxydo-réduction (7 points)- diagramme de solidification plomb étain ( 4 points)

- circuit en régime sinusoïdal (8 points)

d'après bac Sti génie des matériaux 2004




Google


oxydo-réduction :

potentiel standart à 298 K des couples oxydant / réducteur E0(Cu2+/Cu)= 0,34 V ; E0(H3O+/H2)= 0,0 V ;

E0(Zn2+/Zn)= -0,76 V ;

  1. Ecrire les demi-équations électroniques relatives à ces couples
  2. On réalise les expériences suivantes :
    - On plonge une lame de cuivre dans une solution d'acide chlorhydrique Y-a-t-il réaction ? Justifier.
    - On plonge une lame de zinc dans une solution d'acide chlorhydrique Y-a-t-il réaction ? Justifier.
    - Ecrire, quand il y a lieu, l'équation chimique en précisant l'oxydant et le réducteur.
  3. On réalise une pile standart ( les solutions ont un concentration de une mol/L) mettant en jeu les couples Cu2+/Cu et Zn2+/Zn
    - Compléter en l'annotant le schéma d'une telle pile
    - repérer le pole + de la pile et indiquer le sens de déplacement des électrons dans le circuit extérieur.
    - Donner l'expression littérale de la fem E de la pile dans les conditions standarts. Calculer E.
    seconde partie

On verse une masse m= 2,7 g d'aluminium dans un erlenmeyer contenant 600 mL d'une solution d'acide chlorhydrique telle que la concentration en ion oxonium soit 0,1 mol/L. L'équation chimique de la réaction qui se produit est :

6 H3O+ + 2Al(s) = 2 Al3+ + 3H2(g) + 6H2O

On donne la masse molaire de l'aluminium 27 g/mol

  1. Déterminer les quantité de matière en moles des réactifs mis en présence notées respectivement nAl et nH3O+.
  2. L'ion hydronium est le réactif limitant. Justifier.
  3. Montrer qu'il se forme 0,03 mol de dihydrogène.
  4. Déterminer le volume de dihydrogène dégagé sachant que le volume molaire des gaz est 24 L/mol.
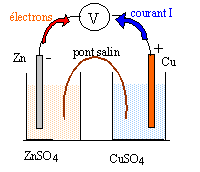
corrigé
Cu2++ 2e- = Cu(s)

2H3O++2e- = H2(g)+ 2H2O

Zn2++ 2e- =Zn(s)

On plonge une lame de cuivre dans une solution d'acide chlorhydrique :pas de réaction car le cuivre est un réducteur plus faible que H2.( ou bien l'ion Cu2+ est un oxydant plus fort que H3O+)

On plonge une lame de zinc dans une solution d'acide chlorhydrique : réaction car le zinc est un réducteur plus fort que H2.

Zn (s) + 2H3O+ = Zn2+ + H2(g) + 2H2O

le zinc est le réducteur, l'ion H3O+ est l'oxydant.

E= E0(Cu2+/Cu )- E0(Zn2+/Zn ) = 0,34-(-0,76) = 1,1 V

Qté de matère aluminium (mol) = masse (g) / masse molaire (g/mol) = 2,7/27 = 0,1 mol

Qté de matière ion oxonium (mol) = volume (L) * concentration (mol/L) = 0,6*0,1 = 0,06 mol

6 H3O+ + 2Al(s) = 2 Al3+ + 3H2(g) + 6H2O

D'après l'équation, à partir de 0,1 mol Al il faudrait 0,3 mol ion oxonium

or il n'y en a que 0,06 mol: Al en excès et ion oxonium en défaut.

à partir de nH3O+= 0,06 mol d'ion oxonium, les coefficients de l'équation indiquent qu'il se forme nH2 = ½ nH3O+=0,03 mol

soit en volume : 0,03*24 = 0,72 L H2.


Diagramme de solidification plomb étain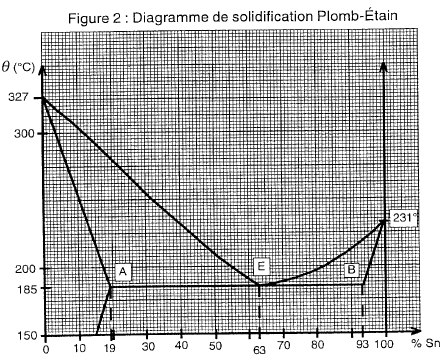

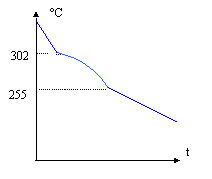
  1. Quelles sont les températures de début qd et de fin q f de solidification de l'alliage à 10 % d'étain ?
    - Tracer l'allure de la courbe de refroidissement q=f(t) de cet alliage.
  2. Quel est l'état physique de cet alliage à 10 % d'étain si la température est 200°C ?
    - Est-il homogène ou hétèrogène ?
    - Quel nom donne-t-on à cet alliage ?
  3. Comment s'appelle l'alliage à 63 % d'étain ?
    - Tracer l'allure de la courbe de refroidissement q=f(t) de cet alliage.
    - Calculer les pourcentages de ses deux phases homogènes à 184°C .
corrigé
températures de début qd = 302 °C et de fin de solidification q f = 255°C de l'alliage à 10 % d'étain

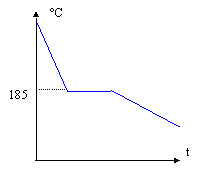
état physique de cet alliage à 10 % d'étain si la température est 200°C : solide, alliage homogène, solution solide.

l'alliage à 63 % d'étain : eutectique

l'eutectique à 184°C est constitué de solution solide d'étain à 19% et de solution solide d'étain à 93%.

On calcule les pourcentages de ces deux phases homogènes grâce à la règle des moments.

solution solide d'étain à 19% :EB/AB*100 = 30/74 *100 = 40,5%

solution solide d'étain à 93% : AE/AB*100 = 44/74*100 = 59,5%.

circuit en régime sinusoïdal

On place en série une résistance R, une bobine supposée parfaite d'inductance L et un condensateur de capacité C. Le dipôle ainsi constitué est alimenté sous une tension sinusoïdale u(t) fournie par un générateur basse fréquence. On appelle uR(t) la tension aux bornes de la résistance, uL(t) la tension aux bornes de la bobine, uC(t) la tensuion aux bornes du condensateur, i(t) l'intensité du courant.

  1. Faire le schéma du montage et inclure les appareils permettant de mesurer la valeur efficace U de u(t) et la valeur efficace I de i(t).
  2. La pulsation du signal u(t) est w= 1418 rad/s. Donner l'expression littérale liant la fréquence f et w.
    - Calculer f.
  3. Sachant que U= 24 V en déduire la valeur maximale de u(t).
  4. On choisit arbitrairement une phase à l'origine nulle pour la tension u(t). Ecrire l'expression de la tension instantanée u(t).
  5. Exprimer littéralement les impédances ZR, ZL et ZC des dipôles R, L et C.
    - Les calculer si R= 50 W, L=0,141 H et C= 4,70 mF.
  6. L'ampèremètre indique I= 340 mA. Donner l'expression de l'impédance Z de l'ensemble série (R L C) en fonction de U et I. calculer Z.
  7. Donner l'expression de la puissance perdue par effet joule PJ dans R. La calculer.
  8. Sachant que la puissance active P absorbée par l'ensemble (R L C) est égale à PJ, en déduire la valeur de P.
  9. Donner l'expression de la puissance apparente notée S absorbée par l'ensemble (R L C). Calculer S.
  10. Donner l'expression du facteur de puissance k du montage. Calculer k.
  11. Enoncer la condition de résonance de ce montage.
    - Calculer la valeur f0 de fa fréquence du signal u(t) permettant d'établir ce phénomène.
    - La valeur efficace de la tension u(t) étant toujours U = 24 V, calculer la valeur efficace I du courant à la résonance.

 

corrigé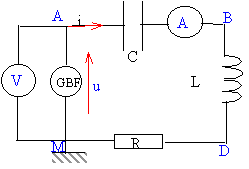

w=2pf soit f = 1418 / 6,28 =225 Hz.

valeur maximale de u(t) : Umax = U racine carrée (2) = 24*1,414 = 34 V.

u(t) = Umax cos (wt)

impédances ZR= R = 50 W

ZL = Lw = 0,141*1418 = 200 W

ZC = 1/(Cw) = 1/(4,7 10-6 *1418)= 150 W.

impédance de l'ensemble Z= U / I = 24/0,34 = 70,6 W.

puissance joule Pj= RI² = 50*0,34² = 5,78 W.

la puissance absorbée par l'ensemble est égale à la puissance joule.

puissance apparente S=UI= 24*0,34 = 8,16 VA.

facteur de puissance k= P/S= 5,78 / 8,16 = 0,71.

condition de résonance LCw0²=1

w0²= 1/(LC) = 1/(0,141*4,7 10-6) = 1,5 106

prendre la racine carrée w0 = 1,23 103 rad/s

f0 = 1,23 103 / (2*3,14) = 195,6 Hz.

à la résonance Z= R= 50 W

et Z= U/I d'où I= U/Z = 24 /50 = 0,48 A.

retour -menu