Aurélie nov 04

constante de raideur d'un ressort


Google



 

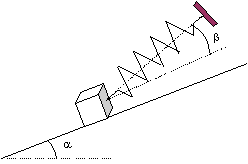
On attache l'une des extrémités du ressort à un cube d'arête a = 15,0 cm et de masse m = 3,50 kg ; l'autre extrémité du ressort est fixée à un support horizontal. On plonge totalement le solide dans un liquide de masse volumique r = 780 g.L-1 et on mesure l'allongement vertical x du ressort : x = 9,00 cm.

  1. Faire le schéma de l'expérience en y représentant sans soucis d'échelle les forces exercées sur le cube.
  2. Déterminer la valeur de la constante de raideur k du ressort.

 

corrigé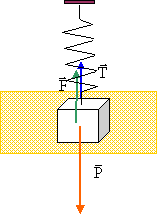

Le cube est en équilibre sous l'action de trois forces : le poids P=mg, vertical, vers le bas ;

la poussée d'Archimède F= rVcube g, verticale vers le haut

la tension du ressort T= k((l-l0) = kx, verticale, vers le haut.

A l'équilibre la somme vectorielle de ces trois forces est nulle.

P= F+T ; T=P-F ; kx= mg-rVcube g ; k= g(m-rVcube )/x.

avec m: masse du cube (kg) ; r: masse volumique du liquide kg m-3 ; Vcube ( m3) ; x: allongement du resort en m.

m= 3,5 kg ; r = 780 kg m-3 ; Vcube = (15 10-2)3 = 3,375 10-3 m3 ; x = 0,09 m.

k= 9,81(3,5-780* 3,375 10-3 )/ 0,09 = 94,5 N/m.


Le cube est à présent placé sur un plan incliné faisant avec l'horizontale un angle a = 40,0°. On l'accroche à l'une des extrémités du ressort, l'autre extrémité étant fixe. La direction du ressort et la pente forme un angle b = 20,0°. Le contact entre le plan incliné et le solide se fait avec frottements de valeurs f = 13,0 N. Le solide est en équilibre lorsque le ressort s'est allongé de x' = 10,2 cm.

  1. Représenter sur la figure ci-dessous, sans soucis d'échelle, les forces appliquées au solide.
  2. Déterminer la valeur de la constante k du ressort.
  3. Déterminer la valeur R de la réaction du support. Donnée : g = 9,81 N.kg-1.

 

corrigé

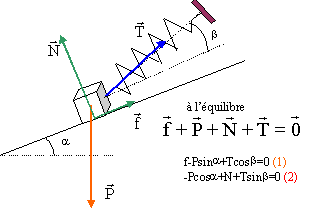
avec P= 3,5*9,81 =34,35 N ; T= kx' = 0,102 k ; f= 13 N ; a = 40,0° ; b = 20,0°.

(1) donne : T=(Psina-f)/cosb =(34,35*sin 40 - 13) / cos20 =9,08 /0,94 = 9,66 N

T= kx' donne k= T/x'= 9,66 / 0,102 = 94,7 N/m.

(2) donne : N= Pcos a -Tsinb = 34,35*cos40-9,66*sin20 =26,31-3,30 = 23 N.




retour -menu