1. Quel est le diamètre apparent d'un disque de diamètre 1 cm placé verticalement à 1,10 m d'un observateur ? Faire un schéma .
2. Sachant que ce diamètre apparent est approxivement le même que celui de la lune vue dela terre, en déduire le diamètre réel de la lune connaissant la distance terre lune (3,8410⁵ km).

---

corrigé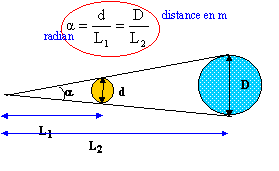

---

Le diamètre apparent d'un disque de diamètre 1 cm placé verticalement à 1,10 m d'un observateur est :

a = 0,01 / 1,10 = 9,1 10^-3 rad.

9,1 10^-3 = diamètre de la lune (km) / distance terre lune (km)

diamètre de la lune (km) =distance terre lune (km) * 9,1 10^-3 =3,84.10⁵ * 9,1 10^-3 = 3500 km.

---

Aristarque observe qu'au cours d'une éclipse de Soleil, la Lune cache exactement le Soleil. Or, il a déterminé que la distance qui le sépare du Soleil est égale à 20 fois la distance Terre-Lune. Il peut alors en déduire la valeur de R_s le rayon solaire... Données : diamètre apparent de la Lune : a = 0.52° = 9,07 10^-3 rad. estimation de la distance terre-lune : d= 4 10⁵ km^.

1. Donner l'ordre de grandeur de la distance terre soleil pour Aristarque.
2. Quelle est la valeur du diamètre apparent du Soleil ?
3. Faire un shéma de la situation. En déduire à un chiffre significatif près, le rayon du Soleil.
4. Rechercher la valeur du rayon R_s du Soleil. Comparer avecc la valeur d'Aristarque, en déduire où est l'erreur .

Un rayon lumineux traverse l'une des faces d'un cube en matière transparente sous une incidence de 45° puis rencontre une 2^è face perpendiculaire à la 1^ère. En admettant que le plan d'incidence soit normal à ces 2 faces et que le rayon sorte dans l'air en rasant la face de sortie, calculer l'indice de réfraction de la substance du cube. (Attention : sin (90° - r) = cos r) .

---

corrigé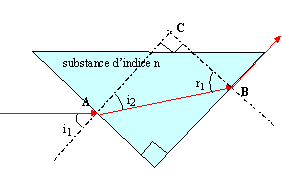

---

Le rayon entre sous incidence i₁=45°, est réfracté suivant un angle i₂

donc sin i₁= sin 45 = 0,707 = n sin i₂ (1)

puis attaque l'autre face suivant r₁ et ressort suivant un angle de 90° ; donc n sin r₁ = sin 90 = 1 (2)

Dans le triangle ABC rectangle en C : cos i₂ = sin r₁.

(2) s'écrit : n cos i₂ = 1

élever les relations au carré puis additionner : 0,707 ² = 0,5 = n² sin² i₂ ; 1= n² cos² i₂ .

0,5 + 1 = n²( sin² i₂ + cos² i₂ ) = n² ; n²= 1,5 soit n = 1,22.

---

On a un objet lumineux appelé point A dans l'eau, à une profondeur AH ( H projeté orthogonal de A sur le dioptre plan. L'objet A émet de la lumiere monochromatique les rayons émis se dirigent vers le dioptre plan eau-air que constitue la surface horizontale qui sépare les 2 milieux n _eau = 1.331 ; n _air = 1.000 ; n = n _eau / n _air. On appelle A' l'image du point A correspondant à un rayon incident AI .

1. Montrer , dans le cas général, que la relation entre HA, HA', les angles i et r s'écrit : HA'/HA = tan i / tanr .
2. Quel sont les conditions de gauss.
3. Etablir la relation donnant, dans l'approximation des petits angles, HA' ( dans les conditions de Gauss) en fonction de HA et de n
4. Que veut dire qu'un dioptre plan est un système optique non-stigmatique.

---

corrigé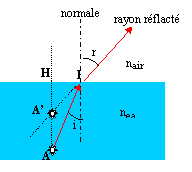

---

dans le triangle AIH : tan (AH, AI)= tan i = HI / AH

dans le triangle A'IH : tan (A'H, A'I)= tan r = HI / HA'

tan i / tan r = HA' / HA.

si les angles sont petits : tan i voisin de sin i proche de i radian et tan r voisin sin r proche de r radian

i/r = A'H / HA soit r/i = AH/A'H.

loi de la réfraction en I : n_eau sin i = n _air sin r

soit n = n_eau / n _air = sin r / sin i proche de r/ i ; n = r/ i.

donc n= AH/A'H soit A'H = AH/n.

dioptre plan : plan qui séparent 2 régions l'espace d'indice n différents.

conditions de Gauss : on prend des rayons qui font un angle très petit avec l'axe optique du diotre pour pouvoir approximer les tangentes (au voisinage de 0, tan a est environ égal à a radian)

système optique stigmatique : à tout point objet A corespond une unique image A'

donc système optique non stigmatique c'est l'inverse : à tout point objet A corespond plusieurs images distinctes.

On veut calculer la vitesse de la lumière dans le verre. Pour cela, on dispose d'un bloc cubique de 10 cm d'épaisseur. On envoie la lumière d'un laser sur ce bloc avec un angle d'incidence 80°. Le faisceau laser ressort du cube de verre à 8,7cm de la verticale du point d'entrée.

1. A partir d'une construction précise, mesurer au rapporteur l'angle de réfraction après la traversée de la surface de sépartion entre l'air et le verre.
   -En déduire l'indice de réfraction.
2. Calculer la valeur de la vitesse de la lumière dans ce bloc de verre.

---

corrigé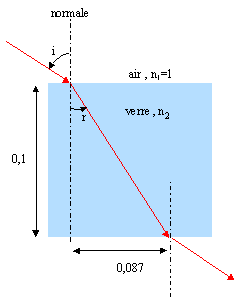

---

tan r = 0,087 / 0,1 = 0,87 ; r = 41°.

loi de Descartes pour la réfraction : n_air sin i = n_verre sin r.

sin 80 = n_verre sin 41 ; n_verre = sin 80 / sin 41 = 0,985 / 0,656 = 1,5.

L'indice de réfraction est égal au rapport de la vitesse de la lumière dans le vide 3 10⁸ m/s et dans le milieu transparent considéré.

n_verre = 3 10⁸ /v_verre ; v_verre = 3 10⁸ / n_verre = 3 10⁸ / 1,5 = 2 10⁸ m/s.

---

Une lentille convergente de distance focale OF'=50mm donne d'une tour, de hauteur AB=50 m, située à une distance de 250 m, une image A'B' nette sur un écran.

1. Quelle est la distance lentille écran ? Conclure.
2. Quelle est la taille de l'image de la tour sur l'écran ?
3. a est l'angle sous lequel est vu l'objet AB à l'oeil nu entre l'axe optique c'est à dire l'angle AOB. Calculer tan a , a en radians et a en degrés.