Aurélie nov 04

photométrie ; cellule photoélectrique ;

tube photomultiplicateur


Google



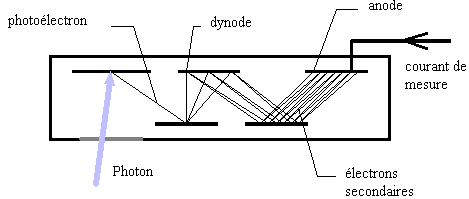
Comment peut-on extraire un électron d'un métal ?

Un métal est constitué par un réseau cristallin d'ions positifs fixes entre lesquels circulent des électrons libres de se déplacer à l'intérieur de ce réseau. Pour extraire un électron, il faut lui fournir une énergie Ws, appelée travail d'extraction. Une plaque de zinc est éclairée par la lumière émise par une lampe à vapeur de Hg, lumière riche en UV.

La lumière, éclairant la plaque de zinc, permet d'extraire des électrons du métal : c'est l'effet photoélectrique. L'effet photoélectrique est une interaction entre un photon et un électron.

Expliquer l'effet photoélectrique :

Il faut recourir au modèle corpusculaire de la lumière : un rayonnement électromagnétique de fréquence n peut être considéré comme un faisceau de particules : les photons. Chaque photon transporte l'énergie E = hn où h représente la constante de Planck.

Les propriétés du photon :

Sa masse au repos nulle. Sa charge électrique est nulle. Il se déplace dans le vide à la vitesse c = 3 ·108 m/s. Son énergie est : E = hn avec h = 6,62 10-34 Js. Or n =c/l.d'où E = hc/l avec l longueur d'onde ( en m) de l'onde électromagnétique associée au photon.

L'onde électromagnétique : elle est caractérisée par sa fréquence n (Hz) et sa puissance P éclairant une surface S.

P= Nhn / Dt où N est le nombre de photons frappant la surface pendant l’intervalle de temps Dt.

Seuil photoélectrique : Lors de l'interaction photon-électron , trois cas sont envisageables :

1) L'énergie du photon est égale au travail de sortie de l'électron . hn = Ws. L'énergie du photon suffit tout juste à expulser l'électron hors du métal. La fréquence du photon est égale à la fréquence de seuil du métal : ns = Ws/h.

2) L'énergie du photon est inférieure au travail de sortie hn < Ws. L'électron reste prisonnier du réseau métallique.

3) L'énergie du photon est supérieure au travail de sortie hn > Ws . Une partie de cette énergie sert à libérer l'électron du réseau métallique ; l'électron emporte l'excédent sous forme d'énergie cinétique Ec = hn - Ws .

Caractéristique d'une cellule photoélectrique : caractéristique courant-tension de la cellule photoélectrique pour une certaine puissance lumineuse.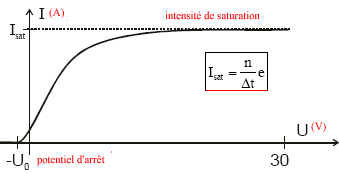

1. Si U augmente le nombre des électrons émis et qui atteignent le fil (qui circulent dans le circuit électrique) s'accroît.

2. Si U est supérieure à une certaine valeur, tous les électrons émis par la plaque atteignent le fil. Il en résulte dans le circuit une intensité de saturation Isat = n e/ Dt

où n est le nombre d'électrons émis pendant l’intervalle de temps D t et e = 1,6 10-19C, la charge élémentaire.

3. si U < -U0, aucun électron n'atteint le fil.

Plus la puissance lumineuse P reçue par la plaque est importante, plus l'intensité du courant de saturation Isat est grande. P n'a pas d'influence sur le potentiel d'arrêt U0.

La puissance lumineuse reçue dépend du nombre N de photons frappant la plaque pendant l'intervalle de temps D t. Pour une lumière monochromatique de fréquence n. P= Nhn/D t.

rendement quantique : Si au cours d’un certain intervalle de temps D t, N photons frappent la plaque, il y a n électrons éjectés. Le rapport h=n/N détermine la probabilité qu’a un photon d’interagir avec succès avec un électron. On l’appelle rendement quantique de la cellule.

Or N= PD t / (hn) et n = Isat D t/e d'où h= Isat hn / (Pe).


Les caractéristiques d'une lampe halogène sont : Pélectrique = 500 W ; Prayonnée = 300 W ; flux F== 7500 lm. Cette source suit :

- la loi de Stefan : P = s S T4 avec s = 5,67 10-8 W.m-2.K-4

- la loi de Wien : lmax T = 2,898 10-3 m.K.

  1. Est-ce une source lumineuse de type incandescence ou de type fluorescent ?
  2. Calculer son efficacité lumineuse et l'efficacité du rayonnement émis.
  3. Le filament a pour longueur l = 0,25 m et son diamètre est d = 0,1 mm. Calculer la température du filament lorsque la lampe éclaire.
  4. Calculer la longueur d'onde du rayonnement émis en plus grande quantité. Dans quel domaine se situe-t-il ?
  5. Cette lampe considérée comme ponctuelle est utilisée dans un luminaire qui répartit uniformément la lumière dans le demi-espace supérieur (éclairage indirect par réflexion sur le plafond). Calculer l'intensité lumineuse caractérisant cette source

 

corrigé :

de type incandescence

L'efficacité lumineuse exprime la quantité de lumière émise par une source pour un watt de puissance. Son unité est donc lm/W. 7500 / 500 = 15 lm/W.

surface du filament, surface latérale d'un cylindre S=lpd = 0,25*3,14*10-4 = 7,85 10-5 m²

La loi de Stephan détermine l'énergie totale du rayonnement émis : 300 = 5,67 10 -8 *7,85 10-5 T 4

d'où T 4 = 300 / (5,67 10 -8 *7,85 10-5) =6,7 1013 ; T= 2865 K

longueur d’onde du rayonnement émis en plus grande quantité ( loi de Wien)

lmax T = 2,898 10-3 ;lmax= 2,898 10-3 / 2865 = 1,011 10-6 m = 1011 nm ( domaine I.R)

flux total émis sur un plan : flux ( lumen) = 3,14 I ( candela)

I= 7500 / 3,14 = 2390 Cd.

Pour une cellule photoélectrique à vide poussé, on détermine l'intensité de saturation en fonction de la puissance rayonnante P captée par la cellule. On trouve :
P(mW)
2
4
6
8
Isat (mA)
2,73
5,46
8,20
11,0

  1. Que peut-on en conclure ?
  2. Cette cellule était éclairée pendant toute l'expérience par une radiation monochromatique l = 555 nm. Calculer le rendement quantique de la cellule.
  3. Le potentiel d'arrêt de cette cellule est 1 V. Calculer la vitesse maximale des électrons émis et le travail d'extraction des électrons.
 

corrigé :

Isat et P sont proportionnelles

 rendement quantique : n= n/N

n : nombre électrons émis en Dt seconde ; N nombre photons capturés en Dt s

n= I Dt / e avec e= 1,6 10-19 C

N= Poptique Dt / ( h n) avec h n = 6,6 10-34 * 3 10 8 / 555 10-9)=3,56 10-19 J

n = n/N= I hn / (Poptique e)=11 10-6*3,56 10-19 /(8 10-3 *1,6 10-19)=0,003.

travail d'extraction : e Uarrêt = 1,6 10-19*1 = 1,6 10-19 J

énergie du faisceau : h n = 3,56 10-19 J

énergie cinétique des électrons émis : (3,56-1,6 ) 10-19 = 1,96 10-19 J

vitesse : ½mv²= 1,96 10-19 avec m = 9 10-31 kg

v²= 2*1,96 10-19/ 9 10-31 = 4,35 1011

v= 6,6 105 m/s.

Le travail d'extraction d'un électron du zinc est WS = 3,3 eV.

  1. Calculer la fréquence seuil et la longueur d'onde seuil du zinc.
  2. On éclaire le zinc par une radiation UV de longueur d'onde l= 0,25 µm. Calculer l'énergie cinétique maximale de sortie des électrons et leur vitesse.
  3. On éclaire le zinc par la lumière d'un arc électrique en interposant une plaque de verre qui absorbe les ondes de longueur d'onde inférieure à 0,42 µm. Un effet photoélectrique est-il observé ?
 

corrigé :

fréquence seuil ns = Ws/h avecWS = 3,3 eV =3,3*1,6 10-19 J=5,28 10-19 J et h = 6,6 10-34 Js.

ns =5,28 10-19 /6,6 10-34 =8 1014 Hz.

longueur d'onde seuil dans le vide ls =c/ ns = 3 108 / 8 10-14=3,75 10-7 m = 375 nm.

énergie des photons de longueur d'onde l= 0,25 µm = 2,5 10-7 m.

E=hc/l =6,6 10-34 *3 108 / 2,5 10-7 =7,92 10-19 J

énergie cinétique des électrons émis : E-WS=7,92 10-19 -5,28 10-19 =2,64 10-19 J

½mv²= 2,64 10-19 avec m = 9 10-31 kg

v²= 2*2,64 10-19/ 9 10-31 = 5,86 1011

v= 7,6 105 m/s.

La longueur d'onde de seuil est 375 nm ; un effet photoélectrique est observé si la longueur d'onde de la lumière est inférieure à 375 nm. Dans le cas présent ( absence des radiations de longueur d'onde inférieure à 420 nm) il n'y a pas d'effet photoélectrique.


Une cellule photoélectrique possède une photocathode au césium. Elle est éclairée par une radiation monochromatique de longueur d'onde l = 0,425 µm. La puissance captée par la photocathode est P = 1 W. Les mesures donnent alors:

- intensité du courant de saturation Isat = 2 mA,

- potentiel d'arrêt U0 = 1 V.

Déterminer :

  1. La fréquence et l'énergie des photons incidents;
  2. L'énergie cinétique maximale de sortie des électrons photo-émis;
  3. La valeur du travail d'extraction Ws du césium;
  4. La fréquence et la longueur d'onde de seuil;
  5. Le nombre de photons captés par seconde;
  6. Le nombre d'électrons émis par seconde. Conclure.
 

corrigé :

La fréquence n et l'énergie E des photons incidents :

l = 0,425 µm= 4,25 10-7 m ; n = c/l = 3 108 /4,25 10-7 =7,06 1014 Hz.

E= hn = 6,6 10-34*7,06 1014= 4,67 10-19 J.

On utilise le théorème de l’énergie cinétique   EcA - EcC = travail de la force électrique + travail du poids.
Or le travail du poids de l’électron est négligeable par rapport au travail de la force électrique.

Le travail de la force électrique s'exprime par : q´UCA

D'où : EcA - EcC = q´UCA

Prenons le cas où UAC = - U0 : Dans ce cas particulier, les électrons sont freinés et ne peuvent pas atteindre l’anode A. On aura donc vA = 0 m.s-1 et donc EcA = 0 J.

De plus pour l’électron, on a q = -e. Donc 0 - EcC = (-e) ´ UCA = (-e) ´ (-UAC)

donc                -EcC = (-e) ´ (-(-U0)) = -e´U0          Finalement                  EcC = e´U0

A.N. : EcC = 1,6.10-19 ´ 1  = 1,6.10-19 J

On peut désormais utiliser la relation Ephot = WS + Ec e-  soit WS = Ephot - Ec e-
WS = 4,67.10-19 - 1,6.10-19 = 3,07.10-19 J  ou   1,92 eV

Fréquence et la longueur d'onde de seuil :

ns = Ws/h =3,07 10-19 / 6,62 10-34= 4,64 1014 Hz.

Longueur d'onde seuil dans le vide ls =c/ ns = 3 108 / 4,64 1014=6,46 10-7 m =646 nm.

nombre N de photons captés par seconde : P= Nhn/D t

N= PDt/(hn) =1*1/( 6,62 10-34 *4,64 1014 )=3,25 1018 photons.

nombre d'électrons émis par seconde : Isat = n e/ Dt

n= IsatDt/ e =2 10-3*1/1,6 10-19 =1,25 1016 électrons.

rendement quantique n/N=3,84 10-3.

La probabilité qu’a un photon d’interagir avec succès avec un électron est très faible.

Un tube photomultiplicateur comporte 16 dynodes. Chaque électron frappant une dynode provoque l’arrachement de trois électrons secondaires. La photocathode reçoit une puissance de 10-9 W sous la forme d’un rayonnement de fréquence 7 10 14 Hz. Sachant que le rendement quantique est de 1 %, calculer l’intensité du courant débité par le photomultiplicateur.

corrigé :

Nombre de photons frappant la cathode en 1 s. N= P/(hn) = 10-9 / (6,6 10-34*7 1014)= 2,16 109 photons

nombre d'électrons émis: n= rendement quantique fois nombre de photons n= 0,01 N = 2,16 107 électrons émis en 1 s.

nombre d'électrons secondaires émis par seconde après la dynode n°1 : n1 : 3*2,16 107= 6,5 107.

après la dynode n°2 : n2= 32*2,16 107= 1,94 108.

après la dynode n°3 : n3 = 33*2,16 107= 5,83 108.

après la dynode n°16 : n16 =316*2,16 107= 9,3 1014.

Intensité I = n16 e = 9,3 1014*1,6 10-19 =1,5 10-4 A


retour -menu