|
|
||||
|
||||
|
|
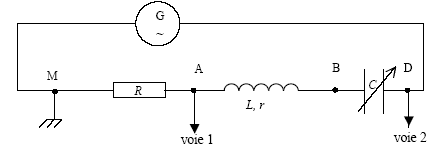
Le dipôle est constitué des éléments suivants associés en série : - Un conducteur ohmique R=8 ohms portant l'indication Imax = 0,75 A - Une bobine d'inductance L= 32 mH et de résistance r = 2 ohms portant l'indication Imax = 1,5 A. - Un concensateur de capacité C variable portant l'indication Umax= 350 V Il est alimenté par un générateur G délivrant la tension u(t) sinusoïdale : u(t) = Umax sin(wt)
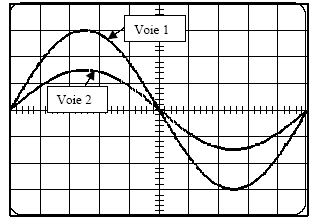
voie 2 :on visualise la tension uDM délivrée par le générateur, ou encore tension aux bornes du dipôle. période : 10 divisions soit 0,2*10 = 2 ms = 2 10-3 s. fréquence = 1/210-3 = 500 Hz. voie 1 : Umax : 6 V ; Ueff = 6/1,414 = 4,24 V d'ou Ieff = Ueff / R = 4,24 / 8 = 0,53 A. voie 2 : Umax = 7 V ; Ueff = 7/1,414 = 4,95 V. la tension aux bornes du dipôle et l'intensité sont en phase : on met en évidence le phénomène de résonance d'intensité. LC w0²=1 avec w0 = 2pf ; LC 4p² f ²=1. C= 1 / [4Lp² f ²]= 1/[4*0,032*3,14²*500²]=3,17 10-6 F = 3,17 mF. facteur de qualité Q= Lw/(R+r) = 0,032* 2*3,14*500/ (8+2)= 10. Q est élevé : la résonance est aigue, le circuit est sélectif. à la résonance d'intensité on observe une surtension aux bornes du condensateur égale à : UC= Q UDM = 10*4,95 = 49,5 V. Les trois éléments ont été correctement choisi car l'intensité qui les traverse est inférieure à Imax= 0,75 A et la tension aux bornes du condensateur est inférieure à Umax = 350 V.
|
|||
| |
||||
|
On désire contrôler le pH d'un milieu réactionnel afin que ce dernier soit maintenu voisin de 8. Il faut donc être averti par un signal lumineux de couleur différente selon que le pH est soit supérieur à 8 soit inférieur à 8. On a réaliser le circuit suivant : 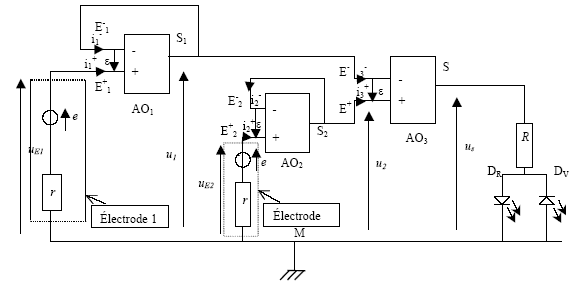 Une électrode de verre combinée, plongée dans une solution de pH donné est assimilée à une pile de f.e.m e et de résistance interne r telle que e= -0,058 pH+ 0,406 en V. L'électrode 1 plonge dans le milieu à contrôler, l'électrode 2 est dans la solution de référence de pHr=8,0. Les trois amplificateurs opérationnels sont idéaux et tels que Vsat = + ou - 14 V. DR et DV sont deux diodes électroluminescentes, respectivement rouge et verte, qui se comportent comme des diodes idéales.
corrigé AO idéal en régime linéaire : les intensités des courant d'entrées sont négligeables et la tenion e est nulle. uE1= e-r i1 avec e= -0,058 pH+0,406 er i1 = 0 courant d'entrée dans l'AO1 idéal uE1= -0,058 pH1+0,406 montage de l’AO1 : suiveur. en conséquence la tension d'entrée est égale à la tension de sortie. u1= uE1=
-0,058 pH1+0,406
uE2= -0,058 pHr+0,406 montage de l’AO2 : suiveur. en conséquence la tension d'entrée est égale à la tension de sortie. u2= uE2= -0,058 pHr+0,406 u2 = -0,058*8+0,406 = -0,058
V.
Dès que la tension d'entrée u1 est supérieure de quelque mV à la référence u2, le circuit délivre un niveau bas en sortie (-14 V). Au contraire, si la tension d'entrée u1 est inférieure de quelque mV à la référence u2, le circuit se met en fonction et nous trouvons un niveau haut (+14 V). si pH1 = 10 alors u1 = -0,058*10+0,406 = -0,174 V. u1<u2 donc US= +14 V La diode DR montée en direct est passante et DV
montée en inverse est bloquée u1>u2 donc US= -14 V La diode DV montée en direct est passante et DR
montée en inverse est bloquée
|
||||
|
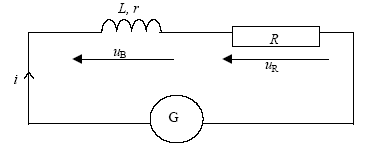
On réalise le circuit fermé ci-dessous : Ce circuit comporte : - un générateur G délivrant une tension sinusoïdale dont la valeur maximale est Um = 14,5 V ; - un conducteur ohmique de résistance R = 45 W ; - une bobine B d’inductance L et de résistance r. Pour analyser ce circuit, on utilise un oscilloscope bicourbe sur l’écran duquel on observe les tensions uB (voie 1) et uR (voie 2) représentées ci-dessous. 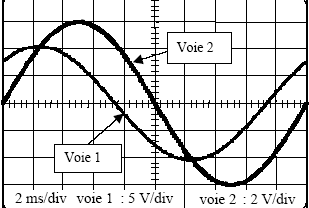
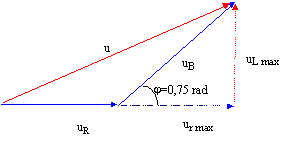
corrigé uR(t) est « l’image » de l’intensité du courant i(t) dans le circuit : la tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles. uR(t) = R i(t). période : 10 divvisions soit 10 *2 = 20 ms = 0,02 s. fréquence : f = 1/T= 1/0,02 = 50 Hz. La tension uR (voie2) donc l'intensité i(t) est en retard de1,2 divisions soit 1,2*2 = 2,4 ms sur la tension uB. 2,4ms correspond à 2,4/20 *2p= 0,75 rad= 43 °. uB max = 10 V ; UB eff = 10/1,414 =7,07 V. uR max = 6 V ; I max = uR max / R = 6 / 45 = 0,133 A I eff = 0,133/1,414 =0,095 A. impédance Z de la bobine : Z=UB eff /I eff = 75 W.
Ur max = uB cos 43= 7,31 V ; r = Ur max /I max =7,31/0,133 = 55 W. ULmax =uB sin 43= 6,81 V ; L=ULmax/ (2pf Imax) =6,81 / (2*3,14*50*0,133)=0,16 H. puissance active absorbée par la bobine rI²eff =55*0,095² =0,5 W puissance active absorbée par le résistor R : RI²eff =45*0,095² =0,4 W |
||||
|
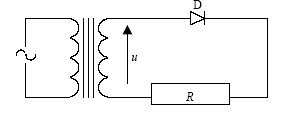
Le secondaire d’un transformateur délivre une tension u(t) de la forme : u(t) = 24*1,414 sin (100d t), en V.
corrigé 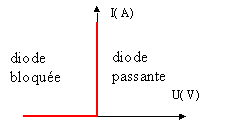
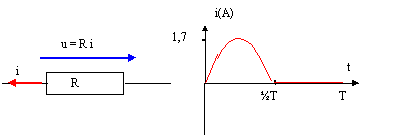
Montée en direct, la diode est pasante et la tension à ses bornes est nulle ( diode idéale) Par contre en inverse la diode se comporte comme un interrupteur ouvert. entre 0 et T/2 : diode passante u = Ri i(t) = u/R = 24*1,414 /20 sin (100d t) = 1,7 sin (100d t)
entre T/2 et T : diode non passante, i(t)=0 type de redressement mis en jeu : redressement monoalternance expression de uR(t) en fonction de u(t) et de E ( diode passante)
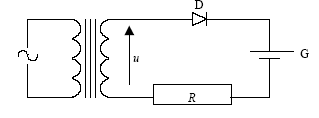
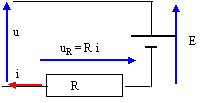
u= E+u R ; uR= u-E = 24*1,414 sin (100d t) -12 expression de i(t) : i (t)= (u-E )/R ; le courant circule dans la batterie si i(t) positif soit u(t) >E. valeur maximale de l’intensité du courant de charge i(t) : i(t) = 24*1,414/20 sin (100d t) -12/20 = 1,7 sin (100d t) - 0,6 valeur maximale si sin (100d t) = 1 soit Imax = 1,7-0,5 = 1,1 A.
|
||||
|
|