|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Sylvie a mal à la tête ; elle met un comprimé d'aspirine dans un grand verre d'eau. Après agitation elle s'aperçoit que des particules restent en suspension. Ce mélange non homogène n'étant pas agréable à boire, elle le filtre et boit le filtrat. Son mal de tête persistant elle se demande si elle a bien absorbé la totalité de l'aspirine contenue dans le comprimé, soit 500 mg. Données : la solubilité s en g/L d'une espèce A est la masse maximale de cette espèce que l'on peut dissoudre dans un mitre de solution à température donnée. La solution est saturée quand la valeur de la masse de soluté à introduire dans un litre de solution, à une température donnée, est supérieure ou égale à la valeur de s à cette température. La solubilité de l'acide acéthylsalicylique dans l'eau à 20 °C
est s= 3,3 g/L ; masse molaire acide acéthylsamicylique M= 180 g/mol.
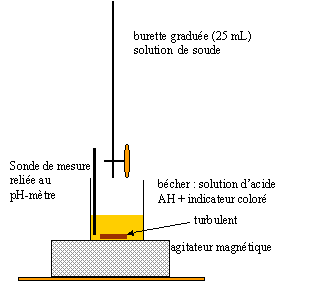
La transformation qui se produit lors du titrage est rapide et totale.
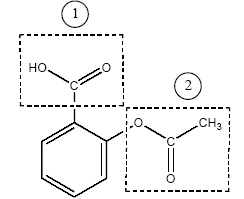
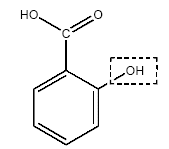
corrigé (1) : groupe ester et (2) groupe acide carboxylique.
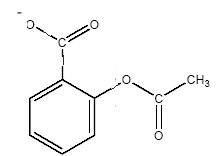
équation associée à la réaction chimique de titrage : AH + HO- = H2O + A-. l'ion acéthylsalicylate A l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoéchiométriques . CA VA = CB VBE soit CA =CB VBE / VA = 1,6 10-2*11,5/10 = 1,84 10-2 mol/L. La concentration massique Cm est égale à la concentration molaire (mol/L) fois la masse molaire de l'aspirine (g/mol) Cm = 1,84 10-2 *180 = 3,31 g/L Cette valeur étant supérieure à la solubilité s à 20°C, la solution S est saturée. Sylvie absorbe : 0,1 * 3,31 = 0,331 g soit 331 mg d'aspirine. Proposition 2 : V'BE = 11,5 mL ; le filtrat est toujours une solution saturée en acide acéthylsalicylique. saponification d'un ester : -OOC-C6H4-COO-CH3 + HO- = -OOC-C6H4-OH + CH3-COO-. on obtient l'ion salicylate et l'ion éhtanoate Lors du titrage de la solution S on n'a pas tenu compte de la saponification car cette réaction est très lente à 20°C ; de plus elle nécessite une solution de soude assez concentrée. on utilise l'anhydride éthanoïque CH3-CO-O-OC-CH3 HOOC-C6H4-OH + CH3-CO-O-OC-CH3 = HOOC-C6H4-COO-CH3 +CH3-COOH Un anhydride d'acide conduit à une réaction totale et rapide. Un acide carboxylique conduit à une réaction lente et limitée par l'hydrolyse de l'ester.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
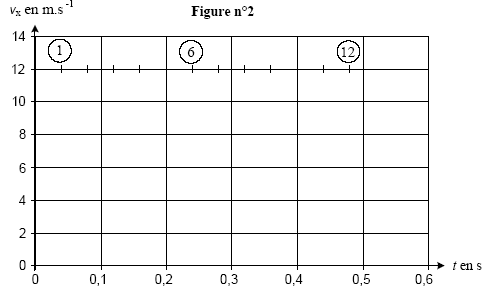
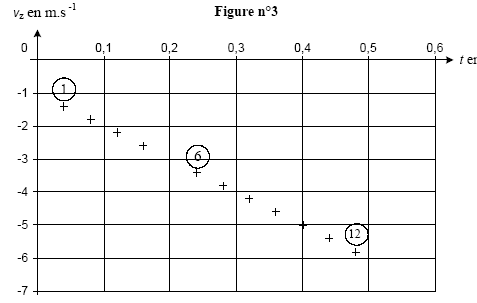
3On choisit sur le rivage une pierre plate et ronde, polie par le mouvement des flots, on la tient horizontalement entre les doigts puis, en s'inclinant le plus près possible du sol, on l'envoie sur la surface de l'eau. La pierre, animée d'une certaine vitesse glisse et nage à la surface ; lancée avec force elle saute et bondit en rasant les flots. Le vainqueur est celui dont la pierre est allée le plus loin et a rebondi le plus grand nombre de fois." Le reccord du monde officiel est de 38 ricochets. Données : g= 10 m/s² ; le référentiel terrestre est considéré galiléen. I Objectif : record du monde. La pierre utilisée de masse m= 0,10 kg est lancée d'un point A situé à une hauteur h au dessus de la surface de l'eau. Le mouvement est filmé à l'aide d'un caméscope dont l'axe de visée est horizontal et perpendiculaire au plan de la trajectoire. L'objectif du camescope est suffisamment éloigné de ce plan pour considérer que sa distance à la pierre est constante. Un logiciel de traitement d'images permet de visionner le film et de pointer les positions successives de coordonnées (x ; z) du centre d'inertie G de la pierre en fonction du numéro de l'image, donc à différents instants de date t. On obtient les résultats suivants : 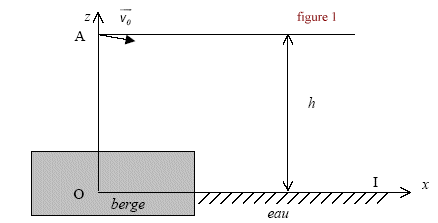
II Etude énergétique :
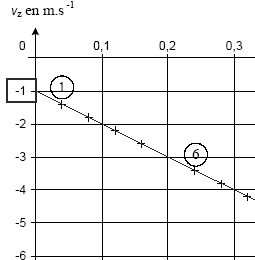
corrigé La pierre est soumise uniquement à son poids , vertical vers le bas ; en conséquence la composante horizontale de la vitesse initiale vx0 n'est pas modifiée : vx( t=0,08s) = 12 m/s. D'après le tableau toutes les 0,04 s la composante verticale de la vitesse diminue de 0,4 m/s : vz(t=0,08 s) = -1,8 m/s. vx0 = 12 m/s ; voz = -1 m/s ;
valeur v0 de la vitesse à l'instant de date t0=0: v0² = v²x0 + v²oz = 12²+(-1)²= 144+1=145 ; v0 =12,04 m/s. L'énergie mécanique est la somme des énergies potentielle de pesanteur et cinétique. Or l'altitude ne varie pas, l'énergie potentielle ne varie pas et la variation d'énergie mécanique correspond à la variation de l'énergie cinétique. DE= ½mv"²-½mv'²=½m(v"²-v'²)= 0,05(11²-13²)= 0,05(121-169)= -2,4 J. E(A) = mgh + ½mv0² E(A) = 0,1*10*1,75 + 0,5*0,1*12,04² = 1,75+0,05*145 = 9 J. A chaque rebond la pierre perd 2,4 J ; au bout de trois rebonds, l'énergie restante est 9-3*2,4 = 1,8 J Au quatrième choc avec l'eau la pierre ne rebondira pas. N= 3. La pierre est soumise à son poids, à la poussée d'Archimède due à l'air et à une force de frottement fluide proportionnelle à la vitesse ou au carré de la vitesse. Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps. ax= 0 car vx= constante az = coefficient directeur de la droite représentant vz en fonction du temps. az = -4/0,4 = -10 m/s. a² = ax²+az² = 0+10² soit a = g = 10 m/s². La seconde loi de newton indique que le vecteur accélération est proportionnel à la somme vectorielle. des forces appliquées à la pierre. Or la valeur de l'accélération est égale à g, donc le poids est prépondérant devant les autres forces. E(A) = 9 J ; E(I)= ½mv²' ; l'énergie mécanique se conserve entre A et I ½mv²'=9 soit v²' = 18/0,1 = 180 et v' = 13,4 m/s. Cette onde mécanique est transversale : la déformation du milieu s'effectue suivant la verticale alors que l'onde se propage suivant des directions horizontales. longueur d'onde (l (m)) = célérité (c (m/s)) fois période (T( s)) c = l / T avec l = 0,24 m ; T= 20*0,04 = 0,8 s c= 0,24 / 0,8 = 0,3 m/s.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I du chlore dans les eaux souterraines : il existe deux isotopes stables du chlore ( dont les nombre de masse sont 35 et 37) trouvés dans les proportions respectives de 3 pour 1 et qui donne aux atomes en vrac une masse molaire atomique apparente de 35,5 g/mol. Le chlore a neuf isotopes avec des nombres de masse s'étendant de 32 à 40 . Seulement trois de ces isotopes existent à l'état naturel : le Cl-35 stable ( 75,77 %), le Cl-37 stable ( 24,23 %) et le Cl-36 radioactif. Le rapport du nombre de noyaux de Cl-36 au nombre total de noyaux de Cl présents dans l'environnement est de 7,0 10-13 actuellement. Le Cl-36 se désintègre essentiellemnet en argon 36 ( Ar-36). La demi-vie du Cl-36 est de 301 103 ans. Cette valeur le rend approprié pour dater géologiquement les eaux souterraines sur une durée de soixante mille à un million d'années. Données : t½ l= ln2 ; A(t)= l N(t) ; 1 an = 3,156 107 s ; c= 2,998 108 m/s ; NA= 6,02 1023 mol-1 ;
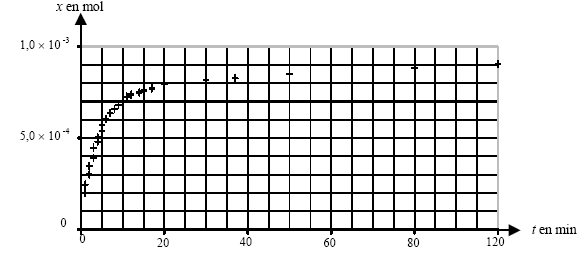
L'eau de Javel est une solution aqueuse contenant entre autres des ions hypochlorite ClO-(aq) et des ions chlorure Cl-(aq) Outre ses propriétés désinfectantes, l'eau de javel est utilisée comme agent blanchissant lié à l'action de l'ion hypochlorite sur de nombreux colorants. L'eau de Javel se décompose lentement selon une transformation totale modélisée par la réaction d'équation : 2 ClO-(aq) = 2 Cl-(aq) + O2 (g) réaction (1). On se propose d'étudier la décomposition d'une eau de Javel. On dilue la solution commerciale S0 pour obtenir un volume V=250 mL d'une solution S1 d'eau de Javel dix fois moins concentrée que S0. On verse V1 = 20 mL de S1 dans un ballon. A l'instant t0=0 s,où l'on déclenche le chronomètre, on ajoute sans variation de volume, une pointe de spatule de chlorure de cobalt dans la solution et on bouche le ballon. L'ion cobalt Co2+ est un catalyseur de la réaction (1). Pour suivre l'évolution de la transformation on mesure la pression p du gaz dans le ballon. La température T est maintenue constante et le volume V0 occupé par le gaz dans le ballon est constant. T= 296 K et V0 = 275 mL.
- fioles jaugées de 50 mL, 10 mL, 200 mL, 250 mL, 500 mL - pipettes jaugées de 5 mL, 10 mL, 20 mL, 25 mL - pipettes graduées de 5 mL, 10 mL, 20 mL, 25 mL - éprouvettes graduées de 10 mL, 20 mL, 250 mL, 500 mL
corrigé Les valeurs 35 et 37 indiquent le nombre de nucléons ( protons et neutrons) que comptent les noyaux de Cl-35 et Cl-37. De plus Z=17 donc Cl-35 compte 17 protons et 35-17 = 18 neutrons Cl-37 compte 17 protons et 37-17 = 20 neutrons. Deux isotopes ne se différentient que par leur nombre de neutrons. 3617Cl : 17 protons et 36-17 = 19 neutrons. Energie de liaison ELi d'un noyau de "chlore 36" : |Dm|=(59,711 28 -17* 1,672 62-19*1,674 92) 10-27=0,546 74 10-27 kg énergie associée à cette perte de masse : E= |Dm| c² = 0,546 74 10-27 *(2,998 108)2=4,9141 10-11 J soit en eV : 4,9141 10-11 / 1,602 10-19 = 3,067 108 eV = 306,7 MeV. 3617Cl -->3618Ar + 0-1e : radioactivité b-. conservation de la charge : 17 = 18 -1 conservation du nombre de nucléon : 36 = 36 +0. Le temps de demi-vie t½ est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. t½ l= ln2 ; ln2 est sans dimension, en conséquence la constante radioactive est l'inverse d'un temps ( s-1) t½ = 301 103 * 3,156 107 =9,499 1012 s l= ln2 / 9,499 1012 = 7,297 10-14 s-1. 13,5 10-3 g dans 1 L soit 13,5 10-3*1,5 = 2,025 10-2 g d'ion chlorure dans la bouteille Qté de matière (mol) = masse (g) / masse molaire (g/mol) = 2,025 10-2 / 35,5 = 5,704 10-4 mol. nombre d'ion chlorure : 5,704 10-4 / NA = 5,704 10-4 * 6,02 1023 =3,434 1020 ions nombre de noyaux de chlore 36 : N= 3,434 1020 * 7,0 10-13 =2,4 108. activité A= l N= 7,297 10-14*2,4 108 = 1,754 10-5 Bq.( désintégrations par seconde) un jour = 24*3600 s = 8,64 104 s. nombre moyen de désintégrations par jour : 8,64 104* 1,754 10-5 = 1,5 . Loi de décroissance radioactive : N(t) = N0 exp (-lt) N(t) / N0 =0,38 = exp (-lt) avecl= 7,297 10-14 s-1. ln 0,38 = -lt ; t = ln 0,38 /( -l)= -0,9676 / (-7,297 10-14 )=1,326 1013 s 1,326 1013 / 3,156 107 =4,2 104 ans= 420 103 ans. Cet âge est très supérieur ( environ 70 fois plus ) au temps de demi-vie du "carbone 14" : la méthode de datation au "carbone 14" serait très imprécise du fait que ce dernier aurait pratiquement totalement disparu à cette date. V=250 mL d'une solution S1 d'eau de Javel dix fois moins concentrée que S0. Donc fiole jaugée de 250 mL et pipette jaugée de 25 mL
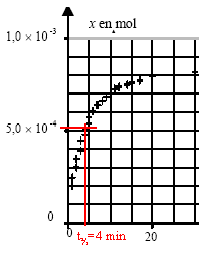
x(t1)= [(1084-1020)*102]*275 10-6 / ( 8,314 * 296) = 7,15 10-4 mol. Vitesse v(t) de la réaction : v(t) = 1/V dx(t) / dt avec V volume de la solution et x(t) avancement . graphiquement la vitesse est proportionnelle au coefficient directeur de la tangente, à une date donnée, à la courbe x(t). Au début la tangente est presque verticale, puis elle s'incline de plus en plus sur l'horizontale : son coefficient directeur diminue de plus en plus. La vitesse de la réaction diminue au cours du temps car la concentration du réactif diminue. Le temps de demi-réaction est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final x(t½) = 5 10-4 mol.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||