|
|
||||
|
||||
|
|
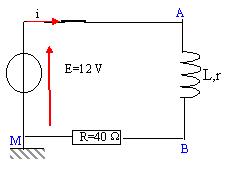
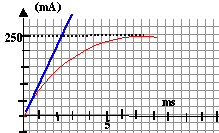
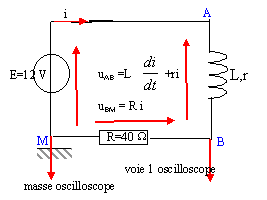
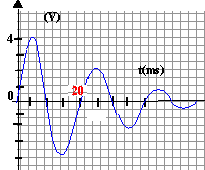
La tension aux bornes d'un résistor est proportionnelle à l'intensité du courant qui le traverse : visualiser uBM, c'est visualiser l'image de l'intensité au facteur R= 40 près. Il suffit ensuite de diviser les valeurs lues sur l'oscilloscope par 40 pour obtenir les valeurs de l'intensité en A.
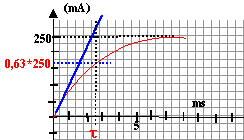
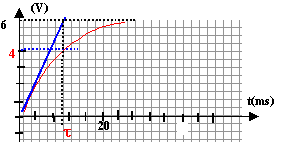
Tracer l'asymptote et la tangente à l'origine : leur intersection donne en abscisse la valeur de t. t voisin de 2,5 ms soit 2,5 10-3 s. ou bien à t = t , l'intensité est égale à 0,63 fois la valeur maximale. t = L / (R+r) soit L =t(R+r) = 2,5 10-3 *(40+8)=0,12 H.
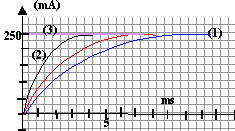
(1) si L augmente t croît. (2) si r augmente t décroît. (3) bobine remplacée par un résistor de résistance r.
|
|||
|
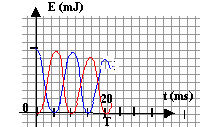
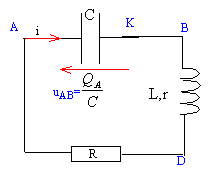
On considère un montage contenant en série : un condensateur de capacité C = 10 mF, une bobine d'inductance L = 0,9 H un interrupteur K et une résistance variable R. L'interrupteur étant ouvert, l'armature A du condensateur porte la charge QA =4 10-5 C. A la date t = 0 on ferme l'interrupteur.
tension aux bornes du condensateur : uAB= QA/C=4 10-5 / 10 10-6 = 4 V. si R= 0 , régime périodique sinusoïdal si R faible, régime pseudopériodique (1) si R grand, régime apériodique (2) la pseudopériode T est voisine de 20 ms = 2 10-2 s. période propre : T0 = 2p (LC)½ = 2*3,14 (0,9*10-5)½=18,8 10-3 s = 18,8 ms. aspect énergétique : courbe bleue : énergie stockée dans le condensateur ; initialement ( t=0) la tension aux bornes du condensateur est maximale, ce dernier stocke toute l'énergie du dipôle RLC courbe rouge : énergie stockée dans la bobine ; initialement l'intensité est nulle et la bobine ne stocke pas d'énergie. Au cours du temps l'énergie diminue : lors des échanges d'énergie entre bobine et condensateur, une partie est perdue par effet joule dans les résistances.
|
||||
|
A l'instant initial le condensateur C est déchargé. On ferme alors l'interrupteur K. R= 1 kW. 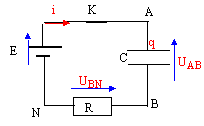
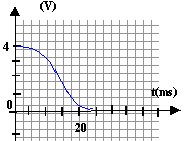
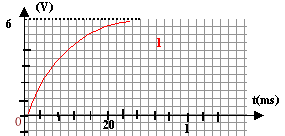
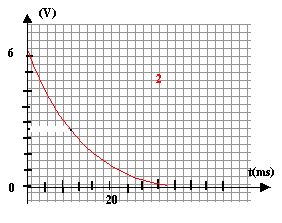
corrigé Aux bornes d'appareils en série, les tensions s'ajoutent : E= UAB + UBN. A l'instant initial le condensateur C est déchargé : la tension à ces bornes est nulle, puis va croître jusqu' à la valeur 6 V ( courbe 1) La courbe 2 correspond à la tension aux bornes du résistor. la tension E vaut 6 V, tension aux bornes du condensateur complètement chargé.
Tracer l'asymptote et la tangente à l'origine : leur intersection donne en abscisse la valeur de t. t voisin de 10 ms soit 10-2 s. ou bien à t = t , la tension est égale à 0,63 fois la valeur maximale. t= RC avec R= 1000 W d'où C=t/ R = 10-2/1000 = 10-5 F = 10 mF. |
||||
|
|