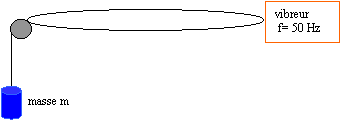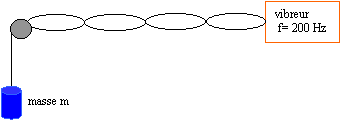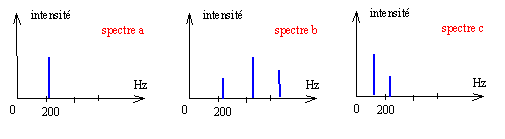
Aurélie sept 04

ondes stationnaires

exercices type oral bac



Google



guitare

 L'une des cordes de guitare permet de jouer le La2 de fréquence associée 220 Hz. On enregistre le spectre en fréquence.

  1. Quel est le spectre correspondant ? Justifier.
  2. La corde de guitare en y faisant circuler un courant sinusoïdal ; on obtient des oscillations entretenues de fréquence 220 Hz. Sur le schéma de l'expérience ci-dessous, il manque un objet essentiel pour observer convenablement l'aspect particulier pris par la corde.

    - Lequel ?
    - Comment faut-il le placer pour obtenir une grande amplitude du phénomène observé ?
    - Dessiner l'aspect de la corde en notant la position des nœud(s) et ventre(s) de vibration.

  3. La distance séparant le chevalet du sillet est égale à 65 cm. Calculer la longueur d'onde l de l'onde progressive sinusoïdale créée le long de la corde.
  4. En déduire la célérité de l'onde le long de cette corde.
  5. De quelles grandeurs dépend cette célérité ? Expliquer alors pourquoi il faut agir sur les chevilles pour accorder une guitare. 

corrigé
Le son émis par la guitare n'est pas un son pur ( un son émis par un diapason est pur) ; en conséquence le spectre contient le fondamental et plusieurs harmoniques de fréqences multiples de la fréqence du fondamental 220 Hz. ( spectre b)

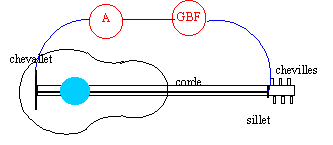
Pour observer convenablement l'aspect particulier pris par la corde il faut ajouter un aimant en forme de fer à cheval ; la corde de guitare doit passer entre les branches de l'aimant ( se trouver dans l'entrefer de l'aimant). On observera un phénomène de grande amplitude si la position de l'aimant correspond à la position d'un ventre de vibration.

Le GBF délivre un signal de fréquence 220 Hz, égale à celle du fondamental : on observera donc un seul fuseau ; en conséquence l'aimant sera placé au centre de la corde.

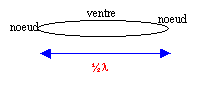
La distance séparant deux noeuds consécutifs étant ½ l , la longueur d'onde vaut : 2*0,65 = 1,3 m.

célérité v (m/s), longueur d'onde l (m) et fréquence f (Hz) sont liées par la relation

l = v/f soit v = lf =1,3*220 = 286 m/s.

La célérité dépend de la tension de la corde, de la nature du métal constituant la corde. En agissant sur les chevilles on modifie la tension de la corde, donc la célérité ; or la longueur de la corde étant constante, agir sur les chevilles, c'est modifier la fréquence du fondamental, et en conséquence accorder la guitare.


ondes stationnaires

Une corde ( longueur L=1m) dont l'extrémité E est reliée à un vibreur, est tendue, après passage sur une poulie, par une masse m.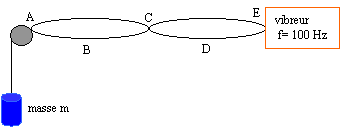

 

  1. Nommer les points A, B, C, D et E.
  2. Quelle est la longueur d'onde.
  3. Calculer la célérité de l'onde dans la corde.
  4. Dessiner l'aspect de la corde lorsque f = 50 Hz. Comment se nomme ce mode de vibration ?
  5. Dessiner l'aspect de la corde lorsque f = 200 Hz. Comment se nomme ce mode de vibration ?
     
corrigé
A, C et E sont des noeuds de vibration

B et D sont des ventres de vibration.

La distance séparant deux noeuds consécutifs étant ½ l , la longueur d'onde vaut : 1 m.

célérité v (m/s), longueur d'onde l (m) et fréquence f (Hz) sont liées par la relation

l = v/f soit v = lf =1*100 =100 m/s.

mode correspondant à la fréquence du fondamental ( f0= 50 Hz)

mode correspondant à la fréquence de l'harmonique de rang n= 4 ( f = 4 f0 = 4 *50 Hz)

retour -menu