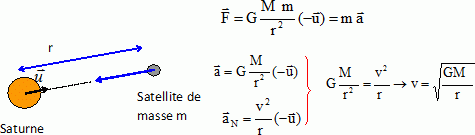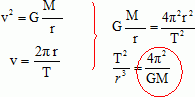Saturne et ses anneaux : concours orthoptie Nantes 2013

La planète Saturne est entourée de nombreux satellites et d'anneaux. Les anneaux sont formés de divers éléments ( cailloux, poussières et blocs de glace ) non regroupés entre eux et tournant autour de Saturne. On donne : rayon intérieur du premier anneau : 74 milliers de kilomètres. Rayon extérieur du dernier anneau : 136 milliers de kilomètres. Distance Saturne Soleil D = 1,425 109 km ; rayon de Saturne RS =60 103 km. satellite durée de révolution rayon de l'orbite ( milliers de km ) Janus 17 h 58 min 159 Mimas 22 h 37 min 185,8 Encelade 1 j 8 h 53 min 238,3 Tethis 1 j 21 h 18 min 294,9 Dione 2 j 17 h 41 min 377,9 Dans la première partie de l'exercice, on considèrera que les astres sont ponctuels et que les trajectoires sont circulaires. On rappelle la constante de gravitation G = 6,67 10-11 S.I. Partie 1. Pour étudier le mouvement des satellites de saturne, il convient de se placer dans un référentiel particulier que l'on peut appeler " saturno-centrique" par analogie à géocentrique. Comment définir le référentiel "saturno-centrique" ? Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel saturno-centrique a pour origine le centre de Saturne et des axes parallèles à ceux du référentiel héliocentrique. A l'aide d'un schéma, exprimer la force qu'exerce saturne sur un de ses satellites. Montrer que le mouvement du satellite est uniforme. En déduire la relation : v2 = GM /r. v : vitesse du satellite sur une orbite circulaire de rayon r ; M : masse de Saturne. On négligera l'action des astres autres que saturne. Le satellite est soumis à la force de gravitation exercée par Saturne. On écrit la seconde loi de Newton. La force de gravitation, seule force agissant sur le satellite,  perpendiculaire à la vitesse, ne travaille pas. L'énergie cinétique du satellite, et en conséquence la valeur de  sa vitesse, reste constante. Le mouvement du satellite est donc uniforme. La troisième loi de kepler peut s'énoncer ainsi : le carré de la période de révolution du satellite d'un astre est proportionnelle au cube du rayon de sa trajectoire circulaire. T2 = k r3. Exprimer la constante k en fonction de G et M. En utilisant les données relatives à l'un des satellites, déduire la masse de Saturne. On considère Jaunus. période T 17 h 58 min = 17*3600+58*60 = 64 680 s T2 64 6802 =4,1835 109 s2. rayon de l'orbite r 159 000 km = 159000*1000 = 1,59 108 m r3 (1,59 108)3 = 4,02 1024 m3. k 4,1835 109  / 4,02 1024 =1,04 10-15. k=4 p2/(GM) ; M = 4 p2/(Gk)  =4 *3,142/(6,67 10-11 *1,04 10-15) = 5,69 1026 kg. Partie 2. Il existe une distance R0, appelée rayon de la sphère de Roche qui marque la limite entre une zone où les satellites peuvent se former par assemblage de poussières, cailloux et une zone où cet assemblage est rendu impossible par action de l'astre. Il s'agit dans cette partie de déterminer les raisons de l'existence de cette limite qui explique en partie l'existence des anneaux de Saturne. On considère deux sphères homogènes, identiques, en contact, de masse m et de rayon r, telles que la distance entre leurs centres A et B est AB = 2 r. Le centre de gravité P de l'ensemble des deux sphères tourne à une distance r du centre S de Saturne. Les points A, B, S et P sont alignés. 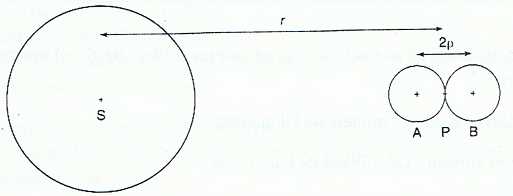Exprimer en fonction des données la valeur de la force d'interaction FAB entre les sphères. 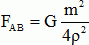Les deux sphères sont attirées par Saturne. Les forces correspondantes sont appelées F S/ A et FS / B. On montre que la valeur de la différence entre ces forces est : 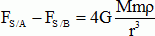 Cette différence d'attraction a tendance à séparer les deux sphères. Expliquer la raison pour laquelle les deux sphères ne sont pas attirées de la même manière par Saturne. 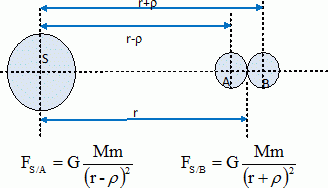Les centres des deux sphères ne se trouvent pas à la même distance du centre S de Saturne. Les forces de gravitation exercée par Saturne sur chaque sphère, sont différentes. R0, le rayon de la sphère de Roche, est tel que pour r=R0, FAB = F S/A -F S / B. L'espace où les éléments A et B peuvent se regrouper pour donner naissance à un élément plus gros est-il défini par r <R0 ou par r > R0 ? Justifier. La différence   est encore appelée "force de marées". Ces forces sont proportionnelles à l'inverse du cube d'une distance. La force d'interaction attractive entre les deux sphères est : . Cette force est proportionnelle à l'inverse du carré d'une distance. Si la distance diminue  ( r < R0 ),  les "forces de marées" l'emportent sur la force attractive FAB : les sphères se séparent. Si la distance augmente ( r >R0 ), la force attractive FAB l'emporte sur les "forces de marées" : les sphères ne se séparent pas. Les données fournies au début du texte sont-elles en accord avec l'existence de la sphère de Roche ? Justifier. Rayon intérieur du premier anneau : 74 milliers de kilomètres. Rayon extérieur du dernier anneau : 136 milliers de kilomètres. Rayon de l'orbite du satellite le plus proche de saturne, Janus : 159 milliers de kilomètres. Les données sont donc en accord avec l'existence de la sphère de Roche.

menu