|
|
Le gerris est un insecte que l'on peut observer sur les plans d'eau calmes de certaines rivières.
Très
léger cet insecte évolue sur ka surface en ramant avec ses pattes.
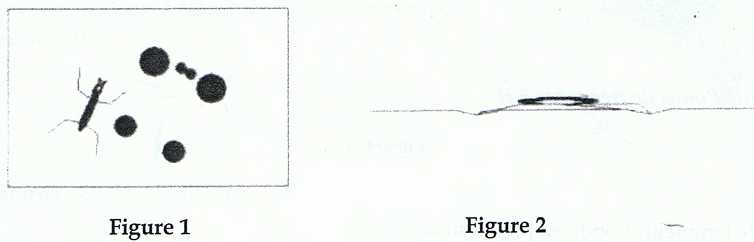
Malgré sa discrétion, sa présence est souvent trahie par des ombres
projetées sur le fond. Ces ombres ( gigure 1 ) sont la conséquence de
la déformation de la surface de l'eau au contact de l'extrémité des six
pattes de l'insecte ( figure 2).
Le déplacement de l'insecte génèrent des ondes à la surface de
l'eau qui se propagent dans toutes les diirections offertes par le
milieu. Le schéma suivant donne une vue en coue de l'onde créée par une
patte à la surface de l'eau à l'instant t.
O est le point source : point de la surface où est créée l'onde.

L'onde générée peut-elle être qualifiée de transversale ou de longitudinale ? Justifier.
L'onde est transversale : la direction de propagation est perpendiculaire à la direction de la déformation du milieu.
Un brin d'herbe flotte à la surface de l'eau.
Décrire son mouvement au passage de l'onde.
Le brin d'herbe se déplace suivant la verticale ( sans déplacement
suivant l'horizontale ). Il descend, monte puis redescent avant de se
retrouver immobile ( l'onde ne
transporte pas de matière). L'insecte retrouve sa position initiale,
dès que
l'onde est passée.
La surface de l'eau est photographiée à deux instants différents. ( échelle 1/100 ). Calculer la célérité de l'onde.
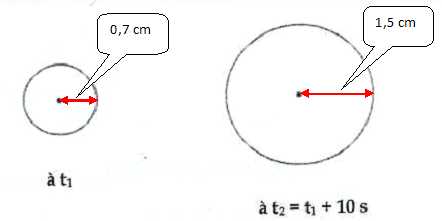
v =(1,5-0,7) *100 / 10 = 8,0 m/s.
|
.
|
Un
petit papillon tombé dans l'eau est une proie facile pour le gerris.
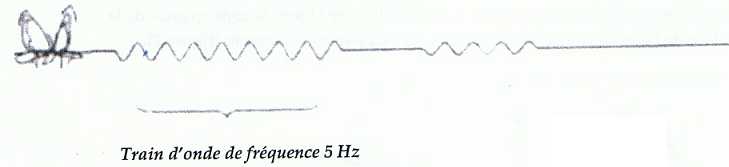
L'insecte est prisonnier de la surface crée en se débattant des trains
d'ondes sinusoïdales. La fréquence des battements des ailes du papillon
est de 5 Hz ce qui génère des ondes de même fréquence à la surface de
l'eau.
Définir la longueur d'onde.
La longueur d'onde l est la distance parcourue par le front de l'onde durant une période.
Déterminer la longueur d'onde émise par le papillon en utilisant l'aggrandissement suivant à l'échelle 2 de la surface de l'eau.
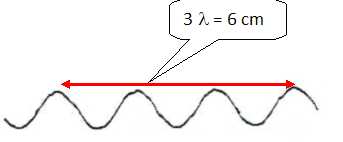
En tenant compte de l'échelle l = 1,0 cm.
Calculer la célérité de cette onde.
v = l f = 1,0 10-2*5 = 5,0 10-2 m /s = 5,0 cm/s.
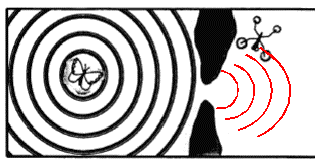
Un train d'ondes émis par le papillon arrive sur un obstacle constitué de deux galets émergeant de l'eau.
Quelle doit
être l'ordre de grandeur de la distance entre les deux galets émergeant
de l'eau pour que le gerris placé comme l'indique la figure, ait
des chances de détecter le signal de détresse généré par le papillon ?
Justifier.
L'obstacle
doit diffracter les ondes. La distance entre les deux galets doit
être de l'ordre de grandeur de la longueur d'onde, soit 1 cm.
Quel nom donne-t-on à ce phénomène propre aux ondes ?
Il s'agit de la diffraction des ondes.
Compléter la figure avec la maximum de précision en représentant l'allure de la forme de l'onde après passage de l'obstacle.
|
La
concurrence est rude sur le plan d'eau entre trois gerris. Les
extrémités de leurs pattes antérieures, situées près de leurs antennes
( zone de détection ), leur permettent de déterminer la direction et le
sens de propagation de l'onde émise par une proie.
Le papillon se débat à une distance d1=6 cm de
l'insecte n°1. L'onde générée par le papillon a mis 1 s pour parvenir à
l'insecte n°2. L'insecte n°3 détecte cette même onde avec un retard de
1,5 s sur l'insecte n°2.
- Déterminer la distance d2 entre le papillon et l'insecte
n°2.
d2 = v t = 5,0*1 = 5 cm.
Déterminer la distance d3 entre le papillon et l'insecte
n°3.
d3 = d2 + 5,0 *1,5 = 5+7,5 = 12,5 cm.
Déterminer sur la figure ci-dessous la position du papillon à l'aide
d'un compas.
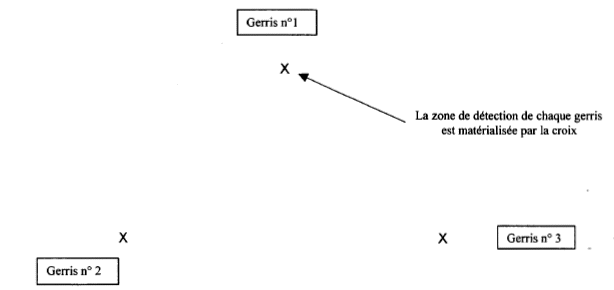
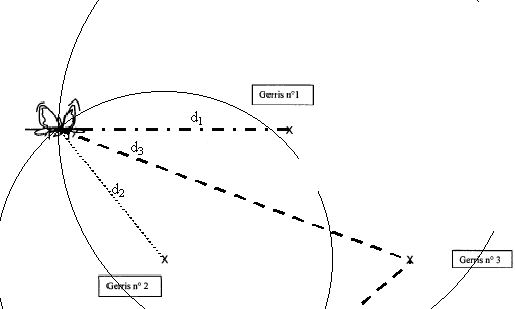
On trace un cercle de rayon 5 cm dont le centre est confondu
avec l'insecte n°2.
Il reste deux positions possibles pour le papillon.
L'insecte n°3 est plus éloigné du papillon que ne l'est
l'insecte n°2.
Une seule position est possible pour le papillon.
|
|