Mouvement sur un plan incliné, Concours orthoptie 2012.

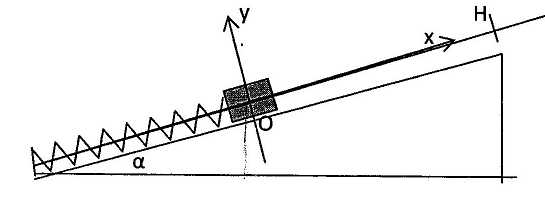
Les parties A et B sont indépendantes. On utilise un ressort d'élasticité k sur un plan incliné d'un angle a sur l'horizontale pour propulser un solide de mase m. A. Mouvement sur le plan incliné.  Le système est en équilibre quand le centre de gravité du solide est en O, origine des coordonnées x et y, le ressort subissant alors un raccourcissement Dl. Représenter sur un schéma les forces s'appliquant au solide à l'équilibre. En déduire une relation entre m, k, a, Dl et g, intensité de la pesanteur. Le solide est soumis à son poids, à l'action du plan, et à l'action du ressort. 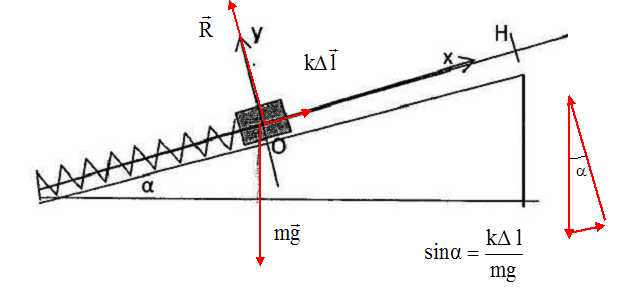On écarte le solide de sa position d'équilibre d'une distance Xm vers le bas et on le lâche sans vitesse initiale. On néglige les frottements. Par application du principe de conservation de l'énergie, établir l'expression de la vitesse V0 du solide au passage en O en fonction de m, k et Xm. L'origine des énergies potentielles est choisie en O. L'énergie mécanique initiale est sous forme potentielle : ½k(Xm+Dl)2 + mg(-Xm-Dl)sin a. ½k(Xm+Dl)2 - kDl(Xm+Dl)= k (Xm+Dl)(½Xm+½Dl-Dl) = ½k (Xm+Dl)(Xm-Dl)= ½k (Xm2-Dl2). L'énergie mécanique en O est sous forme cinétique : ½mV02. L'énergie mécanique se conserve : ½mV02 = ½k (Xm2-Dl2) = ½kXm2-½(mg sin a)2/k. V02 = k/m Xm2-m(g sin a)2/k. V0 = [  k/m Xm2-m(g sin a)2/k ]½. . Au passage en O un dispositif supprime l'action du ressort, le solide n'est plus soumis qu'à son poids et à la réaction du plan. Le plan incliné s'arrête en H. On note D la distance OH. Exprimer la vitesse VH du solide au passage en H en fonction de V0, g, D et a. L'énergie mécanique en O est sous forme cinétique : ½mV02. L'énergie mécanique en H est sous forme cinétique et potentielle de pesanteur. ½mVH2 +mgDsin a. L'énergie mécanique se conserve : ½mV02 =½mVH2 +mgDsin a. VH=[V02-2gDsin a]½. Etablir l'expression de la valeur minimum km de k en fonction de m, D, a, g et Xm pour que le solide atteigne le point H. La valeur minimale de k correspond à VH=0 : V02 =2gDsin a.  km/m Xm2-m(g sin a)2/km =2gDsin a.  km2/m Xm2-m(g sin a)2 -2gDsin a km =0.  km2 Xm2 -2mgDsin a km -(mg sin a)2=0. Discriminant de l'équation du second degré : 4(mgDsin a)2 +4(mgXm sin a)2=4(mgsin a)2 (D2+Xm2). Retenir la solution positive : km=[(mgsin a) (D+(D2+Xm2)½)] / Xm2. A.N : m = 0,030 kg ; k = 100 N m-1 ; Xm = 0,030 m ; g = 10 N kg-1 ; a = 30° ; D = 0,20 m. Calculer Dl, V0, VH et km. Dl = mg sin a / k = 0,030*10*sin 30 / 100 =1,5 10-3 m = 1,5 mm. V0 = [  k/m Xm2-m(g sin a)2/k ]½= [100/0,030*0,0302-0,030(10*0,5)2/100]½ =1,73 ~1,7 m /s. VH=[V02-2gDsin a]½= [3,0075-2*10*0,20*0,5)½=1,0 m/s.   km=[(mgsin a) (D+(D2+Xm2)½)] / Xm2 = [(0,03*10*0,5) (0,02+(0,202+0,032)½]/0,032= 67 N m-1. B. Mouvement de chute libre. 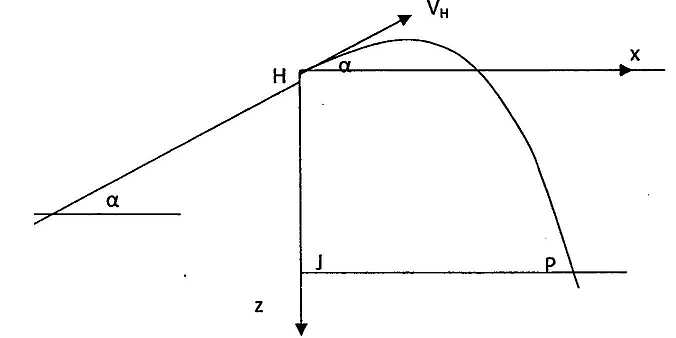En H, nouvelle origine des coordonnées, le solide n'est plus soumis qu'à son poids. En H sa vitesse fait un angle a avec l'horizontale. Le solide touche le sol en P. la droite JP est horizontale et on note h la hauteur HJ. Etablir l'équation de la trajectoire z = f(x) du mobile entre H et P. Accélération : (0 , g) ; vitesse initiale ; ( VH cos a ; -VH sin a) ; la position initiale est l'origine du repère. La vitesse est une primitive de l'accélération ; V ( VH cos a ; gt-VH sin a). La position est une primitive de la vitesse : x = VH cos a t ; z = ½gt2-VH sin a t. Eliminer le temps : z = ½g ( x / VH cos a )2 -x tan a. Exprimer l'abscisse xP du point P en fonction de a, g, VH et h. h = ½g  xP2 / (VH cos a )2 - xP tan a. (VH cos a )2 h = ½g  xP2 - xP tan a (VH cos a )2. 2(VH cos a )2 h = g  xP2 - xP 2sin a cos a VH2. g xP2 - xP sin (2a) VH2 -2(VH cos a )2 h =0. Discriminant : D= (sin (2a) VH2 )2+8g(VH cos a )2 h. Solution positive : xP =[ sin (2a) VH2 +D½] / (2g). Calculer xP à 10-2 près pour g = 10 N kg-1, a = 30°, VH = 1,0 m/s et h = 1 m. D½= (sin260 +80 cos230)½=7,794. xP =[ sin 60 +7,794] / 20= 0,43 m. Quelle valeur faudrait-il donner à Xm, à 10-3 près, pour que l'abscisse du point P prenne la valeur xP =0,57 m. Calculer vH pour xP=0,57 m : 1 =5*0,572/(VH2 cos230)-0,57 tan30. 1=2,166/VH2 -0,329 ; 1,329 =2,166/VH2 ; VH2 =2,166 / 1,329 ; VH =1,2766 m/s. Calculer V0 :  V2H=V02-2gDsin a ; 1,27662 =V02-20*0,20 sin 30 ; V0 =1,9052 m/s. Calculer Xm : V02 = k/m Xm2-m(g sin a)2/k ; 3,6297 =100/ 0,030 Xm2-0,030(10 sin 30)2/100. 3,6297 =3333,3 Xm2-0,0075 ; Xm2=1,091 10-3 ; Xm = 3,303 10-2 m = 3,303 cm.

menu