|
|
Pour mesurer le taux d'humidité relative de l'air
( % d'HR) on peut utiliser le capteur appelé
"humidistance" dont le principe utilise un condensateur de
capacité variable avec l'humidité. On place ce
condensateur dans le circuit ci-dessous dans lequel la
bobine a une résistance négligeable.
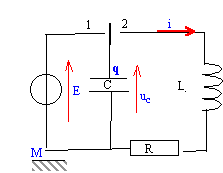
L'interrupteur est d'abord placé en position 1
pour charger le condensateur, puis basculer en position 2
pour le décharger. Un système
informatisé d'acquisition de données permet de
relever la tension aux bornes du condensateur au cours de la
décharge.
- Suivant la valeur de la résistance R non
nulle, l'évolution du système (RLC) se fait
suivant deux régimes différents. Tracer
l'allure de la tension aux bornes du condensateur en
fonction du temps pour ces deux régimes que l'on
nommera.
- On suppose maintenant que R=0 . Reproduire la partie
du circuit correspondant à la décharge .
Etablir l'équation différentielle
régissant l'évolution de la charge q du
condensateur.
- Vérifier que l'expression q= QM cos
(2pt/T0+F0)
est solution de l'équation différentielle
si la période propre T0 a pour
expression : T0 = 2p
(LC)½.
- Le condensateur du capteur d'humidité est
introduit dans le circuit précédent. La
période mesurée T vaut 31,4 ms
dans les conditions atmosphériques de
l'expérience. Sachant que l'inductance de la
bobine L=200 mH, calculer la capacité du
condensateur.
- On lit sur la notice de l'appareil :
gamme de mesures 10 à 100 % d'HR ;
sensibilité 0,4 pF par % d'HR ; capacité
à 25°C et à 43% d'HR : 122 pF ;
température d'utilisation : 0 à 85
°C.
-
- L'expression de la capacité C du condensateur
est une fonction affine croissante du taux d'HR
noté h, exprimé en % d'HR. On peut donc
écrire C=a h + b. Déterminer les valeurs
des constantes positives a et b.
- Dans le cadre des données ci-dessus
déterminer le %d'HR de l'atmosphère.
|
.
|
Corrigé.
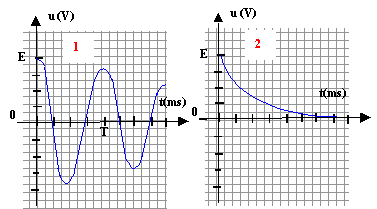
(1) régime
pseudo-périodique: R faible
(2) régime
apériodique : R élevée.
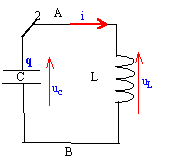
uc=uL soit
q/C = Ldi/dt avec i = -dq/dt ( décharge) et di/dt =
-d²q/dt² = -Lq"
q/C = -Lq" soit
q"+
w0²
q=0 avec
w0²
=(LC)-1 et 2p/T0=
w0.
q= QM cos (w0+F0)
; dérivée première par rapport au temps
q' = QM w0(
-sin(w0+F0))
q" = -QM w²0cos
(w0+F0)
= - w²0q
repport dans l'équation différentielle de
la charge : - w²0q
+ w²0q=
0 , vérifiée quel que soit t.
capacité :
T =2p
(LC)½ soit T²=
4p2
(LC) d'où : C= T²/
(4p2L)=
(31,4 10-6)2/( 4*3,14²*0,2) =
1,25 10-10 F= 125
pF.
a= 0,4 pF %HR-1.
122 = 0,4 * 43+b d'où b =
104,8 pF
C= 0,4 h
+104,8.
h=(C-104,8 )/ 0,4 = (125-104,8) /
0,4 = 50,5 %
d'HR.
|
Etude énergétique.
On souhaite étudier l'énergie
totale E de l'oscillateur électrique. Cette
énergie est la somme de l'énergie
électrique E1 = ½
CuC2 emmagasinée dans le
condensateur et de l'énergie magnétique
E2 = ½ Li 2 emmagasinée
dans la bobine. Le logiciel utilisé peut calculer,
à partir des mesures, les valeurs de ces trois
énergies et fournir les courbes donnant leur
variation en fonction du temps.
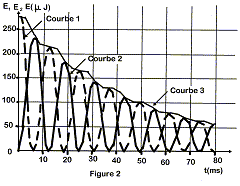
- L'origine des dates étant la même pour
toutes les courbes des figures 1 et 2, identifier les
trois courbes données figure 2 en ne justifiant
que l'identification de la courbe donnant les variations
de l'énergie magnétique.
-Interpréter brièvement la
décroissance de l'énergie totale de
l'oscillateur électrique.
- Evaluer l'énergie dissipée pendant les 50 premières millisecondes.
Courbe 1 : E1
= ½ CuC2
à t=0, le condensateur stocke toute l'énergie
du dipole LrC.
courbe 2 : E2
= ½ Li 2
à t =0,25 T, la bobine stocke toute
l'énergie du dipole.
courbe 3 : E = E1+E2.
Lors des échanges d'énergie entre
condensateur et bobine, une partie de l'énergie est
perdue par effet joule dans les parties résistives :
E décroît au cours du temps.
Ainsi durant les 50 premières millisecondes, l'énergie totale diminue de 300 à 100 µJ.
|
|



