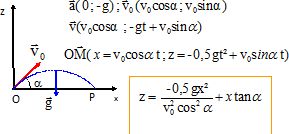Lancement d'une sonde vers Jupiter, mouvement parabolique, ; concours orthoptie Montpellier 2011.

On a représenté les orbites circulaires de la terre ( rayon RT) et de Jupiter ( rayon RJ ) autour du soleil. A l'instant choisi pour le lancement de la sonde la terre est en A et Jupiter est en B. Le rendez-vous doit se produire en C. L'orbite que va décrire la sonde est une ellipse tangente en A et en C aux trajectoires de la Terre et de Jupiter, appelée orbite de transfert. On rappelle qu'une éllipse est caractérisée par son demi-grand axe a. Dans le cas particulier d'une orbite circulaire, a correspond au rayon. G = 6,67 10-11 SI. RT = 1,5 1011 m ; RJ = 7,8 1011 m ; Tterre = 365,25 j. Exprimer le demi-grand axe a de l'orbite de transfert en fonction de RT et RJ et calculer sa valeur. a = ½( RT +RJ ) = 0,5 (1,5+7,8) 1011 =4,65 1011 ~4,7 1011 m. La 3ème loi de Kepler dit que le rapport T2/a3 est constant, T étant la période du mouvement et a le demi-grand axe de la trajectoire. En déduire la durée du transfert de A en C en jours. T2/a3 = T2terre / RT3 ; T2 = T2terre a3/ RT3 ; T = Tterre (a / RT)1,5. T = 365,25 (4,65 / 1,5)1,5 = 1,9936 103 ~2,0 103 j. Calculer la valeur de la période de Jupiter en jours. T2J / R3J=T2terre / RT3 ; T2J = T2terre RJ3/ RT3 ; TJ = Tterre (RJ / RT)1,5. TJ = 365,25 (7,8 / 1,5)1,5 = 4,331 103 ~4,3 103 j. En déduire la valeur en degré de l'angle ASB qui donne la position de Jupiter au moment du lancement. 2 p RJ = vJ TJ et arc (BC) = vJ T ; arc (BC) =2 p RJ T / TJ ; arc (BC) =angle ( ASB) RJ. angle ( ASB) = 2 p T / TJ  = 6,28 *1,9936 / 4,331 =2,892 rad ou ~166°. Si le lancement est annulé, combien de temps faut-il attendre pour que la Terre et Jupiter se retrouvent dans la même position. Rechercher le plus petit multiple commun  de Tterre et TJ :  PPCM ( 365 et 4300 ) = 365*4300 / PGCD(365 et 4300) = 365*4300/5 = 3,1 105 j. Donner l'expression de la force attractive exercée par le soleil, de masse MS sur un solide de masse m situé à la distance r. F = G MS m / r2. Dans le cas d'un mouvement circulaire uniforme, exprimer cette force en fonction de m, r et T. La troisième loi de Kepler s'écrit : T2/ r3 = 4 p2/(GMS) ; GMS = 4 p2r3/ T2. Repport dans l'expression de la force : F = 4 p2r m / T2. Exprimer MS en fonction des autres données. MS =4 p2r3/ ( GT2). Calculer MS  en appliquant cette expression au cas de la terre. MS =4*3,142 *(1,5 1011)3 / (6,67 10-11 * (365,25*24*3600)2) =2,0 1030 kg. Mouvement parabolique. 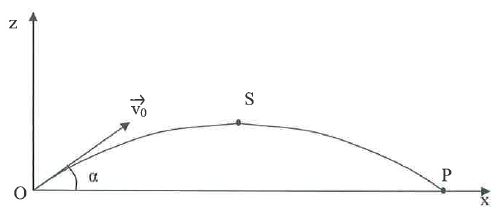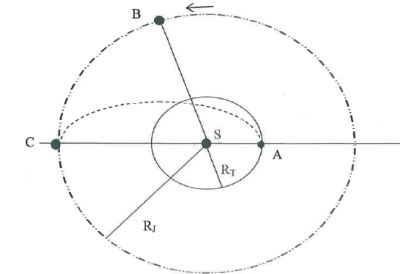Un solide ponctuel de masse m est lancé du point O à la date t=0 avec une vitesse initiale v0 faisant un angle a avec l'horizontale. On néglige les frottements, le solide n'est soumis qu'à son poids. g = 9,81 m s-2. Etablir les lois horaires x(t) et z(t). 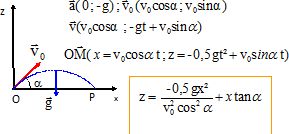Exprimer OP en fonction de v0, a et g. Calculer OP si v0 = 30 m/s et a = 20°. z =0 ; simplifier chaque terme de z(t) par xP / cos a : 0,5 g xp = v02cos a sin a ; xp = v02sin (2a) / g = 302 sin 40 / 9,81 =58,97 ~59,0 m. Quelle est la valeur maximum de la portée ? Pour sin (2a)  =1, soit a = 45°, la portée est maximale : OP = v02 / g =900 / 9,81 = 91,7 m. Quelle(s) valeur(s) faut-il donner à a pour que la trajectoire passe par le point M de coordonnées x = 30 m et z = 8 m ? v0 = 30 m/s. 30 = 30 cos a t ; t = 1 / cos a.  8 = -4,9 t2 +30 sin a t ; 8 = -4,9/ cos2 a + 30 tan a. Or 1/ cos2 a = 1 + tan2 a. 8 = -4,9 -4,9 tan2 a + 30 tan a. On pose X =tan a : -4,9 X2 + 30 X -12,9 = 0. Résoudre : D = 302-4*12,9*4,9 = 647 ; D½ =25,4. X1 = (-30+25,4) / (-4,9*2)=0,465 ; X2 = (-30-25,4) / (-4,9*2)=5,64 ; a1 = 24,9 ° ; a2 = 79,9 °. Quelle est la valeur de la vitesse  au passage en M ? t =1/ cos a = 1/ cos 24,9 = 1,1 s ; vx = 30 cos 24,9 = 27,2 m/s ; vz = -9,81 *1,1 + 30 sin 24,9 = 1,84 m/s. v = (27,22 + 1,842)½=27,3 m/s. L'autre valeur de a donne le même résultat. Etablir la relation entre x, z, v0 et g qui doit être satisfaite pour qu'un point de coordonnées (x, z) puisse être atteint par le projectile. En déduire l'équation de la courbe qui limite la zone dans laquelle un point peut-être atteint.   z =  -½g x2/ (v02cos2 a )+ x tan a. Or 1/ cos2 a = 1 + tan2 a. z =  -½g x2/ v02-½g x2/ v02tan2 a + x tan a. On pose X =tan a : z +½g x2/ v02 +½g x2/ v02 X2 - xX=0. Pour x et z donnés, le discriminant de cette équation du second degré doit être positif ou nul : D = x2- 2g x2/ v02(z +½g x2/ v02)>=0. Dans le cas limite le point M appartient à la parabole de sureté : x2- 2g x2/ v02(z +½g x2/ v02)=0. 1-2g / v02(z +½g x2/ v02)=0 ; v02 / (2g) = z +½g x2/ v02. z = v02 / (2g)-½g x2/ v02.

menu