QCM de physique , d'après concours kiné Alençon 2013.

Fente d'Young. Durant tout l'exercice, la largeur de la fente est a = 1 mm, la distance à l'écran est D = 2 m.  On donne l'interfrange i = l D/a. Expérience 1 : On utilise une radiation de longueur d'onde l1 et on observe que la distance entre le centre de la première frange brillante ( frange centrale ) et la 10è frange brillante est de 9,9 mm. Quelle est la valeur de l1 ? Entre la frange centrale brillante et la 10è frange brillante il y a 9 interfranges : i = 9,9 / 9 = 1,1 mm = 1,1 10-3 m. l1 = i a / D = 1,1 10-3*10-3 / 2 = 5,5 10-7 m = 5,5 10-4 mm. Expérience 2 : On considère maintenant une autre radiation de longueur d'onde l2 ; on observe que la 6ème frange sombre ( avec l2) coincide avec la 8è fraange brillante de l1. 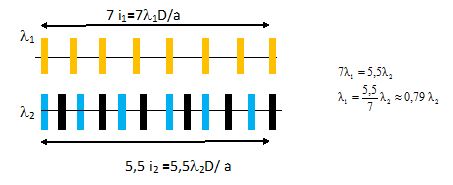A)  i est plus grand avec l2 qu'avec l1. Vrai. B) l2 est plus grand que l1. Vrai. l2 = 5,5 10-7 /0,79 ~7,0 10-7 m. Propagation du son. On frappe à l'extrémité d'un tube d'acier de longueur L =800 m ; on perçoit deux sons à l'autre bout du tube. Le décalage entre les deux sons est Dt = 2,19 s. On donne la célérité du son dans l'air à 20 °C. V = 340 m/s. A) Le son se propage moins vite dans l'acier que dans l'air. Faux. B) Vacier ~5000 m/s. Vrai. Le son se déplaçant dans l'air est perçu à la date t1 =L / V= 800 / 340 =2,35 s. Le son se déplaçant dans l'acier est perçu à la date t2 = t1-Dt = 2,35-2,19 = 0,16 s. Vacier = L / (t1-Dt )= 800 / 0,16 ~4,9 103 m/s. D) Vacier = V2 / (Dt L). Faux. Cette expression n'est pas homogène. [V2 / (Dt L)] s'exprime en m2 s-2 / (m s) soit en m s-3  ; [Vacier] s'exprime en m s-1. Mécanique. Un skieur de masse m = 60 kg descend le long d'une piste inclinée d'un angle a = 30 ° par rapport à l'horizontale. Il est soumis entre autres à la réaction Rn du plan, perpendiculaire à la piste et à la force de frottement f. Quelles sont les valeurs de Rn et f ? Dans l'hypothèse ou la valeur de la vitesse du skieur est constante ( mouvement uniforme ). 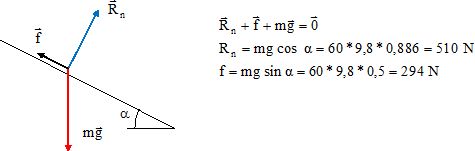A) L'énergie mécanique diminue constamment au cours du temps. Vrai. L'énergie mécanique diminue du travail des frottements. B) L'énergie mécanique augmente constamment au cours du temps. Faux. Le skieur est maintenant sur un tronçon verglacé d =30 m de long et les frottements sont négligeables. Sa vitesse d'arrivée au bout du tronçon est 80 km/h. Quelle était sa vitesse initiale au début du tronçon ? Seul le poids travaille, l'action du plan étant perpendiculaire à la piste. Travail moteur du poids en descente : mg d sin a = 60*9,8*30*0,5=8,8 103 J. vf = 80 / 3,6 =22,2 m/s. Ecrire le théorème de l'énergie cinétique entre le début et la fin du tronçon : ½mv2f -½mv2i = mg d sin a ; v2i =v2f -2g d sin a  =22,22 -2*9,8*30*0,5 =14,1 m/s ( 14,1 *3,6 ~51 km/h ). . Onde sonore. A) L'intensité sonore est donnée par la relation  10 log ( I / I0). Vrai. Le seuil de la douleur est atteint à L=120 dB ; cela correspond à une intensité sonore de : (1,2 10-10 W m-2 ; 1 W m-2 ; 1,2 W m-2 ; 1,2 10-11 Wm-2. I = I0 100,1 L = 10-12 * 1012 = 1 W m-2. Un individu situé à d1=8 m de la source atteint le seuil de la douleur. Sachant que l'intensité sonore diminue proportionnellement au carré de l'inverse de la distance, de combien de mètre l'individu doi-il reculer afin de percevoir une intensité de 60 dB ? I1  d12 = I2  d22 = constante. I1 = 10-12 * 1012 = 1 W m-2 ; I2 =10-12 * 106 = 10-6 W m-2. d22 =I1  d12 / I2 =82/10-6 =82 *106 ; d2 =8 103 m. d2-d1 = 8000-8 = 7992 m. Son joué au violon. On donne le spectre en fréquence d'un son joué au violon. 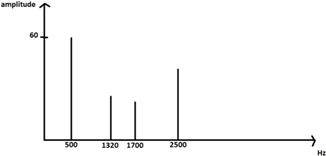A) Le même son joué par un autre instrument donnera le même spectre. Faux. Le spectre ne possèdera pas les mêmes harmoniques. B) Le son est audible entre 1320 Hz et 1700 Hz. Faux. L'oreille humaine perçoit les sons dont les fréquences sont comprises entre 20 Hz et 20 000 Hz. C) La hauteur de ce son est 60 mV. Faux. La hauteur du son est la fréquence du fondamental. Diagramme énergétique de l'hydrogène.  On donne E = -13,6 / n2 ( en eV). A) Le niveau fondamental est de 0 eV. Faux. Le niveau fondamental correspond à n = 1 soit -13,6 eV, c'est le niveau de plus basse énergie. B) Les trois premiers niveaux excités sont -3,40 , -1,56 , -0,80 eV. Faux. E2 = -13,6 / 22 = -3,40 eV ; E3 = -13,6 / 32 = -1,51 eV ; E4 = -13,6 / 42 = -0,85 eV. C) Le niveau -2,5 eV n'existe pas. Vrai. En passant des deux premiers niveaux excités au fondamental, deux raditions sont émises. Quelles sont les longueurs d'onde de ces radiations ? E2-E1 = -3,40 + 13,6 = 10,2 eV ou 10,2 *1,6 10-19 = 1,63 10-18 J. l = hc = (E2-E1) =6,62 10-34 * 3,00 108 / (1,63 10-18) =1,21 10-7 m = 121 nm. E3-E1 = -1,51 + 13,6 = 12,09 eV ou 12,09 *1,6 10-19 = 1,93 10-18 J. l = hc = (E3-E1) =6,62 10-34 * 3,00 108 / (1,93 10-18) =1,03 10-7 m = 103 nm. Mécanique. 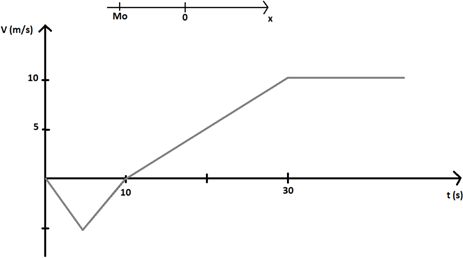A t=0 : A) le solide est immobile. Vrai. La vitesse initiale est nulle. B) Le mobile est déja en mouvement. Faux. C) Le mobile se déplace vers la droite. Faux. A t=0+, le vecteur vitesse est en sens contraire de l'axe Ox ( v est négative). D) Le mobile se déplace vers la gauche. Vrai. A t = 20 s : A) Le mouvement est uniforme. Faux. La valeur de la vitesse n'est pas constante. B) Le mouvement est uniformément varié. Faux. L'accélération est constante de valeur égale à la pente du segment de droite compris entre t = 10 s et t = 30 s. a = 10 / 20 = 0,5 m s-2. C) L'accélération vaut 0,75 m s-2. Faux. Quelle est la distance parcourue en 40 s ? 0< t < 5 s :  mouvement uniformément accéléré, vitesse initiale nulle, abscisse initiale  nulle : d = ½at2 avec a =Dv / Dt = (-5-0) / 5 = -1 m s-2 ; le signe moins traduit un déplacement en sens contraire de l'axe. Distance parcourue d1 = 0,5*1*52 = 12,5 m ; vitesse atteinte v1 = 5 m/s. 5 < t < 10 s : mouvement uniformément décéléré, vitesse initiale -5 m/s, abscisse initiale x1 =-2,5 m  : x = ½at2 avec a =Dv / Dt =0-(- 5) / 5 = 1 m s-2 . Distance parcourue : d2 = -½ a (t-5)2 +v1(t-5) = 0,5*52 +5*5 = 12,5 m. Arrêt à t = 10 s et changement de sens du déplacement. 10 < t < 20 s : mouvement uniformément accéléré dans le sens de l'axe avec une vitesse initiale nulle et a = 0,5 m/s. Distance parcourue : d3 = ½a(t-10)2 = 0,5*0,5*202 =100 m. 30 < t < 40 s: mouvement uniforme de vitesse 10 m/s. Distance parcourue : 10*10 = 100 m. Distance totale parcourue : 12,5+12,5+100+100 = 225 m. Autre méthode : La distance parcourue est l'aire comprise entre la courbe et l'axe des x. 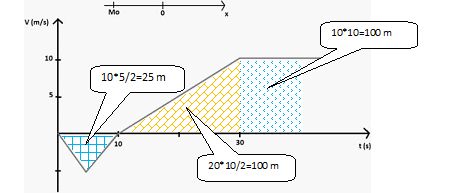Durant 40 s : A) le mobile a changé 3 fois de sens. Faux. B) Le mobile a changé une fois de sens. Vrai. C) Le mobile se déplace dans le même sens que Ox. Faux. D) Le mobile se déplace en sens inverse de Ox. Faux. Entre t = 0 et t=10 s, déplacement en sens contraire de l'axe ; à t = 10 s : arrêt ; à t > 10 s, déplacement dans le sens de l'axe. Synthèse additive. 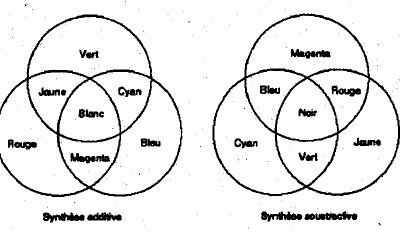Un objet éclairé en lumière blanche paraît magenta. Pour qu'il apparaisse bleu, comment faut-il l'éclairer ? L'objet absorbe le vert, couleur complémentaire du magenta, mélange du rouge et du bleu. Eclairé en lumière bleue, il paraît bleu. Pour qu'il apparaisse rouge, comment faut-il l'éclairer ? Eclairé en lumière rouge, il paraît rouge. Pour qu'il apparaisse noir, comment faut-il l'éclairer ? Eclairé en lumière verte, il paraît noir.

menu