|
|
Déviation
d'un
électron.
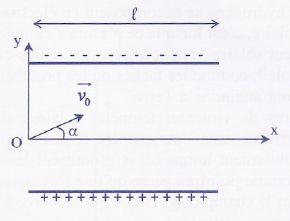
Un électron, de masse m et de charge (-e), pénètre au point 0, avec une
vitesse V0 faisant un angle a = 30° avec le
plan horizontal,
dans un champ électrostatique uniforme E créé par deux armatures
chargées. La vitesse d'entrée de l'électron a pour valeur V0=
2,00 x 107m / s.
Dans l'exercice, on négligera le poids devant la force électrique
exercée sur l'électron.
Données
: l=
10,0 cm ; m = 9,11 10-31
kg ; E = 5,70 104 V m-1 ;
e = 1,60 10-19
C ;
sin(30) = 0,5 ; cos 30 ~0,87 ;tan 30 ~0,57 ; 5/3 ~1,67 ; 1,60 *5,70 /
9,11 = 1,00.
a) Le champ électrique est perpendiculaire aux
armatures et de sens vers le bas. Faux
Le champ
électrique est
perpendiculaire aux armatures et dirigé vers le haut.
b) Les équations horaires du mouvement de l'électron sont : x(t) = v0
cos a t ;
y(t) = Ee / (2m) t2
+ v0
sin a t.
Faux.
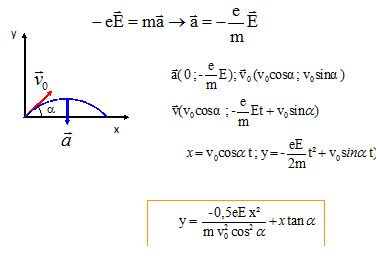
c)
L'équation de la trajectoire
est y(x) =- Ee / (2m [x / (v0cos a)]2
+x tan a.
Vrai
d) L'électron sort des plaques à l'ordonnée Ysortie~
-0,11 m. Vrai.
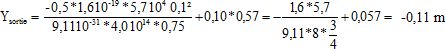
|
.
|
Particule
chargée dans un champ électrique.
En présence d'un champ électrique uniforme E, la trajectoire d'une
particule ponctuelle chargée ne peut jamais être :
A) un arc de cercle. Vrai.
B)
une parabole.
Faux.
La
trajectoire est un arc
de parabole si le champ et le vecteur vitesse initial n'ont pas la même
direction.
C) Une droite. Faux.
La
trajectoire
est une droite si le champ et le vecteur vitesse initial ont la même
direction.
D) Une particule ß+ ne peut pas être déviée en
pénétrant
dans un champ électrique E. Faux
Toute
particule chargée
peut être déviée par un champ électrique.
E) Un neutron ne peut pas être déviée
en pénétrant dans un champ électrique E. Vrai.
Un neutron
ne possède pas
de charge électrique.
Canon à
électron.
Les électrons pénètrent en A (potentiel VA) dans un
champ électrostatique uniforme E qui permet de les accélérer et
ressortent au point B (potentiel VB).On suppose que la
vitesse d'entrée au point A est quasi nulle. L'électron n'est soumis
qu'à la force électrostatique F conservative à l'intérieur du canon. On
note d la longueur de la zone d'interaction. Lorsque l'électron arrive
au point X (potentiel Vx), sa vitesse est vx.
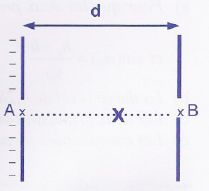
d
Données :
Charge élémentaire e = 1,60 x 10-19C; Masse de l'électron m
= 9,11 x 10-31kg ;
VA = - 4,55 x 103 V ; VB = 0 V ;
d = 10,0 cm ; 4,55 x l,60 / 9,11 =0,800.
L'énergie potentielle électrique d'une charge q en un point A est Ep(A)
= qVA.
a) Le champ électrostatique a pour valeur E = 455 V m-l. Faux
E = |VA-VB|
/ d = 4,55 103 / 0,100 =4,55 104
V m-1.
b) Le travail de la force électrostatique F, lorsque l'électron se
déplace de X à B, est W = e(Vx-VB). Faux.
W = -e(VX-VB).
c) A une constante près, l'énergie mécanique de l'électron au point X
est Em(X) =½mvx2 -eVx. Vrai.
d) La vitesse au point B est vB=2,00 x 107 m.s-l.
Faux.
Conservation de l'énergie
mécanique : ½mvB2
-eVB = ½mvA2 -eVA.
vB2
=-2e/mVA
; vB = (2e/mVA)½ =(2*1,6 10-19
* 4,55 103 / 9,11 10-31)½
=(2*0,8 1015)½ =4,0 107
m/s.
|
|
Indiquer le schéma correct donnant la direction et le sens de la force
électrique qui s'exerce sur un électron, en mouvement entre deux
plaques chargées A et B, si la différence de potentiel entre celles-ci
est UAB >0.
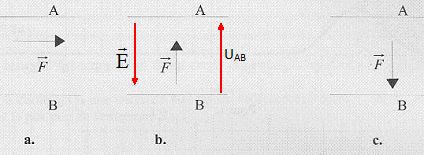
Un électron
porte une
charge négative. Schéma b.
La
force électrique
qui s'exerce sur cet électron placé dans ce champ électrique s'écrit :
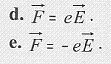 e) est vrai. e) est vrai.
Un
électron de masse m et de charge -e, est émis sans vitesse initiale
depuis le point O. Entre les plaques A et B règne un champ
électrostatique E uniforme. On notera UBA = U.
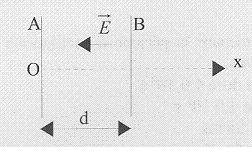
A) U <0. Faux.
Le champ
électrique E
pointe vers le plus petit potentiel : UBA
>0, UAB <0.
B) L'expression de la coordonnée du vecteur vitesse de
l'électron
en mouvement est donnée par : v = ed t / mU. Faux.
E = U/d ;
Norme de la
force à laquelle est soumise l'électron : F = e E =e U/d. Cette force
est horizontale à droite.
Accélération
subie par
l'électron a = e U/(md). Vitesse : primitive de
l'accélération v = e U/(md) t + vinitiale.
C) Le mouvement de l'électron est rectiligne uniformément accéléré.
Vrai.
D)
Lorsque l'électron atteint la plaque B la coordonnée du vecteur vitesse
est v = (eU/m)½. Faux.
Théorème de
l'énergie
cinétique entre A et B ( le poids est négligeable davant la force
électrique ) :½mv2 -0 = eU ;
v = (2eU/m)½.
E) La variation d'énergie potentielle électrostatique de l'électron,
pour le déplacement de O en B s'écrit DEp
= eU. Faux.
O est
l'origine de
l'énergie potentielle ; écrire la conservation de l'énergie mécanique
de l'électron entre O et B.
0 = ½mv2 + EpB.
EpB
= - ½mv2
= -eU.
Variation d'énergie potentielle de O à B : EpB - EpA =EpB -0 =
-eU.
|
|