|
|
On
considère une moto M et une voiture V sur une route plane rectiligne :
à t = 0, V est à la distance D ( D positive ) devant M, et ralentit
avec une accélération constante de norme "a" ; sa vitesse initiale est
notée v. A la même date initiale, M démarre avec une accélération
constante de valeur " a'".
Question
1.
On note T la date à laquelle M dépasse V. On peut affirmer que :
A) 2D = (a+a')T2-vT.
Vrai.
La voiture ralentit : xV
= -½a t2 + vt + D ; la moto accélère : xM
= ½a't2.
A la date T : xV =xM : -½a T2 + vT + D = ½a'T2
soit (a' +a) T2 -2vT - 2D =0 (1).
B) T =(v+2aD)½ / (a+a'). Faux.
Discriminant de (1) : D = 4v2+8D(a+a') ; T
=(2v +(4v2+8D(a+a'))½ )
/ (2(a+a')).
T =(v +(v2+2D(a+a'))½ )
/ (a+a').
C) T =(v-2aD)½ / (a+a'). Faux.
D) T =(v2+a'D)½ / (2a). Faux.
E) T =(v +(v2+2D(a+a'))½ ) / (a+a'). Vrai.
F) Aucune proposition ne convient. Faux.
Question
2.
On note T ' la date à
laquelle les vitesses de M et V sont égales. On peut dire que :
A) T ' = a/v. Faux.
Voiture vV =
-at+v ; moto : vM = a't ;
à la date T ' : vV =vM
= v'. -aT ' + v = aT ' = v' ; T ' = v / (a+a') ou T ' = v'
/ a' ou T ' = (v'-v) / a.
B) T ' = v / a'. Faux.
C) T ' =(aD)½
/a' . Faux.
D) T ' = v / (a+a'). Vrai.
E) T ' = v /(2a). Faux.
F) Aucune propositionne convient. Faux.
Question
3.
A la date T ' la distance parcourue par M est :
A)
d = v2/(2a2). Faux.
d = ½a' T ' 2
= ½ a' v2 / (a+a')2.
Ou bien : d = -½a v2
/ (a+a')2 +
v2 / (a+a') + D.
B) d = v2/(a'2
+ a2). Faux.
C)
d = v2 / (2(a'2 + a2)). Faux.
D) d = v2/(2a2)+D.
Faux.
E) d = D-v2/(2a2). Faux.
F) Aucune proposition ne convient. Vrai.
|
.
|
Question 4.
On donne a = 1,0 m s-2 ; a' = 0,50 m s-2 ; v =
1,0 103 cm /s ; D = 100 m. On peut dire que :
A) T = 10 s. v = 10 m/s.
T =(v +(v2+2D(a+a'))½ )
/ (a+a') = (10 +(102+200(1+0,5))½ )
/ 1,5 ~ 20 s.
B) T = 20 s. Vrai.
C) T = 30 s. Faux.
D) T ' = 4,0 s. Faux.
T ' = v /
(a+a') = 10 / 1,5 =6,7 s.
E) T ' = 5,0 s. Faux.
F) Aucune proposition ne convient. Faux.
Question
5.
On note v' la vitesse atteinte par M à la date T '. On peut dire que :
A) v' = 3,3 m/s. Vrai.
v' = a' T ' = 0,5 *6,7
~3,3 m/s.
B) v' = 6,5 s. Faux.
C) v' = 9,5 s.
Faux.
D) d ~ 9 m. Faux.
d = ½a' T ' 2
= 0,25 *6,72 ~11 m.
E) d~11 m. Vrai.
F) Aucune proposition ne convient. Faux.
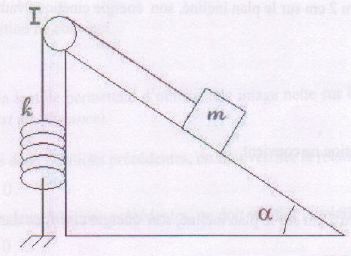
La raideur du ressort est notée k. Le ressort est relié à un bloc de
masse m par un fil ( par l'intermédiaire d'une poulie en I qui ne
jouera aucun rôle par la suite ). le dispositif est initialement au
repos, le ressort est détendu. On néglige les frottements. On ne
s'interesse qu'à la première descente du bloc ( on n'étudie pas les
oscillations et montées suivantes ).
Question
6.
La distance maximale parcourue par le bloc après avoir lâché le système
s'écrit :
A) d = mg cos a / k. Faux.
Conservation de l'énergie
mécanique : l'origine de l'énergie potentielle est la position initiale.
0 = ½k x2 -mgdsin a
avec x =d ; ½k d = mgsin a ; d = 2 mg sin a / k.
B) d = mg sin a
/ k. Faux.
C) d = 3mg cos a
/ k. Faux.
D) d = 3mg sin a
/ k. Faux.
E) d = 2mg sin a / k. Vrai.
F) Aucune proposition ne convient. Faux.
Question 7.
La distance maximale parcourue par le bloc après avoir lâché le système
vaut :
m = 100 g ; g = 10 SI ; a
= 30° ; k = 20 N/m.
A) d = 5 cm. Vrai.
m = 0,10 kg ; d = 2*0,10
*10 *0,5 / 20 =0,05 m = 5 ,0 cm .
B) d = 4 cm. Faux. C) d = 3
cm. Faux ; D) d = 2 cm. Faux ; E) d = 1 cm. Faux.
F) Aucune proposition ne convient. Faux.
|
|
Question 8.
Le graphe qui représente l'énergie cinétique du bloc en fonction
de la distance parcourue est :
A) Une droite. Faux.
Conservation de l'énergie
mécanique à une date t : 0 = ½mv2 +½kx2 -mg
x sin a.
½mv2 = -½kx2 +mg x sin a.
B) Une droite qui
passe par l'origine. Faux.
C) Un cercle. Faux.
D) Une parabole.Vrai.
E) Une sinusoïde. Faux.
F) Aucune proposition ne convient. Faux.
Question
9.
Quand le bloc a parcouru 2 cm sur la plan incliné, son énergie
cinétique vaut :
A) 7 mJ. Faux.
½mv2 = -½*20 *0,022 +0,10 * 10 *0,02
*0,5 =-0,004 +0,01 =0,066 J = 6 mJ.
B) 6 mJ. Vrai.
C) 5 mJ. Faux. D) 4 mJ. Faux. E) 3 mJ. Faux. F) Aucune proposition ne
convient.
Question 10.
Quand le bloc a
parcouru 2 cm sur la plan incliné, son énergie cinétique dans le
système international peut s'écrire :
A)
0,01 mg sin a-0,2k. Faux.
-½k 0,022 +mg 0,02 sin a = -2 10-4
k+0,02 mg sin a.
B) 0,05 mg sin a-0,2k. Faux.
C) 0,1 mg sin a-0,2k. Faux.
D) 0,1 mg sin a-0,2k.
Faux.
E) 0,1 mg sin a-0,1k. Faux.
F) Aucune
proposition ne convient. Vrai.
|
|