|
|
Pile
en court-circuit.
On a relevé expérimentalement la tension UPN aux
bornes d'une pile électrochimique lorsqu'elle débite un courant
d'intensité I. On a regroupé les résultats des mesures dans le tableau
suivant :
| UPN(
V) |
4,49 |
4,39 |
4,29 |
4,19 |
4,09 |
3,99 |
| I(mA) |
27 |
52 |
77 |
102 |
127 |
152 |
Un dipole est en court-circuit quand ses deux bornes sont reliées
directement par un fil de connexion. La tension aux bornes d'un fil de
connexion est nulle.
Calculer
la valeur de l'intensité ICC ( en A)
du courant électrique que la pile délivre lorsqu'elle est en
court-circuit. (1,15 ; 1,35 ; 1,48 ; 1,75 ; 2,76 ; aucune
réponse exacte ).
Tension aux bornes d'une pile : UPN
= E-r I.
4,49 = E -0,027 r et 3,99 = E -0,152 r.
4,49-3,99 =(0,152-0,027) r ; r = 0,50 / 0,125 = 4,0 ohms.
Par suite E = 3,99+0,152*4 ~4,6 V.
ICC = E / r = 4,6 / 4 = 1,15 A.
Génératrice
de courant continu.
Une génératrice de courant continu
convertit de l'énergie mécanique en énergie électrique. Une génératrice
alimente en courant continu une installation électrique pendant une
durée de 360 minutes.
La tension aux bornes de la génératrice est alors UPN
=114 V et elle délivre un courant électrique d'intensité I = 12,2 A.
Pendant cette durée, la génératrice a reçu une énergie mécanique Wm
= 35,8 MJ.
Calculer
la valeur de la résistance interne ( en ohm ) de la génératrice.
( 1,2 ; 1,4 ; 1,6 ; 1,8 ; 2,0 ; aucune réponse exacte ).
Puissance électrique fournie par la génératrice : UPN
I = 114 * 12,2 =1390,8 W.
Energie électrique fournie au circuit : E = 1390,8 *360*60
=3,00 107 J = 30 MJ.
Pertes par effet Joule : Wm-E
= 35,8-30 = 5,759 MJ.
Puisance Joule correspondante : PJ=5,759 106
/(360*60) =266,61 W
r = PJ / I2
=266,61 / 12,22 =1,8
ohms.
|
.
|
Réacteur
nucléaire.
Un réacteur nucléaire fonctione à l'aide d'uranium enrichi en isotope
235. Les noyaux d'uranium 235 subissent différentes fissions, parmi
lesquelles l'une des plus fréquentes est la suivante :
23592U + 10n
---> 13852Te + 9540Zr
+ 310n.
Masse du neutron : mn = 1,00866 u ; m(23592U) = 234,9933 u ; m(9540Zr) =94,8860 u ; m(13852Te) =137,9007 u.
1 u = 1,66054 10-27 kg ; c = 2,9979 108
m/s ; 1 eV = 1,6022 10-19 J ; NA
= 6,022 1023 mol-1. Masse
molaire de l'uranium 235 M = 235 g/mol.
Calculer
l'énergie ( en MeV) libérée au cours d'une fission. (152,4
; 168,2 ; 176,3 ; 186,3 ; 194,3 ; aucune réponse exacte ).
Perte de masse Dm
= m(9540Zr) +m(13852Te) + 2mn -m(23592U).
Dm
=94,8860 + 137,9007 +2*1,00866 -234,9933 = -0,18928 u.
-0,189,28* 1,66054 10-27 =-3,14307 10-28
kg.
Energie libérée = |Dm| c2 =3,14307 10-28 (2,9979 108)2 =2,8248 10-11
J.
2,8248 10-11 /( 1,6022 10-19) =1,763 108 eV = 176,3
MeV.
On suppose que toutes les fissions
nucléaires de l'uranium 235 libèrent la même énergie que précédemment.
Chaque jour, le réacteur nucléaire consomme une masse m = 112 kg
d'uranium enrichi qui contient 3,0 % en mase d'uranium 235. La
puissance produite par le réacteur nucléaire est de 920 MW. Le
rendement du réacteur est défini par : h = PE
/ PN avec PE, puissance
électrique fournie et PN, puissance nucléaire
fournie par les fissions.
Déterminer
la valeur du rendement (en % ). (29 ; 31 ; 33 ; 35 ; 42 ;
aucune réponse exacte ).
Masse d'uranium 235 : 112*0,03 =3,36 kg.
Nombre de réactions de fission en une journée : 3,36 103
/ 235 * 6,022 1023 =8,61 1024.
Energie nucléaire fournie en un jour : 8,61 1024
* 2,8248 10-11
=2,4322 1014 J.
Puissance nucléare : PN =2,4322 1014
/(24*3600) =2,815 109 W = 2,815 103 MW.
h
= 920 / 2815 =0,327 ( ~ 33 %).
|
|
Lentille convergente.
le
point A d'un objet AB réel est placé sur l'axe optique d'une lentille
convergente de vergence C = 15 dioptries. AB est assimilable à un
segment perpendiculaire à l'axe optique. l'axe optique est orienté dans
le sens de propagation de la lumière. Le
centre optique de la lentille est noté O. L'mage de l'objet donnée par
la lentille est notée A'B'. A'B' est virtuelle, de même sens que
l'objet et quatre fois plus grande que l'objet.
Calculer la valeur algébrique de la distance A'A ( en cm). (-15 ; -10 ; -5 ; 10 ; 15 ; aucune réponse exacte ).
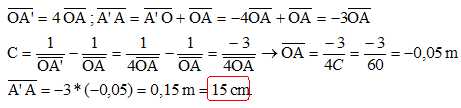
|
|