Etude d'un filet d'eau : concours technicien supérieur 2012. Ministère du développement durable des transports et du logement.

On considère un filet d'eau cylindrique vertical sortant d'un robinet en chutant librement. Chacun aura sans doute observé, si le rayon R moyen du filet d'eau est assez petit, - qu'en haut du filet, la surface extérieure, c'est à dire que le rayon du filet d'eau, noté r, varie de façon sinusoïdale autour de R. Autrement dit, et on admettra, on peut écrire à une altitude  z et à un instant t, que le rayon r du filet est de la forme r(z,t) = R +R0 cos (2pft-kz) où k est une constante strictement positive et f la fréquence de variation du rayon. - qu'en bas du filet, si celui-ci est assez long, l'eau à tendance à se décomposer en petites gouttes qui semble correspondre à une explosion du filet. Quelle est la valeur moyenne de la fonction r(z,t) au cours du temps ? La valeur moyenne de la fonction cosinus est nulle ; la valeur moyenne de la fonction r(z,t) est donc égale à R. Quelle est la plus grande valeur possile du rayon ? La plus petite ? Donner alors une condition entre R et R0 pour afirmer que le rayon oscille faiblement. La plus grande valeur du cosinus est égale à 1, d'où la plus grande valeur du rayon : R+R0. La plus petite valeur du cosinus est égale à -1, d'où la plus petite valeur du rayon : R-R0. Le rayon oscille faiblement si R0 est très inférieur à R. A partir des équations de la mécanique des fluides, on peut développer un modèle pour lequel on obtient une relation, dite de dispersion : f2 = 10-6 k2(k2R2-1) / R. Qu'est ce qu'un milieu dispersif ? Dans un milieu dispersif, la vitesse dépend de la fréquence. Quelle est la dimension de la constante k ? Quelle est son unité dans le système internationnal ? k2R2 est sans dimension ; R a la dimension d'une longueur ; k est l'inverse d'une longueur ( m-1). On admet que le filet d'eau est instable et se fragmente ( deuxième phénomène ) si la relation de dispersion ne possède pas de solutions réelles pour la fréquence f. Quelle est la condition sur k et R pour que le filet explose ? f2 , R, k2 sont positifs ; si (k2R2-1) est négatif, il n'y a pas de solutions réelles. k2R2<1 ou bien kR compris entre -1 et +1. La durée TE nécesaire à l'explosion est alors égale à 1/ |f|. Donner l'expression de TE en fonction de k, R et une constante numérique. |f |= 10-3 k[(1-k2R2) / R ]½ ; TE=1/ |f| = 103 R½ /[ k (1-k2R2)½]. On fixe la valeur de R. Quelle est, en fonction de R, la valeur kc de k permettant d'avoir le temps d'explosion le plus petit ( explosion la plus rapide ) ? On donne pour la fonction f(x) = x2(1-x2), sa dérivée f' = 2x(1-2x2).  Dans l'expression de TE, le dénominateur k (1-k2R2)½ doit être le plus grand possible. k2(1-k2R2) devant être le plus grand possible, sa dérivée  doit être nulle : 2kc(1-kc2R2) +k2(-2R2kc)= 0 ; 2kc-2kc3R2-2R2kc3= 0. 2kc(1-2R2kc2)=0 ; kc = 0 ou bien 1-2R2kc2= 0 soit kc =±1/(2½ R). Or k est strictement positif, seul la solution kc =1/(2½ R) convient. Calculer TE. TE mini=103 R½ /[ kc (1-kc2R2)½] avec R2kc2=½. TE mini=103 R½ /[0,5 kc ] avec 1/kc =2½ R. TE mini=2 *2½ 103 R1,5 . Pour R = 1 cm = 0,01 m, TE mini=2 *2½ 103 *0,011,5 =2,8 s. On montre aussi que la différence d'altitude entre deux gouttes consécutives après explosion est environ Dv = 2p/kc. Calculer Dv en centimètre et TE en seconde.On donne 2p 2½~10. Dv = 2p/kc = 2 p 2½ R = 10 R = 10 cm.   .  . 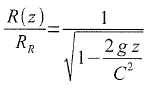Une étude plus poussée montre qu'il existe une constante C et un rayon RR, rayon du filet d'eau au niveau du robinet, tels que :  où z est l'altitude d'un point du filet d'eau et g l'accélération de la pesanteur. Quelle est la dimension de C ? 2gz / C2 est sans dimension ; C2 a la dimension de g z  ( accélération fois une distance  soit distance2 / temps2). C est une distance divisée par un temps, c'est à dire une vitesse : [C]= L T-1 ; C s'exprime en m s-1. Lorsqu'on suit une goutte d'eau du filet, comment varie son altitude au cours du temps ? Que peut-on par conséquent dire du sens de variation de la fonction R(z) lorsqu'on est de plus en plus bas dans le filet d'eau ? L'origine des altitudes est prise au sol, point le plus bas. L'altitude d'une goutte d'eau en chute, diminue donc au cours du temps. 2g z/C2 diminue et 1-2g z / C2 augmente. Par conséquent R(z) diminue. En utilisant les questions précédentes, montrer que ce modèle explique bien le premier phénomène observé. Si le filet est assez long, R(z) diminue suffisamment pour que le produit kR(z) soit inférieur à 1, ce qui conduit à l'exposion du filet en petites gouttes. .

menu