|
|
Le
principe du chauffage solaire est de faire circuler un fluide
caloporteur ( glycol ) entre des panneaux solaires chauffés par
le rayonnement solaire et une dalle.
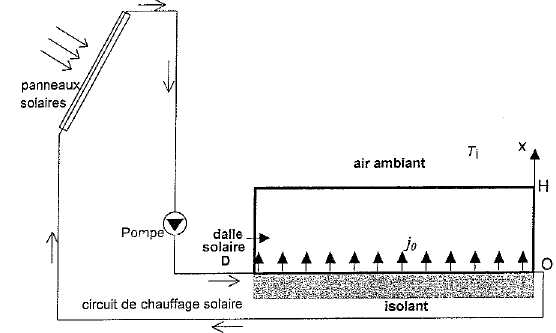
On
s'intéresse au comportement de la dalle solaire d'épaisseur H. Celle-ci
forme le plancher du rez-de-chaussée du bâtiment à chauffer ; elle est
en béton dense ( conductibilité thermique l, masse volumique r,
chaleur massique c ). La direction perpendiculaire à la surface S de la
dalle est repérée par la cote verticale x à partir du fond. Cette dalle
reçoit une densité de flux j0(t) par sa face inférieure en
x=0. Les dimensions transversales de la dalle sont très grandes devant
H, de sorte que le problème peut être supposé unidimensionnel. La
température de l'air ambiant dans le bâtiment est Ti. La face inférieure de la dalle est parfaitement isolée thermiquement.
Introduction.
Rappeler
la loi de Fourier unidimensionnelle liant la densité de flux de chaleur
j(x,t), la température T(x,t) dans la dalle et la conductivité l.
j(x,t) = -l S dT/dx.
Le vecteur densité de courant de chaleur possède le sens des températures
décroissantes, d'où le signe moins dans la loi de Fourier.
Quelle est la dimension de j ? En déduire l'unité de l.
Le flux thermique s'exprimme en watt (W) ; S s'exprime en m2 ;
l = - j(x,t) dx /(S dT) ; l s'exprime en W m-1 K-1.
En
effectuant un bilan thermique de la tranche élémentaire [x, x+dx ] de
la dalle entre un instant t quelconque et t+dt, établir les équations
différentielles vérifiées par j et par T :
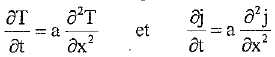
où a représente la diffusibilité thermique de la dalle, que l'on exprimera à l'aide des grandeurs physiques de la dalle. Quelle est l'unité de a ?
Flux thermique de conduction : -d j(x,t).
Puissance thermique reçue par le volume Sdx de dalle : rSdx c dT/dt.
En régime permanent : -d j(x,t) = rSdx c dT /dt ; -d j(x,t) /dx = rS c dT /dt. (1) .
Dériver l'expression de la loi de Fourier par rapport à x : d j(x,t) /dx = -l S d2T/dx2.
Repport dans (1) : l S d2T/dx2 = rS c dT /dt ; dT /dt = l /(rc) d2T/dx2 ;
a = l /(rc) ; l s'exprime en W m-1 K-1, r en kg m-3 et c en J K-1kg-1.
a s'exprime en m2 s-1.
L'échange
de chaleur par convection entre la face supérieure de la dalle et l'air
ambiant est bien représenté par la loi de Newton : j(H,t) = h [T(H,t)-Ti]
où le coefficient d'échange thermique h est considéré comme constant et uniforme sur toute la surface.
Quelle est l'unité de h ? De quels paramètres physiques dépend ce coefficient
?
h = j(H,t) / [T(H,t)-Ti] ; h s'exprime en W K-1.
h dépend des caractéristiques du fluide, de la nature de l'écoulement, de la température, de la forme de la surface d'échange...
|
.
|
Analyse dimensionnelle.
Le système est caractérisé par 8 grandeurs physiques T-Ti, j0, h, l, a,
H, x et t dont les unités sont formées à partir de 4 unités seulement (
m, s, K, W ). Daprès le théorème de Vaschy-Buckingham le probléme
physique ne dépend que de 8-4 = 4 nombres P sans dimension, dont un évident est P1 = x / H.
En écrivant une équation aux dimensions reliant les 8 grandeurs sous la forme :
(T-Ti)m j0n hp lq tu ar Hv xw =1, exprimer n,p u et v en fonction de m, q, r et w.
[(T-Ti)m ] = Km ; [j0n] = Wn ; [hp] = Wp K-p ; [lq] =Wq m-q K-q ; [tu] = su ; [ar ] = m2r s-r ; [Hv]=mv ; [ xw]= mw.
KmK-p K-q = K0 d'où m -p-q=0 (1) ; p = m-q.
WnWpWq = Wn+p+q = W0 d'où : n+p+q= 0 (2) ; (1) +(2) donne : m= -n.
m-q m2rmv mw = m-q+2r+v+w=m0 d'où -q+2r+v+w=0 (3) ; sus-r =su-r = s0 d'où u = r ; v = q -2r -w.
Montrer que les trois autres nombres sont P2 =h(T-Ti) / j0 ; P3 =at / H2 ( nombre de Fourier ); P4 =hH / l ( nombre de Biot ).
h s'exprime en W K-1 ; j s'exprime en W ; par suite h(T-Ti) / j0 est sans dimension.
a s'exprime en m2 s-1 ; H2 s'exprime en m2 ; at / H2 est sans dimension.
h s'exprime en W K-1 ; H s'exprime en m ; l s'exprime en W m-1 K-1 ; h /(H l ) est sans dimension.
En déduire l'expression du temps caractéristique td de diffusion de la chaleur à travers la dalle en fonction de H et a. A.N : H = 26 cm, a = 9 10-7 SI.
td s'exprime en seconde ; a s'exprime en m2 s-1 ; H s'exprime en m : td = H2/ a = 0,262 / 9 10-7 =7,5 104 s.
En déduire de même une longueur caractéristique Ld de diffusion au bout de 24 heures.
Ld s'exprime en mètre ; a s'exprime en m2 s-1 ; td s'exprime en seconde : Ld = a td / H.
Quelle
signification physique peut-on donner au nombre de Biot ? Quelles
hypothèses peut-on adopter pour déterminer le comportement d'un
dispositif dont le nombre de Biot est, soit très petit devant 1, soit
très grand devant 1 ?
Le nombre de Biot compare les résistances au transfert thermique à l'intérieur et à la surface d'un corps.
Une valeur du nombre de Biot supérieure à 1 signifie que la conduction
de la chaleur à l'intérieur du corps est plus lente qu'à sa surface. Un grand nombre de Biot
indique un grand gradient de température dans le solide.
Une valeur du nombre de Biot petit devant 1 ( P4 < 0,1 ) signifie
que la résistance interne est négligeable, et donc que la température
peut être considérée comme uniforme à l'intérieur du corps.
Faut-il tenir compte de l'épaisseur H dans le problème thermique étudié ? h = 6,7 SI, l = 1,75 SI, a = 9 10-7 SI , H = 26 cm.
P4 =hH / l = 6,7 *0,26 / 1,75 ~ 1. Il faut tenir compte de l'épaisseur H.
|
Régime périodique.
L'irradiation
solaire reçue par les panneaux solaires lors d'une journée de temps
clair est une fonction sinusoïdale du temps. Il en est de même en
première approximation pour le flux de chaleur émis par le circuit
solaire au fond de la dalle, de sorte que : j(0,t) = j0 ( d + sin (wt).
d est la déclinaison solaire et donc du numéro du jour dans l'année, t le temps écoulé depuis le lever du soleil, w la pulsation diurne de période J = 24 heures.
On étudie la réponse de la dalle à une sollicitation thermique j(0,t) = j0 exp(i w t), où j0 = 1 W m-2. Afin de simplifier cette étude, la dalle sera considérée comme un milieu infiniment épais.
Dans la suite des calculs, on se placera aux équinoxes.
Rappeler la définition de ce terme. Que vaut alors d ?
Aux équinoxes la durée du jour est égale à la durée de la nuit ; d = 0.
Résoudre l'équation différentielle ci-dessus.
On
pose j(x,t) = f(t). g(x), les fonctions j(x,t), f(t) et g(x) étant
supposées complexes ( méthode de séparation des variables).
dj/dt = g(x) df(t) / dt = g f ' ; d2j/dx2 = f(t)d2g(x)/dx2 = f g" ; g f ' = a f g" .
Les deux variables x et t étant indépendantes, les expressions dans
chaque membre de droite et de gauche ne peuvent de tout temps égales
que si elles sont égales à une constante arbitraire k :
g" / g = 1/a f '/ f = k.
Par suite : g"-kg = 0 (1) et f '-ka f = 0 (2).
Solutions de (1) : g(x) = Ax +B si k=0.
g(x) = A exp(k½x) + Bexp(-k½x) si k >0.
Equation caractéristique : r2-k r = 0 ;
si k >0 : solutions r1 =k½ et r2 = -k½ ; g(x) = A exp(k½x) + B exp(-k½x).
si k < 0 : solutions r1 =jk½ et r2 = -jk½ ; g(x) = A exp(j(-k)½x) + B exp(-j(-k)½x) ou encore : g(x) = A cos ((-k)½x+ B) avec A et B constants.
Or j(0,t) = j0 sin (wt), on retiendra cette dernière solution.
Solutions de (2) : f(t) = C exp(ka t) avec C une constante.
j(x,t) = AC exp (ka t) cos ((-k)½x+ B).
En déduire que l'expression de la densité de flux de chaleur j(x,t) réelle, en réponse à une solicitation sinusoïdale j1(0,t) = j0 sin (wt) est de la forme :
j1(x,t) = j0 exp(-ax) cos (wt-ax) où a est une constante positive que l'on exprimera en fonction de a et w.
Interpréter
physiquement le phénomène décrit par cette expression, et expliquer en
quoi la dalle est un milieu thermiquement dispersif.
Milieu dispersif : l'amplitude diminue avec le terme exp(-ax).
Calculer
le rapport de l'amplitude de j(H,t) à celle de la densité du flux
j(0,t), ainsi que le temps caractéristique tp de propagation de
la chaleur sur la distance H.
Amplitude de j(0,t) =j0 ;amplitude de j(H,t) = j0 exp(-aH); j(H,t) / j(0,t) = exp(-aH).
|
|