|
|
Elaboration de MoO3.
Le molybdène et ses dérivés sont extraits de la molybdénite MoS2.
Après concassage, broyage puis enrichissement par flottation ( pour
éliminer les concentrés de cuivre et de tungstène ), le minerai est
grillé à l'air dans un réacteur ( l'eau est évaporée et le soufre est
éliminé sous forme de SO2 ), selon la réaction :
MoS2(s) + 3,5 O2(g) = MoO3(s) + 2SO2(g) (1).
Calculer l'enthalpie standard de la réaction (1) à 298 K et à 700 K.
DrH° = 2DfH°(SO2(g)) + DfH°(MoO3(s)) -3,5 DfH°( O2(g)) - DfH°(MoS2(s)
DrH°298 =2(-296,8) +(-745,1) -3,5 *0 -(-235,1) = -1103,6 kJ mol-1.
On suppose les capacités thermiques molaires indépendantes de la température sur l'intervalle [298 K - 700 K ].
DrH°700 = DrH°298 + (700-298) (2Cp(SO2(g))+Cp(MoO3(s))-3,5 Cp( O2(g))-Cp(MoS2(s) )
DrH°700 = -1103,6 + 402(2*39,9 +75,0 -3,5 *29,4 -63,5) 10-3 kJ mol-1.
DrH°700 = -1103,6 -4,66 = -1108,3 kJ mol-1.
Cette réaction de grillage est-elle endo ou exothermique ?
DrH° étant négative, cette réaction est exothermique.
L'opération de grillage est réalisée en partant d'un mélange stoechiométrique de MoS2 et d'air ( 20 % de dioxygène et 80 % de diazote ), initialement à 298 K.
Quelle est la température finale TF atteinte par le mélange, compte tenu de la chaleur dégagée par le grillage isobare de MoS2 à 700 K ?
L'énergie dégagée par la combustion chauffe
les produits formés et le diazote.
Le système étant supposé adiabatique :
DrH°298 + (2Cp(SO2(g))+Cp(MoO3(s)) +14 Cp(N2) )(TF-298) =0
TF =298 -DrH°298 / (2Cp(SO2(g))+Cp(MoO3(s)) +14 Cp(N2) ).
TF =298 +1103,6 103 / (2*39,9 +75 +14 *29 ,1) =2261 K.
L'oxyde MoO3 est ensuite purifié par voie humide à l'aide de NH4OH
afin d'éliminer Cu, Ni et W sous forme de sulfures. Comme le procédé de
dépôt électrochimique ultérieur, à partir d'une phase vapeur, nécessite
l'utillisation de poudre métallique pure de molybdène, il convient au
préalable de réduire l'oxyde.
La réduction de l'oxyde MoO3 en métal Mo est réalisée grâce au dihydrogène dans un four. H2 très pur et très sec circule à contre-courant sur des nacelles recouvertes de poudre de MoO3.
L'ensemble est à la pression atmosphérique. Les opérations de réduction
sont réalisées entre 700 et 1300 K ( domaine de température pour lequel
le métal et l'oxyde sont solides, non miscibles ) en deux étapes
successives.
Vers 800 K, le dihydrogène réduit d'abord MoO3 en MoO2.
Ecrire cette réaction de réduction. Calculer la constante d'équilibre de cette réaction à 800 K.
MoO3(s) + H2(g) = MoO2(s) + H2O(g). (2)
DrG°2 = -85600-26,7 T.
DrG°2 = -85600-26,7*800 =-106 960 J mol-1.
DrG°2 = -RT ln K ; ln K = DrG°2 /( -RT) = 106960 / (8,31*800) =16,1 ; K = 9,7 106.
La réaction est exothermique et sa constante d'équilibre est très grande : elle démarre instantanément et sera totale.
|
L'étape suivante réalisée vers 1000 K, consiste en la réduction de MoO2 en Mo.
L'enthalpie libre de cette réaction vaut DrG°3 =105300-98,6 T.
Calculer la constante d'équilibre de cette réaction (3) à 1000 K.
DrG°3 = 105300-98,6*1000 =6700 J mol-1.
DrG°3 = -RT ln K3 ; ln K3 = DrG°3 /( -RT) = 6700 / (8,31*1000) =0,81 ; K3 = 2,2.
Montrer que cette dernière réaction ne peut démarrer dès la fin de la réduction de MoO3 en MoO2.
DrG°3 est positive à 1000 K : cette réaction (3) est thermodynamiquement impossible.
Calculer le nombre de moles n de H2 nécessaire pour assurer le démarrage de cette seconde réduction à partir de N moles de MoO3 présentes au départ.
MoO2(s) + 2H2(g) = Mo(s) + 2H2O(g). DrG° doit être négative.
Enthalpie libre pour la réaction : DrG° = DrH° -T DrS° ;
DrH° = N DfH°(Mo(s))+ 2N DfH°(H2O(g))-N DfH° (MoO2(s) -n DfH° (H2(g)).
DrH°3 =0 +2N(-241,8)-N(-588,9) = 105,3 N kJ.
DrS° = N S°(Mo(s))+ 2N S°(H2O(g)) -N S° (MoO2(s) -n S° (H2(g)) =28,7 N+2*188,8 N -46,3 N -130,6 n = 360 N-130,6 n J K-1.
DrG° = 105,3 N 103 -1000 (360 N-130,6 n ) J.
105,3 N -360 N + 130,6 n < 0 ; 130,6 n < 254,74 N ; n < 1,95 N.
|
Déterminer, en utilisant par exemple un tableau d'avancement, le nombre de moles de H2 nécessaire pour réduire une masse de 3 tonnes de MoO3 déposé sur les nacelles.
M(MoO3) =95,9 +3*16 =143,9 g/mo l; n(MoO3) = 3 106 / 143.9 =2,085 104 mol.
|
avancement (mol)
|
MoO3(s) |
+3H2(g)
|
= Mo(s)
|
+3H2O(g)
|
initial
|
0
|
2,085 104 |
n
|
0
|
0
|
en cours
|
x
|
2,085 104-x
|
n-3x
|
x
|
3x
|
fin
|
xmax
|
2,085 104-xmax =0
|
n-3xmax =0
|
xmax |
3xmax |
xmax =2,085 104 mol ; n = 3xmax =3*2,085 104=6,254 104 ~6,3 104 mol.
Quel(s) traitement(s) le dihydrogène excédentaire doit-il subir avant d'être injecté à nouveau dans le réacteur ?
Il faut éliminer la vapeur d'eau. Le dioxygène de l'air doit être
également éliminé : le mélange dihydrogène- dioxygène étant explosif
quasiment en toute sproportions.
Structure de MoO3.
Le trioxyde de molybdène présente à l'état solide une structure
assimilable à une structure cubique dans laquelle les atomes de
molybdène occupent les sommets et ceux d'oxygène sont positionnées au
milieu de chaque arête.
Représenter en perspective la maille de MoO3. préciser le nombre d'atome de chaque espèce appartenant à cette maille.
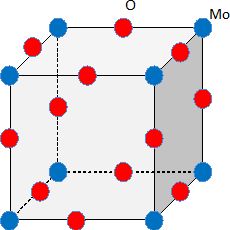
Chaque atome de molybdène appartient à 8 mailles et compte pour 0,125 : pour une maille : 8*0,125 = 1 atome Mo en propre.
Chaque atome d'oxygène appartient à 4 mailles et compte pour 0,25 : pour une maille :12*0,25 = 3 atomes O en propre.
Calculer le paramètre a de la maille, sachant que la masse volumique de MoO3 est µ=4690 kg m-3.
Volume de la maille : a3. Masse de la maille :
m =M(MoO3) / NA = 0,1439 / (6,02 1023) =2,39 10-25 kg.
a = (m / µ)1/3 =( 2,39 10-25 / 4690)1/3 =3,71 10-10 m = 371 pm.
|
Décrire le polyèdre formé par les atomes d'oxygène autour du molybdène. Est-il régulier ?
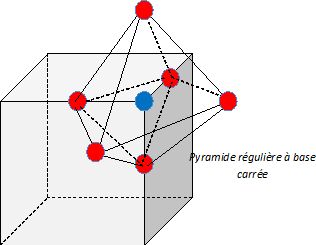
Déterminer rMo, le rayon de l'atome de molybdène en supposant le contact Mo/O réalisé sur chaque arête. rO= 130 pm.
Dans les tables, rMo~ 73 pm. Discuter de la nature de la liaison chimique dans MoO3.
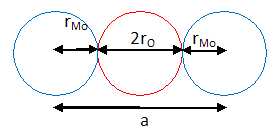
rMo = ½a -rO =185-130 = 55 pm.
L'atome d'oxygène est bien plus électronégatif que le molybdène. Les liaisons dans MoO3 ont un caractère ionique très marqué. Le rayon de l'anion O2- est supérieur à celui de l'atome d'oxygène.
Calculer le rayon maximum rM+ du cation métallique de type M+ pouvant s'insérer, soit en F, le centre d'une face, soit en C, le centre du cube, sans provoquer la déformation de la maille.
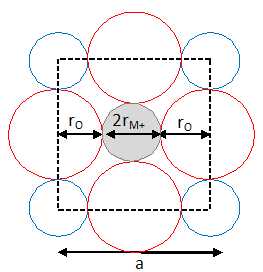 rM+ = ½a -rO =185-130 = 55 pm. rM+ = ½a -rO =185-130 = 55 pm.
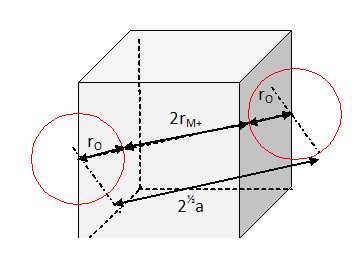 rM+ = ½2½a -rO =185*1,414-130 ~131 pm. rM+ = ½2½a -rO =185*1,414-130 ~131 pm.
Quel est le nombre maximal d'ion lithium Li+, pour lequel rLi+ = 60 pm pouvant s'insérer dans MoO3 afin de donner une structure dite bronze de molybdène, de formule LiMoO3 ?
Sans
déformation de la maille, un ion lithium peut s'insérer au centre
du cube. Cet ion est trop gros pour venir s'insérer au centre d'une
face, sans déformer la maille.
|
|




