|
|
La lunette astronomique est un système centré qui se compose :
- d'une lentille L1 de distance focale f '1 = 60 cm assimilée à une lentille mince de centre optique O1 et de diamètre D.
- d'une lentille L2 de distance focale f '2 = 10 cm assimilée à une lentille mince de centre optique O2 et de diamètre d.
La lentille L2 est située derrière lalentille L1.
Etude de la lentille L2.
Calculer sa vergence.
C2 = 1/f '2 = 1/0,10 = 10 dioptries.
Construire l'image A'B' de l'objet AB à travers la lentille L2.
Retrouver par le calcul la position de l'image. A est situé à 6,0 cm devant O2.
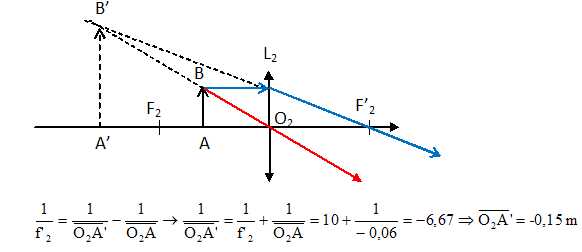
Etude de la lunette astronomique.
La
lunette est réglée de façon à donner d'une étoile ( objet à l'infini),
une image à l'infini, ce qui permet à l'observateur d'éviter toute
fatigue puisqu'il voit sans accommodation.
Nommer la lentille L1. L1 joue le rôle d'objectif.
Nommer la lentille L2. L1 joue le rôle d'oculaire.
Comment nomme-t-on un tel système optique.
La lunette est afocale.
Préciser et justifier la positions des foyers dans un tel système optique.
L'image de l'étoile, objet à l'infini, se trouve au foyer image F'1 de l'objectif et joue le rôle d'objet pour l'oculaire L2.
L'image définitive étant à l'infini, l'image intermédiaire est au foyer objet de L2.
Le foyer image de L1 est confondu avec le foyer objet de L2.
|
.
|
Construire l'image définitive.
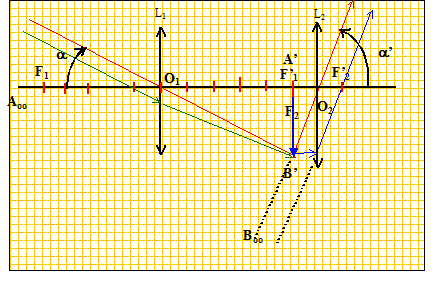
Exprimer puis calculer le grossissement G = a' / a.
tan a =
A'B'/O1F1 =
A'B'/ f'1 proche de a
radian si l'angle est petit.
tan a'
= A'B' /f'2 proche
de a'
radian si l'angle est petit.
a et a
' sont de sens contraire donc le grossissement G est
négatif : G = -
f '1 /f '2.
G = -60 / 10 = -6.
|
Etude de la lunette de Galilée.
Galilée décide de construire une lunette composée d'une première lentille convergente L1 ( f '1 = 60 cm ) et d'une seconde lentille divergente L3 ( f '3 = -10 cm ).
Construire l'image définitive.
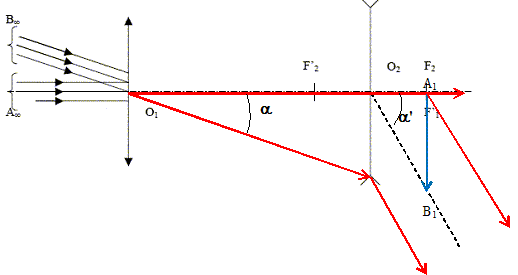
Exprimer puis calculer le grossissement G = a' / a. tan a
~a
= A1B1 /f '1 ; tan
a'
~a'
= A1B1 /|f '3| ; G =
f '1 /|f '3| =60/10 = 6.
Dans quel but, Galilée a-t-il utilisé une lentille divergente comme deuxième lentille ?
Cela réduit la longueur de l'instrument d'optique.
La
distance des deux lentilles convergentes est 70 cm ; la distance de la
lentille convergente à la lentille divergente n'est que de 50 cm.
|
|