|
|
On
se propose d'étudier le fonctionnement et les performances d'une
machine thermique ( turbine à gaz à combustion externe ) dans laquelle
un gaz que l'on supposera parfait décrit en circuit fermé les
opérations réversibles suivantes :
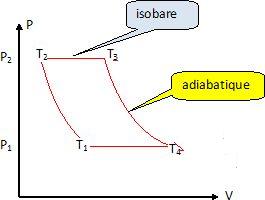
- Le gaz initialement dans l'état 1 ( P1, T1 ) traverse un compresseur dans lequel il subit une évolution adiabatique jusqu'à l'état 2 ( P2, T2 ).
- Il se trouve alors en contact avec une source chaude où il se réchauffe à pression constante jusqu'à la température T3, il est alors dans l'état 3 ( P2, T3 ).
- Le gaz pénètre ensuite dans la turbine où il se détend jusqu'à la pression P1 ; en fin de détente il est dans l'état 4 ( P1, T4 ).
- Il achève de se refroidir à la pression P1 au contact d'une source froide jusqu'à la température T1 où il se retrouve à l'état 1.
On définit la capacité thermique à pression constante du système Cp =gR / (g-1).
Tracer
en diagramme (P, V) l'allure du cycle théorique de cette machine. Faire
apparaître la température et la pression pour chaque état.
Déterminer l'énergie thermique Qc échangée avec une mole de gaz avec la source chaude en fonction de T2, T3, g et R.
Qc = Cp( T3-T2) = gR / (g-1)( T3-T2).
Déterminer l'énergie thermique Qf échangée avec une mole de gaz avec la source froide en fonction de T1, T4, g et R.
Qf = Cp( T1-T4) = gR / (g-1)( T1-T4).
En déduire le travail global W de cette mole de gaz au cours du cycle.
Lors d'une transformation adiabatique il n'y a pas d'échange thermique.
Sur un cycle l'énergie interne d'un gaz parfait ne varie pas.
par suit, le premier principe conduit à W +Qc +Qf = 0.
W = - gR / (g-1) ( T3-T2+T1-T4).
On rappelle que lors d'une trnasformation adiabatique d'un gaz parfait le produit PVg = cste.
En éduire une relation entre T, P et g.
V = RT / P ; P(RT / P)g d'où P(1-g)Tg=cste ; P Tg /(1-g) = cste. |
.
|
Exprimer les températures T1 et T4 en fonction de P1, P2, T2, T3 et g.
P1 T1g /(1-g) = P2 T2g /(1-g) ; T1 = (P2 / P1)(1-g)/g T2.
P2 T3g /(1-g) = P1 T4g /(1-g) ; T4 = (P2 / P1)(1-g)/g T3.
On pose r = P2/P1.
Exprimer le rendement théorique hth en fonction de r et g.
rendement = valeur absolue du travail récupéré / énergie dépensée à la source chaude = |W| / Qc = | (T3-T2+T1-T4)| / ( T3-T2).
hth =1-(T4-T1) / ( T3-T2).
T4-T1 =r(1-g)/g ( T3-T2) ; hth =1-r(1-g)/g.
Le rapport r étant limité par les limites de résistances de l'installation, avec lequel des trois gaz suivants obtiendra-t-on le meilleur rendement. r est supérieur à 1
gaz
|
argon
|
air
|
CO2
|
g
|
1,67
|
1,4
|
1,31
|
| 1/g-1 |
-0,401
|
-0,29
|
-0,24
|
| si r = 4,0 : 1- r(1-g)/g |
0,43
|
0,33
|
0,28
|
le meilleur rendement est obtenu avec l'argon.
|
On donne r =4,0, T1 = 300 K, T3 = 900 K.
Calculer les valeurs de T2 et T4. Dans le cas de l'argon :
T1 = r(1-g)/g T2 ; 300 = 4,0-0,401 T2 ; 300 = 0,573 T2 ; T2 = 523 K.
T4 = r(1-g)/g T3 ; T4 = 4,0-0,401 *900 ; T4 = 516 K.
Calculer la valeur du travail global au cours du cycle.
W = - gR / (g-1) ( T3-T2+T1-T4).
W = -1,67*8,314 /0,67 (900-523 +300 - 516) = -3,34 103 J pour une mole de gaz.
Calculer le rendement théorique.
Dans le cas d'un cycle de Carnot évoluant entre une
source froide à T1 et une source chaude à T3, le rendement
maximun serait égal à :
h = 1-Tfroide /Tchaude
=1-T1/T3 =1-300/900 = 0,67.
|
|