|
|
Transfert thermique.
Une pièce est séparée par un mur en brique,
d'épaisseur e=30 cm, dont l'extérieur est à -4°C et l'intérieur à 13°C.
Conductivité de la brique : l
= 0,82 W m-1 K-1 ; résistances thermiques
superficielles interne ri = 0,14 m2 K W-1
; externe re = 0,08 m2KW-1.
Calculer la
résistance thermique totale de ce mur et en déduire le coefficient d
transmission yjermique K.
R = ri + re + e/l
= 0,14 +0,08 +0,30 / 0,82 =0,5858 ~0,59 m2KW-1.
K = 1/R = 1/0,5858 =1,707 ~1,7 W K-1 m-2.
Calculer
le flux thermique par m2 de surface.
F = K(qi-qe) =1,707(13-(-4)) =29
W m-2.
Calculer
les températures de surface Ti et Te.
F = 1/ri(qi-Ti) ; Ti
= qi-Fri=13-29*0,14=8,94
~8,9 °C.
F = 1/re(Te-qe) ; Te = qe+Fre=-4+29*0,08= -1,68 ~
-1,7 °C.
Electricité.
Une station de pompage est constituée de 4 électropompes d'une
puissance unitaire hydraulique de 450 kW.
L'installation dispose également, pour les besoins auxiliaires, d'une
distribution triphasée consommant une puissance active de 50 kW
que l'on assimilera à une résistance.
On supposera qu'il s'agit d'un réseau équilibré sous un régime
sinusoïdal parfaitement linéaire.
Alimentation par réseau triphasé 230 / 400 V; 50 Hz.
Electropompe alimentée par un moteur asynchrone : tension 400 V
couplage étoile cos f = 0,7,
rendement 0,87.
Pompe centrifuge rendement 0,6.
Calculer
la puissance active, réactive consommée par une pompe.
Puissance active = puissance hydraulique /( rendement moteur *rendement
pompe).
P =450 /(0,87*0,6)=862 kW.
Puissance réactive : Q = P tan f
=862 *1,02 =879,4 ~880 kvar.
Déterminer la
puissance réactive de l'installation auxiliaire.
Cette installation étant assimilée à une résistance, ne consomme pas de
puissance réactive.
Calculer
la puissance active et réactive consommée par la station lors du
fonctionnement des 4 pompes.
Ptotal = 4*862+50=3498 ~3,5 103 kW.
Qtotal = 4*879,4 =3518 ~3,5 103 kvar.
|
.
|
Calculer la capacité
de la batterie de condensateurs à mettre en place afin de relever le
facteur de puissance à 0,9 pour les modes de couplages triangle et
étoile.
Facteur de puissance avant correction : tan f = Qtotal / Ptotal
=1,0057 soit cos f =0,705.
Après correction : tan f
=0,484.
Les condensateurs ne consomment pas de puissance active.
Q'total / Ptotal =0,484 ; Q'total =0,484*3498
=1694 kvar.
Puissance réactive consommée par les condensateurs : Qcond
=1694-3518 = -1824 kvar.
En étoile
: C = -Qcond / (U2w) avec w = 2 p f = 6,28*50 =314 rad/s et U =
400 V.
C = 1824 103 /(4002*314)=0,0363 F = 36,3 mF.
En triangle
: C = -Qcond / (3U2w) = 12,1 mF.
On retient ce couplage, car il nécessite des condensateurs de plus
faible capacité.
Hydraulique.
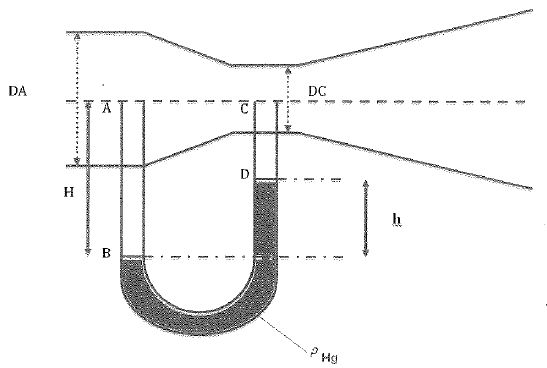
H =500 mm ; h = 200 mm ; diamètre en A : DA = 180 mm ; en C DC =30 mm ; g = 9,81 m s-2 ; rHg =13600 kg m-3 ; reau = 1000 kg m-3.
|
Exprimer puis calculer la différence de pression entre les points A et C.
A et B sont dans l'eau : pB-pA =reau H g. (1)
D et C sont dans l'eau : pD-pC =reau (H-h) g. (2)
B et D sont dans le mercure : pB-pD =rHg h g. (3)
(2)+(3)-(1) donne : pA-pC = reau (H-h) g + rHg h g -reau H g.
pA-pC = rHg h g -reau h g =hg(rHg-reau) =0,200*9,81 (13600-1000)=24721 ~2,47 104 Pa.
En déduire la vitesse vA à l'entrée du Venturi.
Théorème de Bernoulli entre A et C ( points situés dan le même plan horizontal) :
½reau v2A + pA = ½reau v2C + pC.
v2C - v2A = 2 / reau(pA- pC) = 2 10-3*2,47 104 =49,4.
Conservation du débit volumique : pD2A/4 vA = pD2C/4 vC ; vC =D2A/D2C vA =(180/30)2 vA =36 vA.
(362-1)v2A =49,4 ; vA =0,1953 ~0,20 m/s.
|
|