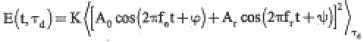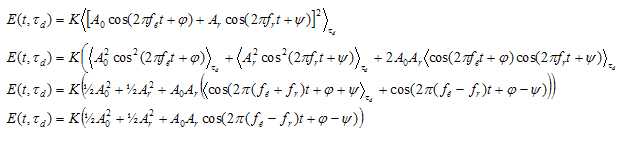|
|
On
appelle effet Doppler la modification de la fréquence des phénomènes
périodiques lorsque les systèmes échangeant des signaux ont un
mouvement relatif.
Citer une situation de la vie quotidienne dans laquelle l'effet Doppler est perceptible.
Lorsqu'une
ambulance munie d'une sirène s'approche d'un observateur
immobile, le son perçu est plus aigu ; il devient plus grave lorsque la
sirène s'éloigne.
Un radar de contrôle routier est un instrument servant à mesurer la vitesse des
véhicules. En météorologie, le radar Doppler permet d'analyser la vitesse et le mouvement
des perturbations. En imagerie médicale, le radar Doppler permet d'étudier le mouvement des fluides
biologiques.
Calcul du décalage Doppler.
Soit un objet P qui se déplace à vitesse uniforme V le long d'un axe Ox.

A
l'origine des coordonnées, se trouve un dispositif S. Ce dernier envoie
des impulsions lumineuses de fréquence précise. La vitesse de la
lumière c est indépendante du mouvement de la source. Le signal émis
est considéré comme une suite de "bips" émis à une fréquence fe dans le référentiel de S. Cette question a pour but de calculer la fréquence fr reçue par le dispositif S après rétrodiffusion sur l'objet P en mouvement.
On appelle x0 la coordonnée de P à l'instant t=0.
Donner l'équation horaire de son mouvement xP(t).
xP(t) = Vt + x0.
A l'instant t=0, S émet un bip lumineux qui voyage vers P à la vitesse c.
Calculer l'instant t1 auquel P reçoit le bip.
t1 = xP(0) / c = x0 / c.
A l'instant t = Te = 1 / fe, S émet un nouveau bip lumineux.
Calculer l'instant t2 auquel P reçoit le bip.
t2 = xP( Te) / c =Te +( V Te + x0) / c = Te + V Te / c + t1 = Te ( 1 +V / c) + t1.
Evaluer la période T = t2-t1 du phénomène "vu" dans le référentiel de P.
T = Te ( 1 +V / c).
P
rediffuse les signaux qu'il reçoit. Il s'agit d'un processus pour
lequel l'émission s'effectue avec la même période T que la réception.
Une portion du signal est ainsi rétrodiffusé vers S.
Calculer la fréquence fr alors reçue par S dans son référentiel et montrer que fr ~(1-2V/c) fé.
Après réflexion sur P, S reçoit un signal de période T = Te ( 1 +V / c)2.
Or fr = 1/ T = fé / ( 1 +V / c)2 = fé ( 1 +V / c)-2.
Or V / c << 1 d'où : fr ~ fé ( 1 -2V / c).
Exploitation de ce décalage.
Afin
de mesurer la vitesse d'un écoulement on y injecte de petites
particules servant de traceurs. Le processus de rétrodiffusion a lieu
sur ces particules. Le signal utilisé est dans le domaine visible le = 514,5 nm.
Si l'écoulement a une vitesse de l'ordre d'une dizaine de mètres par seconde, estimer l'ordre de grandeur de ce décalage Doppler en fréquences. Commenter cette valeur.
( fr - fé ) / fé ~ -2V / c ~ -2*10 / (3 108) ~ 7 10-8.
fé = c / lé =3 108 / (514,5 10-9) = 5,83 1014 Hz ; |fr - fé |~ 3,9 107 Hz.
Ce décalage est trop petit pour être directement exploitable.
|
.
Afin d'obtenir un résultat exploitable, on effectue le montage suivant :
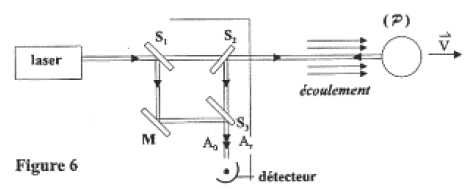
La lumière issue du laser arrive sur une première lame séparatrice S1 qui " divise" le faisceau en deux parties. Une première partie, qui traverse S1, arrive sur une deuxième lame séparatrice S2. Cette lame, ainsi que la lame S3, ont les mêmes propriétés que S1. Pour la lumière issue de S2, on ne représente toutefois que le faisceau partiellement transmis qui va se réfléchir sur la particule P, revenir sur S2 et se réfléchir en direction de S3,
la traversant jusqu'au détecteur. Avant d'atteindre le détecteur, ce
rayon rejoint celui qui avait été réfléchi initialement par S1 puis par le miroir parfait M et enfin la lame semi-transparente S3
qui réalise, en définitive, la recombinaison des rayons. Avant de
rejoindre le détecteur, les amplitudes respectives de ces deux rayons
superposées valent :
Ar cos ( 2pfrt +Y) et A0 cos ( 2pfét +j).
Dans le contexte de cette expérience, le déétecteur reçoit donc une superposition du signal émis à la fréquence fé ( chemin S1-M-S3), qui n'a subit aucun changement de fréquence et du signal reçu à la fréquence fr ( chemin S1-S2-P-S2-S3 ), modifiée par effet Doppler. Il convertit ce signal lumineux en signal électrique suivant l'opération :
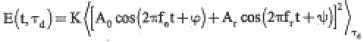
K est une constante multipicative et le détecteur moyenne sur son temps d'intégration td.
Comparer les grandeurs td et 1/(fé-fr).
td est de l'ordre de quelques nanosecondes ; 1/(fé-fr) = 1/ (3,9 107) ~2,6 10-8 s ~26 ns.
1/(fé-fr) et td sont du même ordre de grandeur.
En déduire que : E(t, td) = ½K(A02 +A2r +2A0Ar cos ( 2p(fé-fr)t +j-Y)).
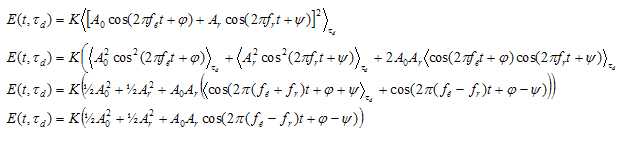
La moyenne de la fonction cos2 est égale à ½ ; la moyenne de la fonction cosinus est nulle ; il n'est pas utile moyenner cos ( 2p(fé-fr)t +j-Y) car 1/(fé-fr) et td sont du même ordre de grandeur.
On
réalise une expérience au cours de laquelle on enregistre un décalage de
fréquence 38,89 MHz avec un laser d'émission de longueur d'onde le = 514,5 nm.
Quelle est donc la vitesse d'écoulement étudié ?
( fé - fr ) / fé ~ 2V / c ; V = ( fé - fr ) c /(2 fé ) ~ 38,89 106 *3 108 / (2*5,83 1014) =10,0 m/s.
La mesure de fréquence est précise à 0,1 % près.
c et fé étant suffisamment précis, la précision sur la vitesse est de l'ordre de 0,1 %.
|
|