|
|
Un
pont à haubans est un pont suspendu dont le tablier T est soutenu par
de gros câbles en acier tendus sur des pylônes placés aux extrémités.
Pour mesurer avec précision les déformations du tablier soumis à
différentes contraintes, on émet une impulsion laser à partir du lidar
mobile solidaire de T placé au point M. Le système optique est
pointé en direction de miroirs réflecteurs appelés " coins de
cube" fixés sur la paroi extérieure d'un satellite parfaitement
stationnaire S. Ces miroirs renvoient la lumière qu'ils reçoivent vers
l'émetteur muni au point M, d'un détecteur d'impulsions. La mesure de
l'écoulement de temps t écoulé entre l'émission et la réception du
signal en M, permet de déterminer la longueur du trajet optique
correspondant, parcouru par les rayons lumineux à la vitesse c = 2,998
108 m/s.
.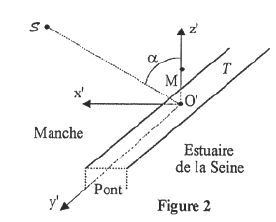
Lorsque le pont est au repos et qu'il nest soumis à aucune contrainte,
T est donc horizontal. L'angle a
vaut 56°.
Le pont ne porte aucune charge sur T. Le temps mis par la lumière pour
effectuer l'aller-retour entre M et S est t0 = 0,246 s.
Calculer
la distance D= SM.
D = ½c t0 =0,5 *2,998 108 *0,246 = 3,6875 107
~3,69 107 m.
Le pont est soumis à différentes contraintes au cours desquelles on
effectue des mesures de t, que l'on compare à la durée de référence t0.
T est chargé de camions en vue d'évaluer sa déformation verticale : M
se déplace le long de l'axe O'z' jusqu'au point Mv. On note tv,
la valeur prise par t. tv-t0 = 5,8 10-9
s.
Montrer
que 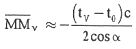 . Faire l'application
numérique. . Faire l'application
numérique.
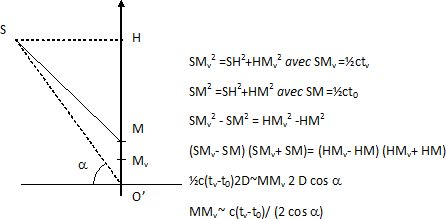
MMv
~2,998 108*5,8 10-9 /(2 cos 56) =1,554 ~1,6 m.
( en senc contraire de l'axe O'z').
Pour tester la résistance du pont à une déformation latérale que peut
provoquer une tempète, un remorqueur de haute mer est ammaré au
tablier, aux environs du point M. Le bateau exerce une traction ( 106
N). M se déplace suivant O'x' jusqu'au point ML. On note tL
la valeur prise par t. tL-t0 = -1,7 10-9
s.
Calculer MML.

MML
~2,998 108*1,7 10-9 /(2 cos
56) =0,456 ~0,46 m. ( dans le sens de l'axe O'x').
La précision sur la mesure de t équivaut à la durée de l'impulsion laser t = 50 10-12 s.
L'incertitude sur |tv-t0| vaut 2 t.
Quelle est
l'incertitude sur MMv ?
c est
suffisamment précise ; l'incertitude relative sur a est supposé être proche de 2%.
Incertitude relative : dMMv
/ MMv = da / a + d|tv-t0| /
|tv-t0| =0,02 +100
10-12 / (5,8 10-9) =0,037.
Incertitude
sur MMv
: 0,037*1,554 = 0,057 m ~ 6 cm.
La mesure de la déformation du pont est fiable.
|
Les rayons lumineux de longueur d'onde l0 = 532 nm, issus du
système lidar sont émis dans un cône de demi-angle au sommet ß = 2 10-5
rad. On souhaite évaluer un aspect énergétique de cette expérience
réalisée en télémétrie. A chaque impulsion émise, une énergie lumineuse
Eé, uniformément répartie dans le cône de demi-angle au
sommet ß, est envoyée par l'émetteur vers S distant de D du lidar.
On considère la réflexion sur un "coin de cube" de surface apparente s
( surface du coin de cube telle qu'elle est vue par un rayon
provenant du lidar ). Le miroir se comporte comme une ouverture
diffractante plane, éclairée sous incidence normale et il réfléchit
totalement l'énergie E' qu'il reçoit.
On considère que cette énergie lumineuse, réfléchie à une distane D, se
répartit par diffraction, à l'intérieur d'une tache centrale carrée de
côté 2l0D / s½.
Ainsi, après l'émission d'une impulsion d'énergie Eé, une
énergie ET est recueillie ,en retour, par le détecteur du
lidar dont l'ouverture collectrice de lumière a un diamètre F0 = 0,5 m.
On néglige les pertes à la réflexion ainsi que l'influence de
l'atmosphère et on admet que la totalité de la lumière diffractée est
uniformément répartie dans la tache centrale de diffraction, supposée
beaucoup plus grande que la surface de l'ouverture du détecteur.
Calculer
l'aire de la surface éclairée par le faisceau émis par le lidar à une
distance D de celui-ci et en déduire le rapport E' / Eé.
L'énergie lumineuse
Eé est uniformément répartie dans le cône de demi-angle au
sommet ß.
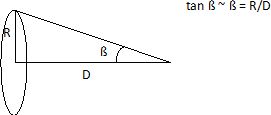
Surface de base de ce cône : S = pR2
= p (D ß)2.
Le rapport des énergies est égal au rapport des aires. E' / Eé =
s / S = s /(p (D ß)2).
E' / Eé =0,01 / (3,14*(3,69 107 *2 10-5)2 =5,8 10-9.
Calculer
le rapport ET/E'. On donne
s = 1 cm2.
Aire de la tache de diffraction ( carré de côté 2l0D / s½) : S' =(2l0D)2 / s. Aire de l'ouverture du
collecteur : S" = p F02/4.
ET / E' = S" / S' = s p F02/( 4(2l0D)2).
ET / E' = 10-2 *3,14*0,52 /
(4 (2*532 10-9 *3,69 107 )2) =1,27 10-6 .
Exprimer
enfin ET / Eé en fonction des
données.
ET / Eé
= ET / E' *E' / Eé = s p F02/( 4(2l0D)2) *s /(p (D ß)2) = s2F02/( 4(2l0D)2 (D ß)2).
L'énergie d'un photon dépend de la longueur d'onde. Ici l'énergie du
photon vaut 3,73 10-19 J.
Calculer
l'énergie minimale nécessaire pour détecter en retour un photon.
ET / Eé =5,8 10-9 * 1,27 10-6 = 7,4 10-15.
Eé = 3,73 10-19 / 7,4 10-15 = 5,0 10-5 J.
Si le rétroréflecteur est composé d'une mosaïque carrée de n "coins de
cube", par
quel facteur est multipliée l'énergie reçue par les miroirs donc celle
reçue par le détecteur ?
La surface des miroirs est équivalente à un seul miroir diffractant de
surface n fois plus grande que celle de chaque "coin de cube" dont elle
est constituée.
Le rapport des énergie est égal au rapport des surfaces. L'énergie
reçue est multipliée par le facteur n.
Mesure de la distance terre-lune.
Un faisceau laser est dirigé vers des panneaux de rétroréflecteurs
posés sur la lune. Afin de coder les signaux émis, le laboratoire
utilise une séquence bien précise. Les impulsions lumineuses sont
envoyées par trois à des intervalle de temps de 1,65 ns entre la
première et la deuxième et de 2,50 ns entre la deuxième et la troisième
impulsion. Cela permet, à la réception, de distinguer les signaux qui
ont réellement parcouru un aller-retour terre-lune de certains signaux
détectés de manière accidentelle.
Les différents rayons
lumineux émis par le laser sont supposés uniformément répartis dans un
cône de demi-angle au sommet ß = 2 10-5 rad. Le faisceau renvoyé par la lune présente un élargissement dû à la diffraction identique à celui mentionnée ci-dessus.
Estimer,
pour une réflexion sur un miroir "coin de cube", la fraction de
l'énergie lumineuse, émise depuis la terre, qui est récupérée à son
retour par un détecteur.
On néglige à nouveau les effets dus à l'atmosphère. s = 1 cm2 ; s' = 1,8 m2 (surface du détecteur) ; D=3,9 105 km, distance terre-lune.
Une puissance par unité de surface s'exprime en W m-2.
E' / Eé =
s / S = s /(p (D ß)2).
E' / Eé =0,01 / (3,14*(3,9 108 *2 10-5)2 =5,2 10-11.
ET / E' = s s' /( 2l0D)2= 0,01*1,8 / (2*532 10-9 *3,9 108 )2 =1,04 10-7 .
ET / Eé =1,04 10-7 *5,2 10-11 = 5,4 10-18.
Le laser émet à chaque impulsion, une énergie lumineuse E = 0,3 J.
Quel est le nombre moyen de photons arrivant sur le détecteur à chaque impulsion après un aller-retour terre-lune ?
ET = 0,3 *5,4 10-18 =1,63 10-18 J.
Energie d'un photon : 3,73 10-19 J
Nombre de photons reçus : 1,63 10-18 / (3,73 10-19 )=4,4 ~ 4 photons.
Un réflecteur est composé d'une centaine de "coins de cube". Quel est le nombre moyen de photons reçus ? 4,4 102.
Une expérience donne une valeur du temps t nécessaire aux photons pour effectuer un aller-retour de 2,584 s.
Calculer plus précisément la distance terre-lune.
D = ½ct = 0,5*2,998 108 *2,584 =3,873 108 m.
Le temps est mesuré avec une précision de 10 ps.
En déduire l'erreur absolue sur la mesure de D.
c est connue avec suffisamment de précision. L'erreur relative sur le temps est donc égale à l'incertitude relative sur D.
dD / D = dt / t = 10 10-12 / 2,584 =3,7 10-12.
Erreur absolue sur D : 3,7 10-12* 3,873 108 = 1,5 10-3 m.
Que dire du nombre de chiffres significatives de la valeur numérique 2,584 s.
On aurait pu donner un plus grand nombre de chiffres significatifs sur la valeur de t et sur la valeur de c.
Pour arriver à de telles précisions, de nombreux paramètres doivent
être parfaitement maîtrisés. Parmi eux la mesure du temps est une
donnée fondamentale.
Quel est, selon vous, l'instrument qui permet à l'observatoire de faire une mesure très précise du temps ?
Une horloge atomique.
Quelles peuvent être les erreurs introduites par l'atmosphère ?
La célérité de la lumière dans l'air est un peu inférieure à la célérité de la lumière dans le vide.
L'atmosphère absorbe une partie des photons.
|
|

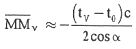 .
. 

