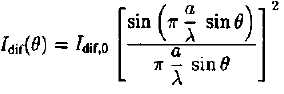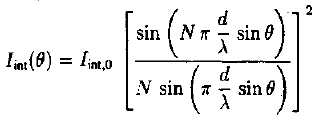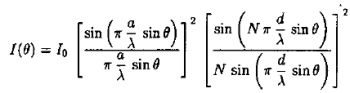|
|
Le transducteur ne peut pas
générer un faisceau parfait d'ultrasons.
On se propose d'étudier des techniques permettant d'améliorer la
résolution des images échographiques.
Impossibilité
d'isoler un rayon lumineux.
Expliquer
pourquoi il n'est pas possible expérimentalement un rayon lumineux
( infiniment fin ).
Dès
lors qu'une fente a une largeur de l'ordre de grandeur de la longueur
d'onde de la lumière, on observe un phénomène de diffraction..
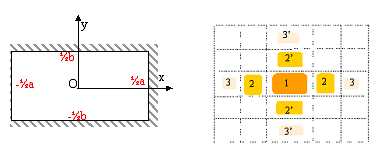
On considère dans cette question une onde lumineuse monochromatique de
longueur d'onde l arrivant
sous incidence normale sur une fente rectangulaire centrée en O et de
côtés a et b.
Représenter
la figure de diffraction obtenue sur un écran.
 . .
Résolution
latérale d'un tansducteur à un élément.
le transducteur est une source de surface rectangulaire de côté a = 1,5
mm et b = 1 cm.
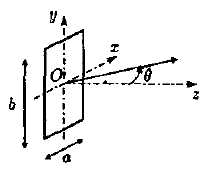
On
admet que l'onde ultrasonore qu'il émet est identique à celle obtenue
par diffraction d'une onde ultrasonore de même fréquence à travers une
fente rectangulaire de côtés a et b. le transducteur émet des ultrasons
de fréquence n = 3 MHz et de
longueur d'onde l = 0,497 mm
dans le milieu biologique.
Calculer
numériquement l'ouverture angulaire du faisceau ultrasonore
parallèlement au petit côté a ( c'est à dire dans le plan xOz). Faire
de même pour le grand côté b et conclure.
q1 = l / a = 0,497 / 1,5 = 0,33 rad. q2 = l / b = 0,497 / 10 ~ 0,05 rad.
La longueur de la fente est
trop grande pour provoquer la diffraction.
Un
calcul théorique donne l'expression suivante de l'intensité acoustique Idif(q) générée par le transducteur
rectangulaire suivant la direction q dans le plan xOz, avec Idif 0
une constante positive.
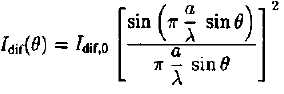
L'allure du diagramme de
rayonnement du transducteur, représentant l'intensité acoustique émise
en fonction de la direction q
est donnée. On remarque l'existence de plusieurs lobes : le plus
important, suivant la direction q=0,
est appelé lobe principal et les autres sont appelés lobes secondaires.
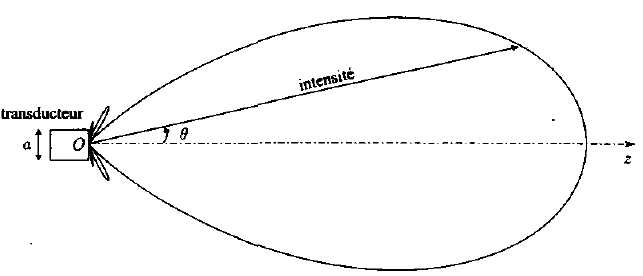
Les ultrasons émis présentent une directivité matérialisée par la
largeur angulaire du lobe principal.
Comment
faut-il choisir l et a pour améliorer
la directivité du transducteur ?
Pour
améliorer la directivité, il faudrait éviter la diffraction sur
l'ouverture du transducteur tout en ayant un faisceau assez fin. Pour
"a" fxé à 0,5 mm, en augmentant la fréquence on diminue la longueur
d'onde, c'est à dire q.
Le choix précédent peut-être à l'origine de fausses images ou
d'artéfacts très génant en échographie médicale. Pourquoi ?
Les lobes secondaires se trouvent dans les directions définies par :
pa / l sin q = ±(2k+1) p/2 ; sin q = ± l/(2a) (2k+1)p avec k entier.
A "a " fixé, en diminuant l,
on fait croître le nombre de lobes secondaires.
Montrer
que le choix l = 0,497 mm et a =
0,4 mm permet d'éviter ces problèmes. En contre-partie, quel est
l'inconvénient de ce choix ?
l/(2a) =0,497 / 0,8 =0,621.
p = 0, lobe principal ; p = ±1,
sin q
= ± 1,86 , sin q > 1, pas lobe secondaire.
Il y a pas de lobes
secondaires, mais le faisceau est peu directif.
|
Résolution
latérale d'un transducteur multiéléments.
Por
améliorer la directivité du faisceau d'ultrasons, on utilise un
transducteur multiéléments. Il est constitué de N = 11 éléments
rectangulaires équidistants, séparés par une distance d = 0,7 mm, et de
propriétés identiques à l'élément étudié ci-dessus. Chaque élément est
alimenté par un signal électrique identique :les ondes émises par les
différents éléments sont par conséquent en phase les unes avec les
autres.
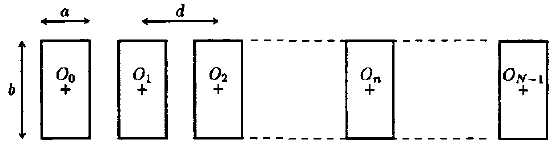
Dans
un premier temps, on ne tient pas compte de la largeur a" de chaque
élément. On assimile le transducteur à une suite de N éléments
rectilignes équi-espacés repérés par les points O0, O1,...
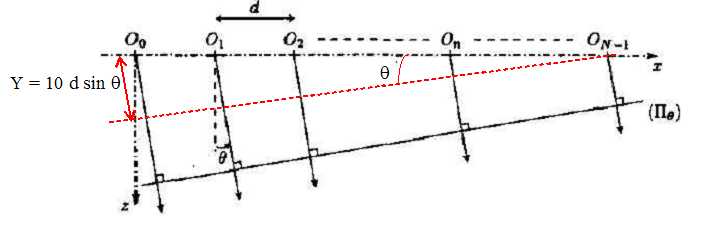
On s'intéresse aux ondes émises dans le plan xOz dans une direction q avec l'axe Oz. On note P0 un plan orthogonal à
cette direction.
L'onde issue de O0 arrive en retard par rapport à celle
issue de On au niveau du plan P0.
Calculer
le décalage temporel tn au
niveau de ce plan, de l'onde issue de O0 par rapport à celle
issue de On
en fonction de n, d, q et c.
Y = n d sin q ; tn
= Y/c = n d sin q / c. ( n
varie de 0 à N-1 = 10 ).
L'amplitude acoustique complexe An(q) de l'onde émise
par l'éément n dans la direction q
est définie de sorte que : An(q) = A0 exp[ i 2p c / l tn], n variant de 0 à
N-1.
On admet que l'intensité acoustique Iint(q) , résultant des interférences
entre les diverses ondes, est : Iint(q) =[A0(q) + A1(q) +....+AN-1(q)]2.
|
Montrer
que l'intensité acoustique totale se met sous la forme : 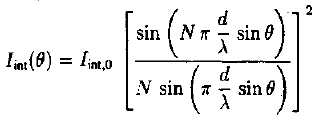
On pose A = p / l d sin q . An(q) = A0
exp[ i 2p c / l tn] = A0
exp[ i 2p / l n d sin q] = A0 exp(i2An).
Iint(q) =A20(q) [1+ exp(i2A)+ exp(4iA)
+....+ exp(2(N-1)iA)]2.
Il s'agit de la somme d'une suite géométrique de premier terme 1, de
dernier terme exp(2(N-1)iA), de raison q= exp(i2A).
Somme de cette suite : premier terme fois (1-qn) / (1-q)
=[1-(exp(i2A)N] / (1-exp(i2A) = [1-(exp(i2NA)] / (1-exp(i2A).
1-(exp(i2NA) = 1 - cos(2NA) - i sin (2NA) ; 1-exp(i2A) =1 - cos(2A) - i
sin (2A)
Modules correspondants : [ [1 - cos(2NA)]2 + sin2
(2NA)]½ =[2(1-cos(2NA)]½ = 2 sin(NA).
de même[ [1 - cos(2A)]2 + sin2 (2A)]½
=[2(1-cos(2A)]½ = 2 sin(A).
Iint(q) =A20(q) [ sin(NA) / sin(A) ]2.
Représenter
l'allure de la courbe Iint(q) / Iint(0) en fonction de
sin q.
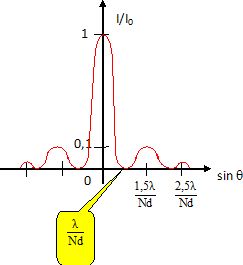
Les maximas correspondent aux interférences constructives.
|
On tient compte de la largeur a de chaque
élément du transducteur. En posant I0,
une constante :
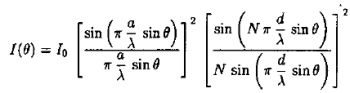
L'allure de la fonction
I / I0 est représentée :
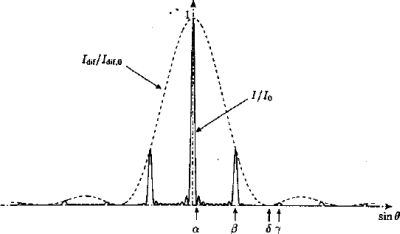
Préciser
les expressions de a, ß, g et d en fonction de l, N,d et a.
Vérifier que les
ultrasons se décomposent en seulement trois faisceaux.
l = 0,497 mm ; N = 11 ; d = 0,7 mm ; a =
0,4 mm.
a est tel que : Np / l d sin q = p ; a = sin q = l / (Nd) =0,497 / (11*0,7) =0,0645 ; q = 0,064 rad. ( 3,7 ° ).
ß est tel que: Np / l d sin q = 3/2 p ; b = sin q = 1,5 l / (Nd) = 1,5 *0,497 / (11*0,7) = 0,0968 ; q = 0,097 rad ( 5,6 °).
g est tel que: Np / l d sin q = 5/2 p ; g = sin q = 2,5 l / (Nd) = 2,5 *0,497 / (11*0,7) =0,161 ; q = 0,162 rad ( 9,3 °).
d est tel que : p / l a sin q = p ; d = sin q = l / a= 0,497 / 0,40 = 1,24 ( impossible le
sinus est compris entre -1 et 1 ).
L'amplitude du pic
secondaire situé en ß vaut 0,045 fois l'amplitude du pic central ;
celle du pic situé en g vaut 0,016. |
|


 .
.