|
|
Plan incliné.
Le wagon de queue d'un train se détache alors qu'il aborde une côte à
la vitesse V0= 30 m/s. La masse du wagon et des voyageurs
est de 170 tonnes, la voie fait un angle de 10° avec 1'horizontale. Les
roues du wagon sont freinées par un frottement solide d'intensité
constante F = 221 kN. Une fois immobilisé, le wagon redescend.
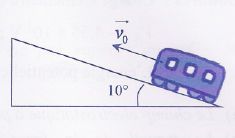
g sin 10 ~1,7 m s-2 ; 172 =289 ; 4*17 = 68 ;
51/17 = 3 ; 221/170=1,3 ; 170/221 ~ 0,77.
Le frottement solide est présent lors de la montée et de la descente
avec la même intensité.
Données :
a) L'unité du Newton est kg.m-1.s-2. Faux.
Une force est une masse
fois une accélération : kg m s-2.
b) Le wagon va s'arrêter au bout d'environ 10 secondes. Vrai.
Sur un axe parallèle au plan et dirigé vers le haut :

c) Le travail du poids est moteur lors de la descente. Vrai.
d) Lors de la descente, la valeur de l'accélération du wagon est de 3
m.s-2. Faux.
Sur un axe parallèle au plan et dirigé vers le
haut :
Station
spatiale internationale :
La station spatiale internationale (ISS) est en
orbite circulaire autour de la Terre à une altitude h = 400 km. Sa
vitesse est constante et égale à V = 7,7 km.s-1. On note G
la constante de gravitation universelle.
Données :
Rayon de la Terre: RT = 6,4 x 103 km ; Masse de
la terre : MT = 6,0 x 1024 kg.
43/7,7 = 5,6 ; 6,8 / (2p) =
1,1 ; 145 / 7,7 = 19 ; 2p /6,8
= 0,92 ;7,7 /145 = 0,053 ; 2p*6,8
=43 ;
p 6,82
= 145 ; 43*7,7 = 331 ; 145*7,7 = 1,1 103 ; 7,7 / 43 = 0,18.
a) La station possède une accélération centripète a =V2 / (RT+h).
Vrai.
b) La troisième loi de Kepler s'applique en prenant l'altitude h comme
demi-grand axe de la trajectoire. Faux.
... en prenant h + RT
comme demi-grand axe de la trajectoire.
c) La troisième loi de Kepler s'écrit, dans ce cas : T3 / (RT+h)2
= 4p2 /(GMT).
Faux.
T2
/ (RT+h)3 = 4p2
/(GMT).
d) La période de révolution de 1'ISS est T=5,6 x
103s. Vrai.
La station décrit la
circonférence 2p(RT+h)
à la vitesse V en T seconde.
T = 2p(RT+h) / V =2*3,14
(6,8 106) / (7,7 103)= 43 103 / 7,7 =
103 / 0,18 =5,6 103 s.
|
.
|
Canon à
électron.
Les électrons pénètrent en A (potentiel VA) dans un
champ électrostatique uniforme E qui permet de les accélérer et
ressortent au point B (potentiel VB).On suppose que la
vitesse d'entrée au point A est quasi nulle. L'électron n'est soumis
qu'à la force électrostatique F conservative à l'intérieur du canon. On
note d la longueur de la zone d'interaction. Lorsque l'électron arrive
au point X (potentiel Vx), sa vitesse est vx.
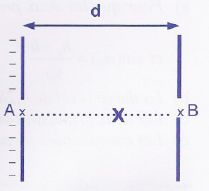
d
Données :
Charge élémentaire e = 1,60 x 10-19C; Masse de l'électron m
= 9,11 x 10-31kg ;
VA = - 4,55 x 103 V ; VB = 0 V ;
d = 10,0 cm ; 4,55 x l,60 / 9,11 =0,800.
L'énergie potentielle électrique d'une charge q en un point A est Ep(A)
= qVA.
a) Le champ électrostatique a pour valeur E = 455 V m-l. Faux
E = |VA-VB|
/ d = 4,55 103 / 0,100 =4,55 104
V m-1.
b) Le travail de la force électrostatique F, lorsque l'électron se
déplace de X à B, est W = e(Vx-VB). Faux.
W = -e(VX-VB).
c) A une constante près, l'énergie mécanique de l'électron au point X
est Em(X) =½mvx2 -eVx. Vrai.
d) La vitesse au point B est vB=2,00 x 107 m.s-l.
Faux.
Conservation de l'énergie
mécanique : ½mvB2
-eVB = ½mvA2 -eVA.
vB2
=-2e/mVA
; vB = (2e/mVA)½ =(2*1,6 10-19
* 4,55 103 / 9,11 10-31)½
=(2*0,8 1015)½ =4,0 107
m/s.
.
|
|
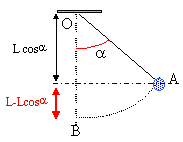
Oscillations d'un pendule.
Un pendule simple, de masse m et de longueur L, est lâché sans vitesse initiale, d'un angle a0=
30° (point A) avec sa position d'équilibre. On négligera tous les
frottements. L'origine des énergies potentielles et des altitudes est
prise au point B.
Données : L = 2,0 m ; m = 50 g ; g = 10 m s-2 ; cos 30 = 0,87 ; 1,3½ =1,14 ; sin 30 = 0,50.
a) L'énergie mécanique est égale à 130 J. Faux.
Em = mgL(1-cos a0) =0,050 *2,0 *10 (1-0,87) =0,13 J.
b) Le point A est à l'altitude ZA= 26 cm. Vrai.
zA =L(1-cos a0) = 2,0(1-0,87) = 0,26 m = 26 cm.
c) La vitesse au point B est VB= 2,28 m/s. Vrai.
Conservation de l'énergie mécanique : ½mvB2 = 0,13 ; vB2 = 0,26/0,05 = 5,2 ; vB ~(5,2)½ = (1,3*4)½ = 1,14*2 = 2,28 m/s.
d) Si le pendule avait été lâché avec une vitesse initiale de 2,0 m.s-1, l'énergie mécanique aurait été augmentée de 100 J. Faux.
½mv2 = 0,5 *0,05 * 2,02 = 0,10 J.
|
|