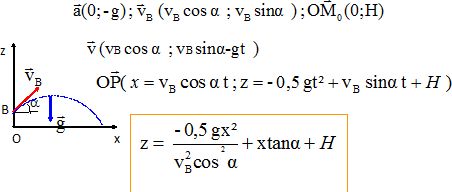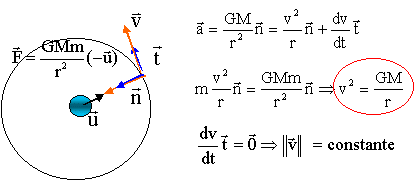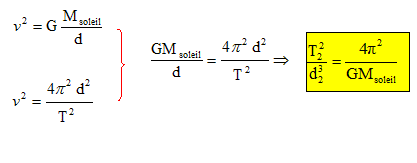|
|
Le skieur.
Un
skieur enfant glisse sur une piste inclinée d’un angle α = 20° par
rapport à l’horizontale suivant une trajectoire rectiligne. La masse de
l’ensemble est de M = 34 kg.
A t = 0 s, le skieur se laisse glisser sans vitesse initiale de la
position x= 0 m et se met en recherche de vitesse. On considère que
l’ensemble des forces de frottements sont opposées au vecteur vitesse
et sont constantes. Elles ont pour valeur F= 102 N.
Données : g = 10 m.s-2 ; cos 20 = 0,94 ; sin 20 = 0,34 ; 342
= 1156 ; 34 x 9,4 = 320.
a) Le mouvement du skieur est un mouvement rectiligne uniformément
accéléré. (Vrai ).
b) La valeur de l’accélération a = 6,4 m.s-2. ( Faux ).
Ecrire
la seconde loi de Newton sur un axe parallèle au plan et orienté vers
le bas du plan :
Mg sin a -F = M ; a =
g sin a -F/M =10 *0,34 -102
/ 34 =3,4 -3,0 = 0,40 10-2 m s-2.
c) Le skieur
parcourt depuis l’origine la longueur L = 180 m en une durée de 30 s. (Vrai ).
x = ½at2
=0,5 *0,4 * 302 = 180 m.
d) Dans une zone de la piste où la valeur des frottements est modifiée
et devient égale à 115,6 N, la quantité de mouvement du skieur est
constante. (Vrai ).
a = 3,4 -115,6 / 34 = 0. Le mouvement est
rectiligne uniforme. le vecteur vitesse et en conséquence le vecteur quantité de
mouvement sont constants.
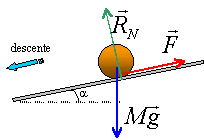
Luge.
Un enfant
tire avec une force de valeur constante F = 20 N une luge de masse m=
5,0 kg à l’aide d’une corde faisant un angle α = 20° par rapport à la
piste enneigée. L’inclinaison de la piste est égale à β = 10° par
rapport au plan horizontal. Il existe des frottements entre les patins
et la neige matérialisés par une force constante f . Le mouvement est
rectiligne et uniforme.
Données : g = 10 m.s-2 ; 30 sin 10 ~ 5 ; 30 sin 20 ~ 10 ; 30
cos 10 ~ 29,5.
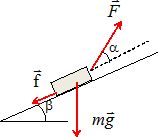
a) Lors de la montée, le travail du poids est moteur. ( Faux ).
Le travail du poids est
moteur en descente.
b) Sur une distance parcourue par la luge de AB = 30 m, la variation
d’énergie potentielle de pesanteur vaut ΔEpp ~ 250 J. (Vrai
).
ΔEpp = mg DH = mg AB sin b =5,0*10*30 sin 10 = 250 J.
c) La
force de frottement a pour valeur f ~ mg sin a. ( Faux ).
Projection de la somme
vectorielle des forces ( nulle dans le cas d'un mouvement rectiligne
uniforme )sur un axe parallèle au plan orienté vers le haut du plan.
-mg sin ß -f + F cos a = 0 ; f = F cos a -mg sin ß.
d) Le
travail des frottements sur le trajet AB est W( f ) = mgABsinß-
FABcosa. ( Vrai ).
W(f) = f AB cos 180 = - f
AB = -AB ( F cosa - mg sinß) = mgABsinß- FABcosa.
|
.
|
Projectile.
Une balle est lancée dans le champ de pesanteur uniforme d’un point B
avec une vitesse initiale B v faisant un angle α = 60° par rapport au
plan horizontal, vers un but. On considère que la balle est en chute
libre. L’énergie potentielle de pesanteur de référence est : Epp(O)
= 0 J.
Données : OB = H = 1,0 m ; VB = 10 m.s-1 ; cos 60
= 0,5 ; m = 0,10 kg ; g = 10 m.s-2 ; sin 60 =3½/2.
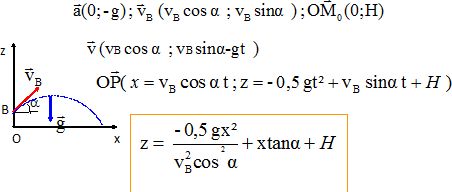
a) Dans les conditions de l’exercice, les forces de frottements ne sont
pas négligeables. ( Faux ).
La balle en chute libre
n'est soumise qu'à son poids, les frottement sont négligés.
b) L’énergie mécanique en B a pour valeur : Em(B) = ½ mVB2.(
Faux ).
Energie cinétique + énergie
potentielle de pesanteur =½ mVB2+
mgH.
c) Le sommet de la trajectoire a pour valeur Zmax =2,75 m. (
Faux ).
Au sommet la composante
verticale de la vitesse est nulle : t = vB
sin a / g.
Repport dans l'expression
de z : zmax = -0,5 g (vB sin a / g)2 +vB
sin a (vB sin a / g) + H =½(vB sin a )2/ g + H.
zmax =0,5 (10 sin 60 )2
/ 10 +1,0 = 4,75 m.
d) L’équation de la
trajectoire est z = H-x tan a
-½g( x / (VB cos a))2.
( Faux ).
Satellite
de Saturne.
Le mouvement des satellites de Saturne dans le
référentiel Saturnocentrique est considéré comme étant circulaire.
Chaque satellite se trouve sur une orbite de rayon r.
Données : G ~ 6.10-11 S.I. ; p ~ 3 ; le rapport r3/T2
= constant = 1,0.1015 S.I.
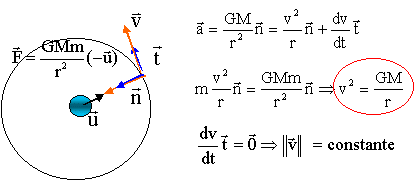
a) L’accélération d’un satellite de Saturne est
toujours radiale et centripète. ( Vrai ).
b) La valeur de la vitesse d’un satellite autour de Saturne est donnée
par (GM/r)½. ( Vrai ).
c) G s’exprime en m3.kg.s2. (Faux ).
G est une force fois une
distance au carrée divisée par le carré d'une masse.
Une force est une
masse fois une distance divisée par le carré d'un temps.
[G] = M L T-2
L2 M-2 = L3M-1T-2.
d) D’après les données, la masse de Saturne est M ~6,0.1026
kg. ( Vrai ).
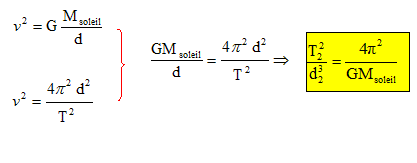
4 p2 / (GM) = 1,0
10-15 ; M =4 p2 / (G 10-15) ~4*9 /(6 10-26) ~6,0.1026 kg.
|
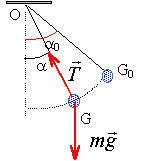
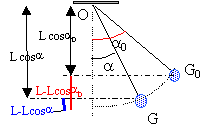
Pendule.
Une masse
m = 50 g est accrochée à une extrémité d’un pendule simple de longueur
L = 40 cm. On écarte la masse d’un angle θ = 60° et on le lâche sans
vitesse initiale dans le champ de pesanteur terrestre g = 10 m.s-2.
On néglige tout frottement. O est l’origine des positions.
Données : sin 60 = 0,87 ; cos 60 = 0,50 ; tan 60 = 1,73 ; π ≈ 3 ;
La référence de l’énergie potentielle de pesanteur est : Epp(0)
= 0
a) La période propre du pendule T ~ 1,2 s. ( Vrai ).
T = 2 p (L/g)½ = 6 (0,40 / 10)½ =1,2 s.
b) La vitesse au passage à la position d'équilibre est v0 =
gL(1 – cos 60). ( Faux ).
|
|
|
travail des forces :
La tension est toujours
perpendiculaire à la vitesse : cette force ne travaille pas.
Le travail du poids est
égal à : mg ( zG-zG0). La position d'équilibre est prise comme
origine des altitudes.
Energie
mécanique initiale = énergie potentielle de pesanteur = mg L (1-cos a0).
Energie mécanique au passage à la position d'équilibre = énergie
cinétique maximale = ½mv02.
Conservation de l'énergie mécanique : g L (1-cos a0) = ½v02.
v0=(2g L (1-cos a0))½
=(2*10*0,40(1-0,5))½ =2 m/s.
c) L’énergie
mécanique du pendule est Em = 0,25 J. ( Faux ).
mg L (1-cos a0)
= 0,050 *10*0,40(1-cos 60) = 0,10 J.
d) L’altitude
maximale atteinte par le pendule est zmax = 0,20 m. ( Vrai ).
zmax =L
(1-cos a0)= 0,40
(1-0,5) =0,20 m.
|
|
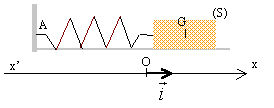
Oscillateur.
Un ressort de masse négligeable, à spires non jointives, de constante
de raideur k, est posé sur un plan horizontal sur lequel il peut se
déplacer sans frottement. Son extrémité A est fixe, son extrémité B est
reliée à un objet
ponctuel de masse m = 50,0 g. On rappelle que l’énergie potentielle
élastique d’un ressort est Epe = ½ kx2.
L’origine O du repère coïncide avec la position de repos du centre
d’inertie B du solide. Ecarté de sa position d’équilibre, le solide est
abandonné sans vitesse initiale et repasse par O avec une vitesse v0
= 2,0 m.s-1.
a) L’énergie potentielle élastique du dispositif est proportionnelle à
x. ( Faux ).
b) xmax = vmax ( k/m)½. ( Faux ) .
Energie mécanique initiale =
énergie potentielle élastique = ½kxmax2.
Energie mécanique au passage à
la position d'équilibre = énergie cinétique maximale = ½mvmax2.
Conservation de l'énergie
mécanique : ½kxmax2=
½mvmax2
; xmax2=
m / k vmax2.
c) L’énergie cinétique maximale vaut Ecmax = 1,0 J. ( Faux ).
Ecmax
=Epemax = ½mvmax2= 0,5 * 0,050 *2,02
=0,10 J.
d) Lorsque l’énergie potentielle élastique vaut 1/4 de l’énergie
mécanique alors x =½xmax. ( Vrai ).
½ kx2
= 0,25 ½mvmax2=0,25 ½kxmax2
; x2
=0,25 xmax2 ; x = 0,5 xmax.
|