|
|
Onde le long
d’une corde.
On étudie la propagation d'une perturbation le long d'une corde 1
élastique.
À la date t = 0 s, le front de la perturbation quitte l'extrémité S de
la corde.
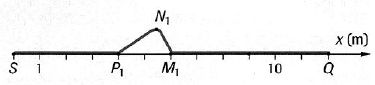
À la date t1= 2,4 s, on prend une photographie instantanée
de la corde ; la figure ci-dessous reproduit le cliché (simplifié)
obtenu avec une échelle des longueurs.
a) L’onde se
propageant le long de la corde est une onde longitudinale.( Faux )
La déformation est
perpendiculaire à la direction de propagation : onde transversale.
b) La célérité de l’onde a pour valeur 2,5 m.s-1.(Vrai )
Le front de l'onde
parcourt SM1 = 6,0 m en 2,4 s : 6,0 / 2,4 = 2,5 m/s.
c) Le point Q cesse d’être perturbé à la date t2 = 4,8 s.( Faux )
Le front de l'onde atteint Q en : 12 /2,5
=4,8 s.
d) Dans les mêmes conditions d’expérience (même force de tension), mais
en remplaçant la corde 1 par
une autre dont la longueur est deux fois plus importante et la masse
deux fois plus faible, la célérité augmente.(Vrai )
La masse linéïque de la corde est divisée
par 4. La célérité est inversement proportionnelle à la racine carée de
µ : la célérité double.
Effet Doppler.
Une sirène
d’une ambulance émet des « bips » très brefs à intervalles de temps
réguliers T. Chaque bip donne naissance à un signal sonore qui se
déplace dans l’air à la célérité V = 340 m.s-1. L’ambulance
se déplace avec un mouvement rectiligne uniforme de vitesse constante U
= 72 km.h-1 vers un observateur fixe O.
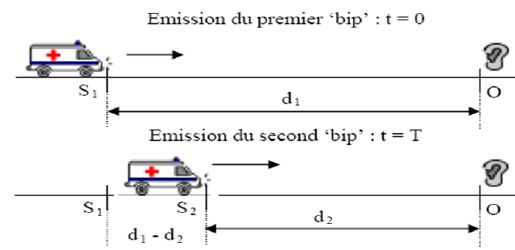
a) La date t1 correspondant à la réception du premier « bip
» a pour expression d1/V. ( Vrai )
b) La date t2 correspondant à la réception du deuxième « bip
» a pour expression T-d2/V. ( Faux ).
L'ambulance se trouve à
la distance d2 =d1- U T de O lors de
l'émission du second "bip".
Le son parcourt la distance d2 en t2 = T+d2/V.
c) La durée entre les deux
« bips », notée T0, est T0= T(1-U/V). (
Vrai )
t2 -t1 =T0 = T+d2/V-d1/V = T +(d2-d1) / V
=T -UT / V =T(1-U / V).
d) Si les
bips sont remplacés par une onde sonore de fréquence f = 400 Hz, la
fréquence perçue par l’observateur est f0 = 425 Hz. (
Vrai )
f0 = 1/T0
; f = 1/T d'où : f0
= f /
(1-U/V) avec U = 72 / 3,6 = 20 m/s.
f0 =400 / (1-20/340) = 425 Hz.
|
.
|
Rayonnements
électromagnétiques.
1) Milieu interstellaire.
L’espace entre les étoiles est loin d’être vide. Il est rempli de gaz,
principalement de l’hydrogène et de l’hélium, mais aussi des agrégats
solides (glaces, minéraux, composés organiques ou inorganiques) : la
poussière. Certaines parties de ce milieu interstellaire sont plus
denses et forment des nébuleuses. Les étoiles (et leurs planètes)
naissent d’ailleurs de ces nuages célestes. Les étoiles, les astres
ainsi que ce milieu interstellaire sont capables d’émettre des
rayonnements de fréquences différentes les unes des autres.
2) Rayonnements détectables
depuis la Terre.
La Terre reçoit de toutes les directions de l’espace des rayonnements
électromagnétiques ainsi qu’une pluie de particules qui constituent le
rayonnement cosmique. Si ce flot ininterrompu n’était pas en grande
partie arrêté par l’atmosphère, ses effets destructeurs interdiraient
toute vie. Ces rayonnements et ces particules sont les seuls supports
des informations qui nous parviennent de l’Univers (distances,
vitesses, constitution des étoiles ou des autres objets célestes).
Dans la deuxième moitié du XXème siècle, l’invention du radiotélescope
(qu’on positionne dans les déserts), sur le modèle du radar, puis la
possibilité d’envoyer des télescopes spatiaux au-delà des couches
denses de l’atmosphère, ont permis aux astronomes d’exploiter beaucoup
plus largement le domaine des ondes électromagnétiques.

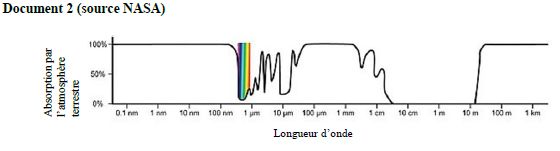
En utilisant le texte et les documents on peut
affirmer que :
a) Le domaine des longueurs d’onde visibles par l’homme est compris
entre 1000 nm et 10000 nm. ( Faux ).
Le domaine visible
s'étend de 400 à 800 nm.
b) Une onde de longueur d’onde λ ~1mm est absorbée en grande partie par
notre atmosphère. (Vrai ).
c) Les radiotélescopes peuvent étudier, depuis la terre, toutes les
ondes radios issues des astres. ( Faux )
d) Les télescopes spatiaux permettent d’exploiter certains
rayonnements, par exemple les rayonnements UV. (Vrai ).
|
Propriétés
des ondes.
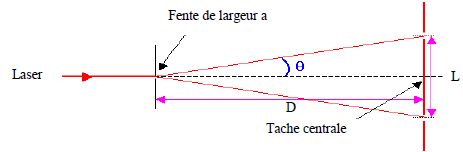
Données :
6,3/2,50 = 2,52 ; 2,5/6,3 = 0,40 ; 2,5 x 6,3 = 15,75
On oriente un faisceau laser 1 de longueur d’onde λ1 = 630
nm sur une fente verticale de largeur a1 = 0,10 mm. Sur un
écran situé à une distance D1 fixe de la fente, on observe
une tache centrale de largeur L1 = 2,5 cm.
a) Le phénomène observé sur l’écran est un phénomène d’interférences. (
Faux ).
Diffraction par une fente.
b) Si on diminue la largeur de la fente a, la largeur L de la tache
centrale diminue. ( Faux ).
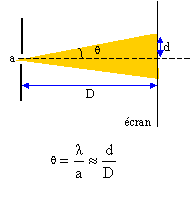 d =½L ~ l D/a ; L = 2lD/a. d =½L ~ l D/a ; L = 2lD/a.
c) L’écart angulaire (ou
demi largeur angulaire) θ = 6,3. 10-4 rad. ( Faux ).
630 10-9 / (0,1 10-3) ~630 10-5 ~6,3 10-3
rad.
En remplaçant le laser 1 par un laser 2 de longueur d’onde λ2
dans le dispositif précédent, on observe une tache de largeur L2
= 2,0 cm.
d) La longueur d’onde du laser 2 est λ2 = 504 nm. ( Vrai ).
L2
/ L1 = l2/l1
; l2 = l1L2
/ L1 =630 *2,0 / 2,5 =504 nm.
|
|
Interférences
lumineuses.
Deux fentes fines verticales parallèles, distantes de a = 0,50 mm, sont
placées à une distance D = 1,0 m d’un écran E. Elles se comportent
comme des sources S1 et S2 émettant des ondes
lumineuses synchrones de fréquence f = 4,80.1014 Hz. Données
: c = 3,00.108 m.s-1 ; aide au calcul : 100/16 =
6,25.
a) Les ondes lumineuses émises ont une longueur d’onde λ1
égale à 550 nm. ( Faux ).
l = c / f =3,00.108
/(4,80.1014 ) =6,25 10-7
m = 625 nm.
b) Au point O, intersection entre l’axe horizontal et l’écran, les
interférences sont constructives. ( Vrai ).
c) Sachant que la différence S2M – S1M = 1,25 cm,
alors les interférences au point M sont destructives. ( Faux ).
1,25 10-2 / (6,25 10-7
) =2,0 104. La différence de marche est un multiple de la
longueur d'onde : interférences constructives.
d) Avec des ondes lumineuses synchrones de longueur d’onde λ2
= 590 nm, l’interfrange i séparant les franges d’interférences vaut i =
1,18 mm. ( Vrai ).
i = l2 D /a = 590
10-9 *1,0 / (0,5 10-3) =1,18 10-3 m =
1,18 mm.
|





