|
|
Effet Doppler.
Un patient est emmené d'urgence à l'hopital dans
une ambulance signalant sa présence par une sirène émettant un son pur
de fréquence F0 ; sa route est ouverte par un motard
se déplaçant à la même vitesse. Un automobiliste stoppe son véhicule
pour favoriser le passage de l'ambulance ; quand elle s'approche de
l'automobiliste, celui-ci perçoit un son aigu qui devient plus grave
lorsqu'elle s'éloigne.
L'onde sonore émise par
l'ambulance :
A) est périodique et sinusoïdale. Vrai. ( le son émis est pur ).
B) est une onde progressive à une dimension. Faux. ( le son se propage dans toutes les
directions qui lui sont offertes ).
C) se propage avec un transport de matière et un transport d'énergie.
Faux. ( pas de transport de matière
).
D) présente une périodicité spatiale valant v/F0 avec v :
célérité du son dans l'air. Vrai.
E) n'est pas diffractée par un obstacle de taille 20 cm si la longueur
d'onde est de 50 cm.Faux. ( l'obstacle
a une dimension de l'ordre de grandeur de la longueur d'onde, il y a
donc diffraction).
Le patient entend le son de
la sirène avec un niveau d'intensité sonore L = 50 dB. Que vaut
l'intensité sonore I ( W m-2 ) dans l'ambulance ? ( 10-17
; 2 10-14 ; 5 10-11 ; 10-7 ; aucune
réponse ).
I=I0
10L/10 = 10-12
* 105 = 10-7
W m-2.
Quel est le niveau d'intensité sonore total dans l'ambulance si le
motard déclenche lui aussi sa sirène dont le niveau d'intensité sonore
est aussi de 50 dB lorsqu'elle fonctionne seule ? ( 50 dB ; 53 dB ; 57
dB ; 100 dB ; aucune réponse ).
Les intensités sonores
s'ajoutent : Itotal = 2 10-7 W m-2.
Ltotal = 10 log (Itotal) / I0)
= 10 log (2 10-7 / 10-12)
= 10 log 2 + 50 = 53 dB.
On s'intéresse à l'effet Doppler relatif au son émis par l'ambulance.
On note VS la vitesse de l'ambulance et v la célérité du son
dans l'air avec VS << v.
A) le motard perçoit le son de la sirène avec une fréquence inférieure
à F0. Faux. ( le motard
roule à la même vitesse que l'ambulance ).
B) le motard perçoit le son de la sirène avec une fréquece F0.
Vrai.
C) le motard perçoit le son
de la sirène avec une fréquence supérieure à F0. Faux.
D) la fréquence perçue par l'automobiliste à l'approche de l'ambulance
est F = (v+VS)F0. Faux. ( cette expression n'est pas homogène
).
E) la fréquence perçue par
l'automobiliste à l'approche de l'ambulance est F = (v-VS)/
v F0. Faux. ( Le son
perçu étant plus aigu, F doit être supérieure à F0 ).
|
.
|
Echographie.
Une sonde , lémetteur et de récepteur, envoie une impulsion ultrasonore
de faible durée dans le crâne du patient ; l'onde sonore s'y propage et
s'y réfléchi dès qu'elle change de milieu. Les signaux réfléchis
génèrent des échos qui, au retour sur la sonde, y engendrent une
tension brève ; un oscilloscope permet la détection de
l'impulsion émettrice et des divers échos formant l'échogramme.

Quelle est la durée Dt de l'aller-retour de l'onde
ultra-sonore dans chacun des hémisphères ?
E1
: écho dû à la réflexion sur l'entrée de l'hémisphère 1 ; E2
: écho dû à la réflexion sur la séparation des hémisphères ; E3
: échos dû à la réflexion sur la sortie de l'hémisphère 2.
Dt1 =
130-10 = 120 µs ; Dt2
= 270-130 = 140 µs.
D'après
le résultat de la question 1, la présence d'une tumeur est-elle
vérifiée par l'examen ? Si non, Pourquoi ? Si oui, dans quel hémisphère
est-elle localisée ? Justifier.
La tumeur doit se située dans l'hémisphère droit, la durée Dt2 étant bien
supérieure à Dt1.
En l'absence de tumeur les hémisphères auraient à peu près la même
taille et les durées Dt
seraient voisines.
On s'intéresse à la largeur L de l'hémisphère gauche ; on suppose que
la célérité des ultrasons est v = 1500 m/s pour l'ensemble des milieux
traversés.
Quelle
est la relation entre L et Dt ?
L = ½V Dt = 0,5 *1500 *140 10-6
=0,105 m.
Evaluer
la largeur de l'hémisphère gauche sous la forme L ±DL.
L'incertitude sur la largeur est DL
=L p(Dt) avec p(Dt) =précision relative sur la
durée Dt = 2,5 %.
DL =0,105 *0,025
=2,6 10-3 m. L = (0,105 ±2,6 10-3 ) m.
|
Scanner X.
Les
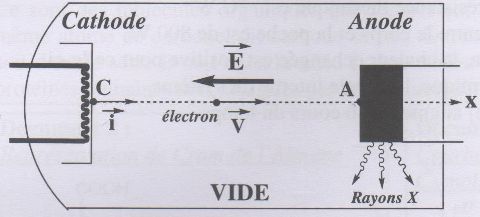
scanners X utilisés en imagerie médicale dérivent des tubes de
Coolidge. Ils sont constitués d'une cathode C et d'une anode A séparées
par une distance L et entre lesquelles on impose une différence de
potentiel électrique VA-VC = U >0. Lorsque la
cathode est portée à haute température, elle émet des électrons avec
une vitesse négligeable ; ces électrons se déplacent ensuite vers
l'anode grâce au champ électrique E crée par la tension U. Les RX émis
par le tube sont produits à l'anode suite à l'interaction des électrons
avec les atomes de celle-ci ; ces interactions se traduisent par une
conversion de l'énergie cinétique en énergie radiative ( émission de
photons ).
On notera : m : masse de l'électron, e : charge élémentaire ; c :
célérité de la lumière dans le vide ; h : constante de Planck.
Le poids des électrons est négligeable devant la force électrostatique.
Le mouvement est étudié suivant un axe horizontal orienté dans le sens
du mouvement et dont l'origine coïncide avec la cathode ; la
masse de l'électron reste inchangée pendant le déplacement.
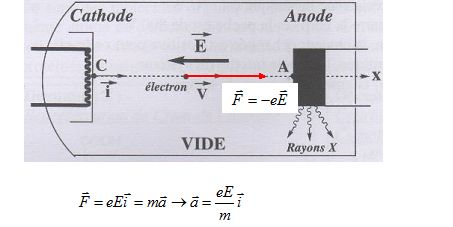
Etablir l'expression
vectorielle de l'accélération avec m, e, E et le vecteur unitaire.
Référentiel d'étude ; référentiel terrestre supposé galiléen.
En
déduire la nature du mouvement rectiligne de l'électron.
L’accélération étant constante, le mouvement est rectiligne
uniformément accéléré.
Etablir
l'équation horaire de la vitesse de l'électron en fonction de t, m, e
et E.
La vitesse est une primitive de l'accélération et la vitesse initiale
étant nulle, la constante d'intégration est nulle.
v(t) = at = eE / m t.
Etablir l'équation
horaire de la position de l'électron en fonction de t, m, e et E.
La position est une primitive de la vitesse et la position initiale
étant nulle ( origine de l'axe ), la constante d'intégration est nulle.
x(t) = ½at2 = ½eE / m t2.
Décrire
l'évolution des énergie potentielle électrique et mécanique, cinétique
de l'électron lors du déplacement de C vers A.
L'énergie cinétique initialement nulle croît.
L'énergie potentielle électrique ( Epe = -e V ) varie de -eVC
à -e VA : DEpe
= e( VC-VA ) =-e U. Cette forme d"énergie décroît.
La force électrostatique étant conservative, l'énergie mécanique de
l'électron se conserve.
EM =-eVC = ½mv2A
-e VA ou encore ECA=½mv2A =e( VA-VC ) =e U.
Exprimer
la longueur d'onde associée à l'électron en fonction de m ECA et h.
l = h / p = h
/(mvA) ; 2 mECA=m2v2A =p2.
l = h / (2 mECA)½.
Exprimer
la longueur d'onde du photon émis, suite à la conversion totale de
l'énergie cinétique de l'électron incident dans l'anode, en énergie
radiative en fonction de h, c et ECA.
ECA = h c / l0
; l0 = h c / ECA.
|
|
Transferts
thermiques.
Les
antécédents médicaux du patient révèlent qu'un intervention
chirurgicale par anesthésie générale doir être évitée. En effet, ce
patient souffre d'une anomalie musculaire génétique qui, lors d'une
précédente intervention, a provoqué une hyperthermie maligne
peranesthésique. Cette hyperthermie s'est manifestée par une hausse
brutale de la température interne de son corps de 37 °C à 40 °C.
On s'interesse aux transferts thermiques par conduction, convexion et
rayonnement.
A) un milieu matériel est nécessaire pour chacun de ces transferts
thermiques. Faux. ( le rayonnement
ne nécessite pas de milieu matériel ).
B) la convection est le seul mode provoquant un déplacement global de
matière. Faux.
C) chacun des trois transferts thermiques peut être observé dans un
milieu solide. Vrai.
D) le corps rayonne de la chaleur vers l'extérieur mais la réciproque
est fausse. Faux.
Pour
traiter cette hyperthermie, l'équipe médicale utilisa, entre autres,
des poches de glace à 0°C. On s'interesse au flux thermique échangé par
conduction entre le corps du patient et la poche de glace ; on suppose
les températures constantes et respectivement égales à 40°C et 0°C. On
rappelle l'expression du flux thermique par conduction F = DT/R où R est la résistance
thermique du corps = 5 10-2 SI.
A) l'unité de la résistance
thermique dans le système internationnal est : °C W-1. Faux.
( K W-1).
B) le flux thermique échangé par conduction entre le corps et la poche
est 800 W. Vrai.
F = 40 / 0,05 = 800 W.
C) si on prend pour référence la poche de glace, la chaleur échangée
est positive pour celle-ci. Vrai.
La glace reçoit de la chaleur.
D) si on ne considère que ce seul transfert thermique, l'énergie
interne du système thermodynamique [patient-glace] augmente au cours du
temps. Faux.
Laser.
A) pour qu'un photon
incident puisse déclencher une émission stimulée, son énergie doit être
supérieure ou égale à l'énergie libérée pendant cette désexcitation
stimulée. Faux.
B) l'effet laser ne peut pas être interprtéé en utilisant l'aspect
ondulatoire de la lumière. Faux.
C) un laser continu ou à impulsions permet une concentration spatiale
de l'énergie. Vrai.
D) un laser permet d'obtenir un faisceau de lumière
quasi-monochromatique. Vrai.
Le laser utilisé émet une lumière de puissance P= 5 mW ; elle provoque
une coagulation de la tumeur lorsque sa température passe de 37°C à 57
°C. La masse de la tumeur est estimée à 5 g ; on suppose que sa
capacité calorifique masique est proche de celle de l'eau : c ~ 4
J K-1 g-1.
A) l'énergie interne s'apparente à l'énergie mécanique à l'échelle
microscopique. Faux.
B) En valeur absolue, la variation de l'énergie interne de la tumeur
est environ 400 J. Vrai.
DU=mcDT = 5*4*(57-37) = 400 J.
C) l'énergie interne de la tumeur a diminué à l'issue de cette
opération. Faux.
D) la destruction de la tumeur est réalisée après 1 min 20 s. Faux.
Dt = DU / P =400 / (5 10-3)
=8 104 s.
|


