|
|
Le
monte-charge est équipé d'un moteur à courant continu. Les pertes du
moteur autres que par effet Joule seront négligées dans cette partie.
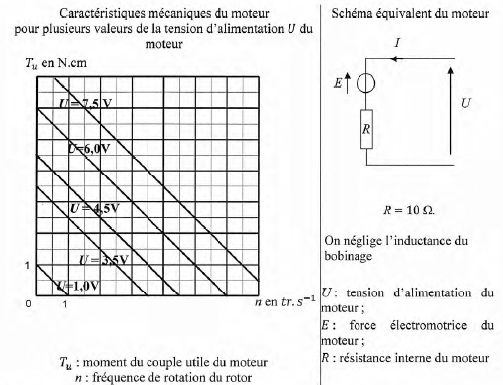
Pour une intensité du courant électrique traversant le moteur, I = 0,10
A et une tension d'alimentation du moteur U = 6,0 V, calculer la force
électromotrice du moteur.
U = E+RI ; E = U-RI = 6,0-10*0,1 = 5,0 V.
On donne l'expression du théorème du moment cinétique projeté suivant
l'axe de rotation du moteur :
Jdw/dt = Tu-Tr.
J : moment d'inertie du moteur par rapport à l'axe de rotation ( kg m2).
w : vitesse
angulaire du moteur ( rad/s).
Tr : norme du moment d'un éventiel couple résistant ( N m ).
La charge impose à l'arbre du moteur un couple résistant de moment Tr
= 0,010 N m. La charge est initialement immobile dans le référentiel du
laboratoire.
Quelle
est la relation entre Tr et le moment du couple utile
si la charge reste fixe ? Justifier.
Si la charge reste fixe, la vitesse angulaire du moteur est constante,
nulle et dw/dt est nulle. Par
suite Tu = Tr.
Déterminer
graphiquement la tension d'alimentation U à appliquer.
Pour une charge fixe, w=0 et
de plus Tu = 0,01 Nm = 1 N cm. Le graphe indique U = 1,0 V.
On se place en régime permanent et la charge est animée d'un mouvement
rectiligne uniforme à la vitesse v souhaitée dans le référentiel du
laboratoire.
Quelle
est la relation entre le moment du couple résistant et le moment du
couple utile ? Justifier.
La vitesse angulaire est constante dans un
mouvement uniforme : dw/dt
est nulle. Par suite Tu = Tr.
Compléter,
à partir du graphique, le tableau ci-dessous dans lequel n est la
fréquence de rotation du moteur et U la tension d'alimentation de ce
dernier.
U(V)
|
U0=1
|
3,5
|
4,5
|
6
|
7,5
|
n(tr/s)
|
0
|
2,5
|
3,5
|
5
|
6,5
|
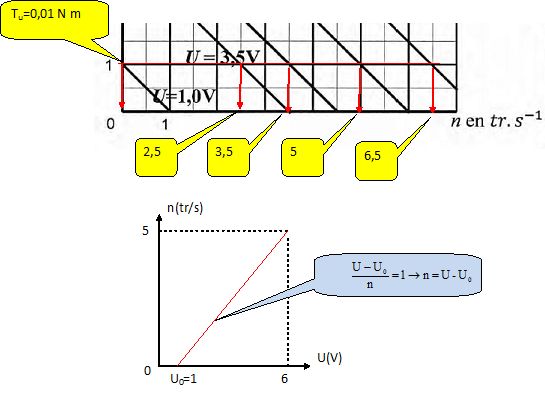
Pour ce couple résistant de moment Tr = 0,01 Nm, on mesure
pour différentes vitesses v, une unique intensité pour le courant
électrique I constante de valeur I0 = 0,10 A.
Exprimer
n uniquement en fonction de E.
D'une part : n = U-U0 = U-1.
D'autre part : U = E+RI = E+10*0,1 = E+1.
Par suite n= E.
|
.
|
Etude de
l'alimentation électrique.
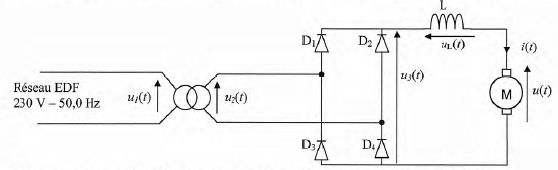
Pour le système réel, l'alimentation du moteur est réalisée par
l'intermédiaire d'un pont à 4 diodes supposées parfaites. Le pont est
alimenté par un transformateur de rapport de transformation m = 0,030.
Une bobine d'inductance L et de résistance interne supposée nulle,
misse en série avec le moteur, lisse le courant d'intensité i(t). On
note I0 la valeur moyenne de i(t). L'inductance L est
suffisante pour que l'amplitude des variations de l'intensité i(t)
autour de I0 puisse être considérée comme négligeable.
u2(t) = U2max
sin(wt). On note T la période
du signal u2(t).
Calculer
la valeur efficace U2 de la tension u2(t).
U2 = U1 m =230 *0,030 =6,9 V.
Calculer w.
w = 2 p f = 2*3,14*50 =314 ~3,1 102
rad/s.
Préciser
le rôle du pont de diode.
A partir d'une tension sinusoïdale, le pont
de diode permet d'obtenir une tension variable mais toujours positive.
L'intensité du courant qui traverse le moteur a toujours le même sens.
Indiquer pour chaque
diode, son intervalle de temps de conduction pendant une période T.
Entre 0 et ½T, les diodes D1 et D4 sont
passantes, les diodes D2 et D3 sont bloquées.
Entre ½T et T, les diodes D1 et D4 sont bloquées,
les diodes D2 et D3 sont passantes.
Tracer sur votre
copie les courbes u2(t) et u3(t).
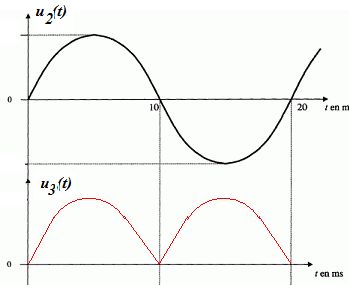
Exprimer
la tension uL(t) aux bornes de la
bobine en fonction de l'intensité i(t). Montrer que la valeur
moyenne de u(t), notée <u(t), vérifie en régime permanent
<u(t)> = <u3(t)>.
uL(t) = L di(t)/dt.
<uL(t)> = L <di(t)/dt>. Or <di(t)/dt> = 0.
Additivité des tensions : u3(t) = uL(t) + u(t).
<u3(t)> = <uL(t)> + <u(t)>.
Par suite : <u3(t)> = <u(t)>.
Montrer
que <u(t)>= 2U2max / p.
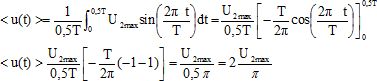
Calculer
<u(t)>.
<u(t)> = 6,9*1,414 *2/3,14= 6,2 V.
|
|
Isolation
acoustique du moteur.
Les
pertes énergétiques liées au frottement solide sont en partie
converties en énergie acoustique. La mesure du niveau d'intensité
acoustique, noté L, exprimé en dBa est faite à l'aide d'un sonomètre.
Donner
un ordre de grandeur du niveau d'intensité acoustique mesuré dans le
cas d'une conversation entre deux personnes.
De 40 à 50 dBa.
Le moteur peut être assimilé à une source ponctuelle émettant de
manière isotrope. Soit r la distance entre la source supposée
ponctuelle et le point considéré où l'intensité I est mesurée.
Expliquer
pourquoi I est du type I = k/r2 ,où k est une
constante.
L’intensité acoustique est la
puissance
transportée par les ondes sonores perpendiculairement à une direction
donnée, par unité de surface.
Si le son est rayonné de manière isotrope, la puissance acoustique P de
la source se répartit dans l'espace, à travers des surfaces sphériques
S = 4 pr2 dont la
source est le centre.
Par suite I = P/S = P /(4pr2).
On obtient la courbe suivante avec un sonomètre mesurant le niveau
acoustique de l'onde émise par le moteur à différentes distances r.
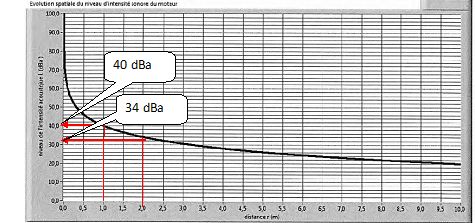
Relever
le niveau d'intensité acoustique L(r) pour r = 1 m et puis pour r = 2
m. En déduire la variation DL du niveau
d'intensité acoustique associé à ces deux positions. Aurions-nous pu
prévoir cette valeur ? Justifier.
L(r) = 10 log ( I / Iref).
I(r=1) = k ; L(r=1) = 10 log (k/Iref). I(r=2) = k / 4 ;
L(r=2) = 10 log (0,25k/Iref).
DL = 10 log
(0,25k/Iref) - 10 log (k/Iref) = 10 log 0,25 = -6
dBa.
Dans une chambre à coucher, le niveau d'intensité acoustique acceptable
est de 20 dBa. Si une chambre est située à 1 m du moteur, par quel facteur,
noté a, devrons nous diviser l'intensité acoustique ?
Ichambre = 10ref 102. Intensité
acoustique à 1 m du moteur : I =10ref 104.
Ichambre / I = 0,01. L'intensité acoustique liée au moteur
doit être divisée par 100.
La séparation entre le local du moteur et les chambres est supposée
être en bois. Le moteur sera considéré comme une source sonore
monochromatique de fréquence f = 100 Hz.
On va s'intéresser à la fonction de transfert T de cet isolant c'est à
dire au rapport suivant T = It / Ii où Ii
est l'intensité acoustique incidente c'est à dire arrivant sur la paroi
et It
est l'intensité acoustique transmise juste après la paroi de bois. Pour
la cloison étudiée, on obtient les résultats suivants : T = 1 / (1+w2 / w02).
w est une
pulsation quelconque et w0
est une pulsation de référence propre au bois.
On donne la représentation de la fonction 10 log T en fonction de w/w0.
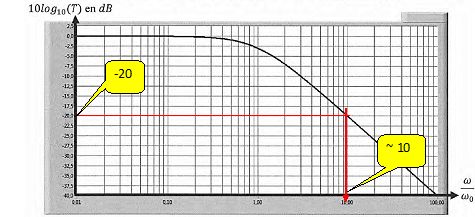
Exprimer en fonction
de w0, la pulsation wc de l'onde
acoustique pour laquelle l'atténuation de l'intensité acoustique est
égale à -3dBa.
T = It / Ii
; 10 log T = 10 log (It/ Ii ) = -3 ; It/ Ii = 10-0,3 = 0,50.
10 log T = 10 log [1 /
(1+w2
/ w02)] = -3 ; 1 / (1+w2
/ w02) = 10-0,3 = 0,50.
(1+w2
/ w02) = 2 ; w2
/ w02 = 1 ; w = w0.
Quel
est le pourcentage d'énergie acoustique transmise à partir de cette
pulsation de coupure ?
La coupure à - 3 dB correspond à une diminution de 50 % de l'énergie
acoustique.
On va chercher à dimensionner l'épaisseur de la cloison de bois pour
obtenir l'isolation souhaitée.
Comment
choisir la fréquence de coupure fc pour que
l'intensité acoustique de l'onde, de fréquence f = 100 Hz soit divisée
par un facteur 100.
It/ Ii = 0,01 ; 10 log T = 10 log 0,01 = -20 ; 10 log [1 / (1+w2
/ w02)] = -20 ; 1 / (1+w2
/ w02) = 10-2 = 0,01.
(1+w2
/ w02) = 100 ; w2
/ w02 = 99 ; w = 9,95 w0
; f = 9,95 f0 ; f0 =100/9,95 ~10 Hz.
A
quel domaine de fréquences appartient alors la fréquence de coupure
?
La fréquence de coupure se situe dans le domaine des infrasons.
Comparer
qualitativement l'atténuation, à travers l'isolant, d'un son grave et
d'un son aigu.
Fréquence des sons graves : 20 à 200 Hz : fréquence de coupure minimale
correspondante : ~2 Hz
Fréquence des sons aigus : 10 kHz à 20 kHz ; fréquence de coupure
correspondante ~2 kHz.
On montre que fc vérifie la relation suivante : fc
= r0c / (pra).
r0 =
1,2 kg m-3 : masse volumique de l'air ; c =340 m/s
célérité du son dans l'air ; r
= 950 kg m-3 masse volumique de l'isolant ; a : épaisseur de
l'isolant exprimée en mètre.
fc et "a" sont inversement proportionnels.
Les sons graves sont atténués par une épaisseur d'isolant plus grande que les sons aigus.
Quelle
est la valeur de a ?
a = r0 c / (p r fc) = 1,2*340 /
(3,14*950*10) =0,014 m.
Sur
quels facteurs pouvons nous agir pour améliorer l'isolation phonique
d'une pièce ?
Isoler phonétiquement la pièce des bruits extérieurs.
Corriger l'acoustique de la pièce en évitant les matériaux lisses (
utiliser des matériaux absorbants qui évitent la réflexion des sons sur
les parois).
Par contre il est difficile d'agir sur la taille et la géométrie de la
pièce.
|
|