Conversion d'énergie interne en énergie mécanique : Concours Capes 2013.

Au coeur d'une installation motrice à vapeur, l'eau subit une suite de transformations formant un cycle  ( le cycle de base est le cycle de Rankine ) au cours duquel elle se transforme en vapeur, à haute pression, elle se détend et met en rotation le groupe turbine-alternateur. Ce groupe convertit l'énergie mécanique en énergie électrique. Dans cette parties toutes les transformations étudiées seront réversibles. On donne les propriétés thermodynamiques de l'eau. T(°C) p(kPa) hl( kJ kg-1) hv( kJ kg-1) sv(kJ kg-1 K-1) sl(kJ kg-1 K-1) cpl(kJ kg-1 K-1) cpv(kJ kg-1 K-1) I 21 2,47 87,5 2540 8,65 ? 4,18 1,91 II 251 4030 1090 2800 6,07 2,81 4,88 4,03 III 374 22100 2080 2080 4,41 4,41 IV 477 4030 hl : enthalpie massique de l'eau liquide saturant, hv : enthalpie massique de l'eau vapeur saturante. < r <1. Le miroir M' sv : entropie massique de l'eau vapeur saturante, sl : entropie massique de l'eau liquide saturant. cpl et cpv sont respectivement les capacités massiques à pression constante  de l'eau sous forme liquide et de vapeur saturante. Enthalpie massique d'un corps pur fluide. Exprimer l'enthalpie massique h d'un fluide en fonction de son énergie interne massique u, sa pression P et son volume massique 1/µ. Préciser l'unité de h. h =  u + P V / m = u +P/µ.( V / m : volume massique ); h s'exprime en J kg-1. On considère le cas où le fluide est un corps pur diphasé, à l'équilibre à la température T, composé d'une phase liquide et d'une phase vapeur et on note x la fraction massique de vapeur. Exprimer l'enthalpie massique h du système en fonction de x, hv(T) et hl(T). h = x hv(t) + (1-x) hl(T). Premier principe de la thermodynamique appliqué aux fluides en écoulement permanent unidirectionnel. Un fluide s'écoule de façon permanente dans une conduite, depuis la section d'entrée où toutes les grandeurs sont indicées "e" jusqu'à la section de sortie où toutes les grandeurs sont indicées "s". On note respectivement Te, Pe et µe, la température, la pression et la masse volumique à l'entrée, et  en sortie les grandeurs homologues Ts, Ps et µs. Les énergies cinétiques massiques sont supposées négligeables, quant aux énergies potentielles massiques macroscopiques d'entrée et de sortie, elles ne varient pas. A l'entrée, l'enthalpie massique du fluide est notée he, à la sortie hs. 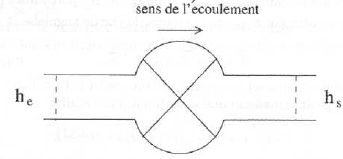Au centre du dispositif, le renflement marqué d'une croix représente le coeur du dispositif, là où le fluide qui passe peut recevoir le travail massique utile wu, qui représente le travail massique reçu autre que celui des forces de pression à l'entrée et à la sortie, et la chaleur massique qth. Ces deux grandeurs wu et qth sont les énergies reçues par le fluide au passage par le renflement, ramenés à l'unité de masse du fluide. Dans ces conditions le premier principe, ramené à l'unité de masse, pour la transformation depuis l'état initial à l'entrée, jusqu'à l'état final en sortie s'écrit : hs-he = wu + qth. Que représente hs-he si la transformation est adiabatique ? La transformation étant adiabatique qth=0 et hs-he = wu, travail massique utile reçu par le fluide. Que représente hs-he si le fluide s'écoule dans un échangeur thermique dans lequel il n'échange aucun travail utile ? wu = 0 et hs-he = qth, chaleur massique échangée. Entropie massique d'un corps pur fluide et lecture du diagramme entropique T(s). On donne le diagramme entropique de l'eau au cours d'une transformation isobare. La courbe de saturation qui limite le domaine où existe l'équilibre entre la vapeur et le liqude est représentée en tirets gras. Sont représentés en tirets fins les courbes le long desquelles la fraction massique x de la vapeur est constante pour x =0,1, x=0,2, x=0,3 etc. Placer les domaines de coexistence du liquide et de la vapeur, d'existence de la phase gazeuse et d'existence de la phase liquide. Le domaine vapeur est situé du côté des entropies élevées. 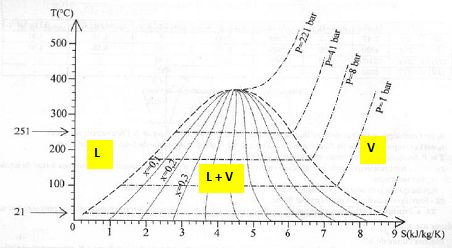Justifier l'existence d'un palier sur une isobare dans un diagramme entropique. Dans un mélange biphasé liquide vapeur, deux phases sont en équilibre, la variance est égale à 1.  Une isotherme est également une isobare. Si le fluide est biphasé à la température T, composé d'une phase liquide et d'une phase vapeur, de sorte que la fraction massique de vapeur soit notée x, exprimer l'entropie massique s du système en fonction de x, sv(T) et sl(T). s = x sv(T) + (1-x) sl(T). En considérant la vaporisation complète d'un kilogramme d'eau, dont l'état initial est liquide saturant, isotherme à la température T, établir le lien entre sl(T), sv(T), hl(T), hv(T) et T. Le changement d'état séeffectue à température et à pression constantes :  hv(T)- hl(T) = Qth = T ( sv(T) -sl(T) ). 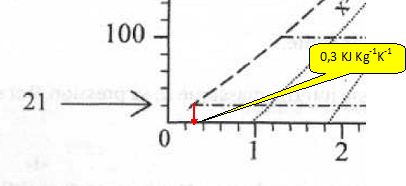Compléter la ligne I du tableau en calculant sl. Comparer à la valeur lue sur le graphique. sl(T) = sv(T) -[ hv(T)- hl(T)] / T = 8,65 -[2540-87,5] / (273+21) =0,31 kJ kg-1 K-1. Commenter les valeurs numériques fournies dans les lignes III et IV du tableau. 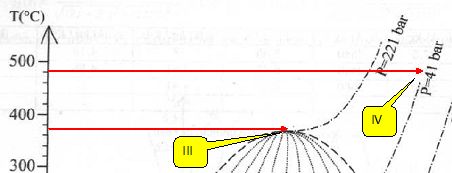III : le fluide est à l'état critique. Il n'y a plus de différence qualitative entre liquide et gaz. IV :  le fluide est à l'état gazeux. 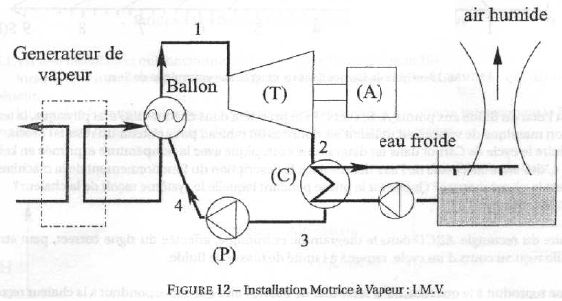Dans le générateur de vapeur (G V) l'eau est transformée en vapeur. Les tubes vaporisateurs traversent l'échangeur thermique dans lequel passe aussi le fluide caloporteur issu du coeur du réacteur. L'eau diphasique n'est pas totalement vaporisée dans les tubes, mais les phases vapeur et liquide sont séparées par gravité dans le ballon de sorte que le fluide en 1 soit bien de la vapeur saturante. La transformation de l'eau 4 --> 1 dans le générateur de vapeur est isobare. Dans la turbine T  la vapeur se détend de la haute pression à la basse pression, la transformation  1 --> 2 est adiabatique. L'eau se condense dans le condenseur C par échange de chaleur avec un fluide froid provenant d'un fleuve par exemple. Cette transformation 2 ---> 3 est isobare. La transformation 3 ---> 4 dans la pompe est adiabatique. La puissance nécessaire à la pompe est prélevée sur l'arbre de la turbine. Par ailleurs, la transformation d'énergie mécanique en énergie électrique est effectuée par un alternateur A et une alimentation  en eau froide provenant d'une rivière assure le refroidissement et la condensation de l'eau après passage par la turbine. La figure suivante représente le cycle de Carnot sur le diagramme entropique de l'eau. 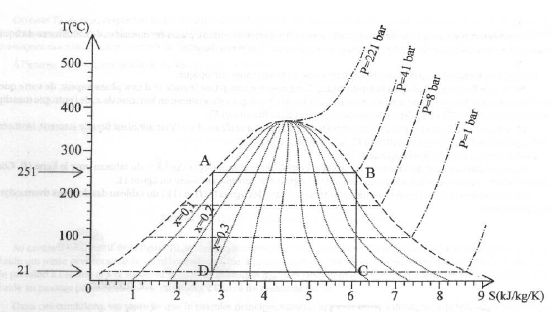Quel est l'état du fluide au points A, B, C et D ? A : liquide T = 251 °C, P =40,3 bar, fraction massique de la vapeur x = 0. B : vapeur, T = 251 °C, P = 40,3 bar, x = 1. C : L + V, T = 21 °C, P =2,47 kPa, x = 0,7.  D : L + V, T = 21°C, P =2,47 kPa, x = 0,3. Reproduire ce cycle de Carnot en plaçant les numéros 1, 2, 3 et 4.. 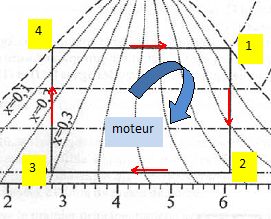Quelle est la phase motrice ? Quelle est la phase pendant laquelle le système reçoit de la chaleur ? Dans le générateur de vapeur le fluide reçoit de la chaleur. ( transformation 4 ---> 1 ). Dans la turbine la vapeur se détend et fait tourner le turbo-alternateur. ( phase motrice ). Rendement du cycle. Montrer que l'aire du triangle ABCD, avec le signe correct, peut être interprétée comme le travail utile reçu par le cycle, ramené à l'unité de masse du fluide. Aire du rectangle ABCD : (TA-TD) ( SB-SA). Au cours d'une transformation isobare, le travail est nul : W41 =W23=0. Q41 = T1( S1-S4). Q23 = T2( S3-S2) = T2( S4-S1). Au cours d'une transformation adiabatique, qth=0. Q12 = Q34 =0. La variation d'énergie interne du fluide est nulle sur un cycle. W + Q12 + Q34 +Q41 +Q23 =0. W = -(Q41 +Q23 ) =- T1( S1-S4) + T2( S1-S4) = (T2-T1)( S1-S4) = (TA-TD) ( SB-SA). Définir, puis calculer le rendement du cycle en fonction des températures extrèmes atteintes par le fluide Tmax et Tmin. Le rendement est le rapport entre le travail utile sur l'énergie dépensée. h = |W| / énergie reçue  avec  |W| = (Tmax-Tmin) ( SB-SA) et énergie reçue = Q41 = Tmax( SB-SA). h = (Tmax-Tmin ) /Tmax  = 1-Tmin /Tmax  = 1-(21+273)  / (273+251) =0,44. Le cycle de Carnot est un cycle idéal, pour lequel le rendement est maximal.

menu