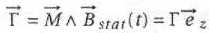|
|
Les
dispositifs qui permettent de transformer l'énergie mécanique en
énergie électrique sont le plus souvent des machines électriques
tournantes. Le phénomène d'induction électromagnétique permet de
comprendre le fonctionnement d'un alternateur.
Un alternateur, élément d'une éolienne, fournit en fonctionnement optimal une puissance électrique PN
= 6 kW. Le diamètre de ses pales est D = 5,6 m, sa vitesse de rotation
moyenne est de 150 tr/min. L'alternateur est à aimant permanent
Description de l'alternateur.
Le rotor est un solide de moment d'inertie J par rapport à l'axe Oz qui
peut tourner autour de cet axe. Il est repéré dans un référentiel lié
au stator par l'angle q(t). Le rotor a des propriétés magnétiques. Il peut être vu comme un aimant permanent, caractérisé par son moment magnétique 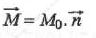 où M0 est le moment magnétique de l'aimant et n est un vecteur unitaire tournant contenu dans le plan xOy, repéré par l'angle q(t) qu'il fait avec Ox. Le rotor créé dans son environnement un champ magnétique que l'on notera où M0 est le moment magnétique de l'aimant et n est un vecteur unitaire tournant contenu dans le plan xOy, repéré par l'angle q(t) qu'il fait avec Ox. Le rotor créé dans son environnement un champ magnétique que l'on notera 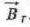
Le rotor est entraîné par un système mécanique non représenté, qui exerce un couple moteur de moment par rapport à l'axe Oz 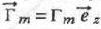 où Gm >0. où Gm >0.
On notera le couple de frottements 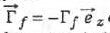 où Gf >0. où Gf >0.
Le stator de l'alternateur est constitué de deux associations de deux bobines ( B1, B'1) et (B2,B'2). Toutes les bobines sont identiques. Les bobines ( B1, B'1) ont leur axe commun, et leur sens de bobinage est identique. De même pour les bobines (B2,B'2).
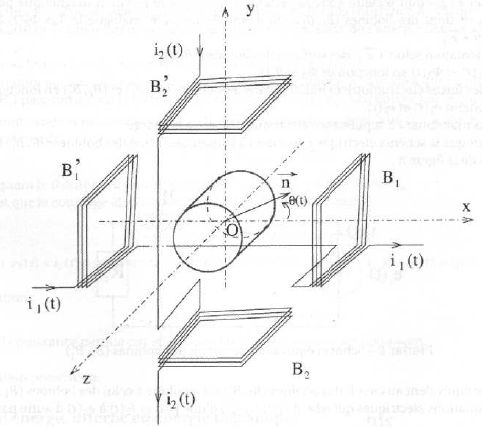
Chaque association de bobines forme un circuit qui est fermé sur une charge Rc. Chacune des bobines a une résistance r = 1 ohm et une autoinductance L = 0,2 mH.
Par la suite, on s'interesse au fonctionnement de l'alternateur en
régime permanent mécanique, c'est à dire, lorsque la vitesse de
rotation du rotor W est une constante positive. L'origine des temps est choisie de sorte que q(t) = Wt.
L'aimant du rotor est de type NdFeB.
Que signifie le sigle NdFeB ?
L'aimant est un alliage néodyme, fer, bore.
|
Nous commençons par étudier le phénomène d'induction qui se produit au stator de l'alternateur. Soit F(t) le flux d'un champ magnétique à travers un circuit filiforme quelconque fermé.
Rappeler la définition du flux du champ magnétique à travers le circuit.
Le vecteur surface est orienté d'après
le sens de parcours choisi sur le contour C.
Soit une surface s'appuyant sur le contour C. Le flux du
champ magnétique est conservatif et ne dépend
pas du choix de la surface; ce flux dépend du contour
C.
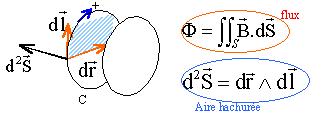
Enoncer la loi de Faraday qui relie la force électromotrice e(t) induite dans le circuit aux flux.
Un circuit fermé traversé par un flux magnétique F variable est le siège d'une force électromotrice
d'induction e=-dF/dt.
Le flux du champ magnétique Br à travers les bobines ( B1, B'1) peut s'écrire : 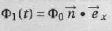 . .
On définit de manière analogue le flux à travers les bobines ( B2, B'2) :
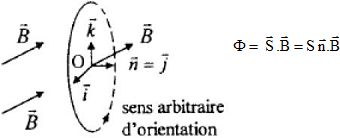
Justifier l'orientation suivant l'axe des x des surfaces des bobines ( B1, B'1).
Le vecteur surface est orienté d'après le sens du
courant ( sens arbitraire d'orientation ) dans les bobines : n un
vecteur unitaire normal à la spire dont le sens est fixé grâce à la
règle du tire-bouchon en fonction du sens arbitraire d'orientation de
la spire (un tire-bouchon tournant dans le sens d'orientation de la
spire progresse suivant n).
Exprimer F1(t) et F2(t) en fonction de F0 et q(t).
F1(t) = F0 cos q(t) ; F2(t) = F0 cos(½p- q(t) ) = F0 sin q(t).
En déduire les forces motrices idnduites dans les bobines.
e1(t) = -d F1(t) / dt = -F0 sin q(t) dq(t)/dt ; or q(t) = Wt : dq(t)/dt =W. e1(t) = -F0 W sin(Wt) = F0 W sin(Wt+p)= F0 W sin(Wt+½p).
e2(t) = -d F2(t) / dt = F0 cos q(t) dq(t)/dt ; e2(t) = F0 W cos(Wt).
Puissance électrique délivrée à la charge.
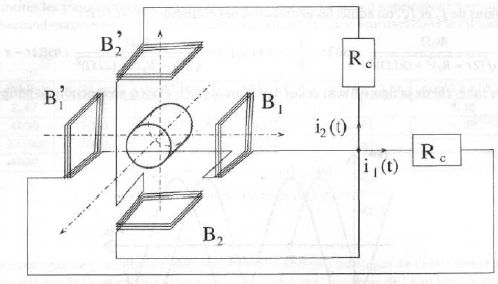
Justifier le fait que le schéma électrique équivalent à l'ensemble des bobines ( B1, B'1) fermées sur la charge Rc soit conforme au circuit ci-dessous :
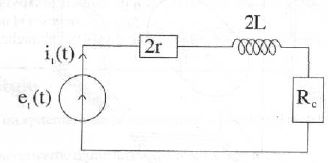
Les deux bobines identiques sont montées en série : les inductances et les résistances internes s'ajoutent.
Le schéma électrique équivalent au circuit des bobines ( B2, B'2) est similaire à celui des bobines ( B1, B'1).
Etablir les équations électriques qui relient i1(t) et e1(t) d'une part et i2(t) et e2(t) d'autre part.
e1(t) = (2 r + Rc) i1+ 2Ldi1(t) / dt.
e2(t) = (2 r + Rc) i2+ 2Ldi2(t) / dt.
Pour calculer les courants i1(t) et i2(t) on utilise la notation complexe. A la grandeur x(t) = Xm cos ( Wt + Y) on associe son amplitude complexe X = Xm e(jY).
Exprimer les amplitudes complexes associées aux intensites i1(t) et i2(t).
A e1(t) on associe : E1(t)=F0 W ejp/2 ; à i1(t) on associe I1 ; à di1(t) /dt on associe j W I1.
F0 W ejp/2 =(2 r + Rc) I1 + 2L j W I1 ; I1 = F0 W ejp/2 / ( (2 r + Rc) + 2L j W).
A e2(t) on associe : E2(t)=F0 W ; à i2(t) on associe I2 ejj ; à di2(t) /dt on associe j W I2 ejj.
F0 W =(2 r + Rc) I2 ejj+ 2L j W I2 ejj; I2 = F0 W e-jj / ( (2 r + Rc) + 2L j W).
A partir des expressions de I1 et I2, on admet les expressions de i1(t) et i2(t) :
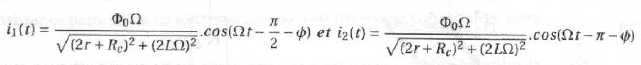
avec F = Arctan (2LW) / (2r+Rc)).
On donne les courbes représentant i1(t)et i2(t) en fonction du temps.
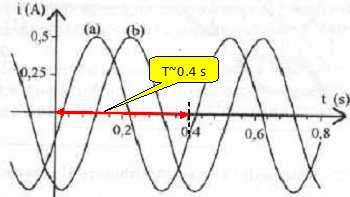
Faire correspondre aux courbes a et b les courants correspondants.
i1(t) est en avance de ½p sur i2(t) ; la courbe (a) est en avance de ½p sur (b) : la courbe (a) correspond à i1(t).
Déduire de ces courbes la vitesse de rotation du rotor.
La
période est T ~0,4 s ( lecture graphe ) ; La fréquence vaut 1/T = 1/0,4
= 2,5 Hz ou 2,5 *60 = 150tr/min, on retrouve la vitesse moyenne du
rotor correspondant à un fonctionnement optimum.
On note PC1 la puissance électrique moyenne délivrée à la résistance Rc.
Donner l'expression de Pc1 en fonction de F0, W et des éléments du circuit.
PC1 = Rc < i12(t) > =Rc (F0 W )2/ ( (2 r + Rc)2 + (2L W)2) <cos2(Wt-½p-F)>.
La valeur moyenne du terme en cos2 est égale à ½, d'où : PC1 = ½Rc(F0 W )2/ ( (2 r + Rc)2 + (2L W)2) .
On notera Pc2 la puissance délivrée par les bobines ( B2, B'2) à la résistance Rc à laquelle elles sont reliées.
Etudions
désormais le phénomène physique qui permet le transfert de l'énergie
depuis sa forme mcanique à sa forme électrique. Pour cela nous
considrons le système mécanique que constitue le rotor.
La liaison pivot du rotor sur l'axe Oz est parfaite ( son moment par rapport à l'axe ainsi que sa puissance sont nuls ).
Les bobines ( B1, B'1) parcourues par le courant i1(t) et les bobines ( B2, B'2) parcourues par le courant i2(t) crééent en O et son voisinage un champ magntique tournant Bstat(t) qui tourne à la vitesse W. Ce champ magnétique soumet le rotor à un couple de momemt : 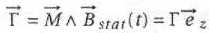
En appliquant le thorème du moment cinétique scalaire, relier G, Gf et Gm.
G - Gf + Gm= 0, en régime permanent.
On admet que le couplage électromagnétique se traduit ici par l'égalité : G W +<e1(t) i1(t) + e2(t) i2(t) >=0 où <e1(t) i1(t) + e2(t) i2(t) > représente la moyenne temporelle de e1(t) i1(t) + e2(t) i2(t).
En
déduire la relation : Gm W = Gf W + Pc1 +Pc2 +Pjoule.
Gm= -G + Gf ; GmW = -GW + Gf W = <e1(t) i1(t) + e2(t) i2(t) > + Gf W.
e1(t) = (2 r + Rc) i1(t)+ 2Ldi1(t) / dt ; e1(t) i1(t) = (2 r + Rc) i1(t) i1(t) + 2Ldi1(t) / dt i1(t).
En régime permanent, la puissance moyenne consommée par l'inductance est nulle.
<e1(t) i1(t)> = (2 r + Rc)< i1(t) i1(t)> + 2L<di1(t) / dt i1(t)> = 2 r < i21(t)> + Rc<i21(t)>= 2 r < i21(t)> +Pc1.
De même : <e2(t) i2(t)> = 2 r < i22(t)> +Pc2. En posant 2 r < i21(t)> +2 r < i22(t)> = Pjoule.
Par suite : Gm W = Gf W + Pc1 +Pc2 +Pjoule.
Cette relation traduit la conservation de la puissance totale :
Gm W : puissance mécanique fournie au rotor ; Gf W : puissance perdue par frottements ; Pjoule : puissance perdue par effet joule dans les bobines ; Pc1 +Pc2 : puissance électrique délivrée par les bobines.
|
|

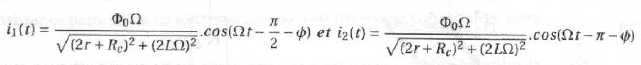

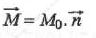 où M0 est le moment magnétique de l'aimant et n est un vecteur unitaire tournant contenu dans le plan xOy, repéré par l'angle
où M0 est le moment magnétique de l'aimant et n est un vecteur unitaire tournant contenu dans le plan xOy, repéré par l'angle 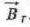
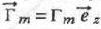 où
où 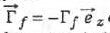


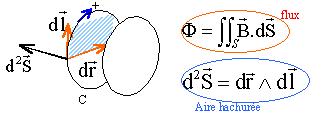
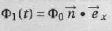 .
.