Modèle de l'atome, chimie quantique, spintronique : Agrégation 2013

Aurélie 31/01/13

Modèle de l'atome, chimie quantique, spintronique : Agrégation 2013.

Donner une vision synthétique de l'évolution du modèle de l'atome.
Démocrite, 420 avant JC, a l'intuition de l'existence des atomes ( "atomos" signifie en grec insécable).
Mais Aristote, philosophe grec, conteste cette existence, et son influence est si grande que l'idée de Démocrite ne réapparaît qu'au XIXème siècle.
En 1805, John Dalton propose le modèle de la boule de billard, sphère dure.
En 1881, J.J Thomson découvre l'électron, l'un des constituants de l'atome.
En 1904, Thomson pense que l'atome est électriquement neutre.
En 1910, Rutherford, en bombardant des feuilles d'or par des particules alpha montre que la masse de l'atome est pratiquement concentrée dans son noyau, minuscule par rapport au dimension de l'atome.
En 1922, Niels Bohr pense au modèle planétaire pour décrire un atome.
En 1925, l’avènement de la théorie quantique et l’équation de Schrödinger donnent une nouvelle approche du modèle de l’atome.

Dans un manuel scolaire de seconde, on propose l'exercice ci-dessous :
Donner la structure électronique de l'atome de sodium ²³₁₁Na et de l'atome de chlore ³⁵₁₇ Cl et en déduire la structure des ions sodium et chlorure.
Compétences attendues : utiliser le symbole ^A_ZX ; dénombrer les électrons de la couche externe ; connaître et appliquer la règle de l'octet.
Na : 11 électrons répartis ansi : premier niveau complet à 2 électrons, second niveau complet à 8 électrons ; le troisième niveau ne compte qu'un seul électron, celui-ci est facilement perdu et on obtetient l'ion sodium Na⁺ possédant une couche électronique externe saturée à 8 électrons.
Cl : 17 électrons répartis ansi : premier niveau complet à 2 électrons, second niveau complet à 8 électrons ; le troisième niveau compte sept électrons, l'atome gagne facilement un électron et on obtetient l'ion chlorure Cl^- possédant une couche électronique externe saturée à 8 électrons.

En 1885, Anders Jonas Angström, astronome et physicien suédois, pionnier dans l'étude des spectres, identifie quatre raies dans le spectre visible de l'hydrogène, de longueurs d'onde : 656,2 nm, 486,1 nm, 434,0 nm et 410,1 nm.

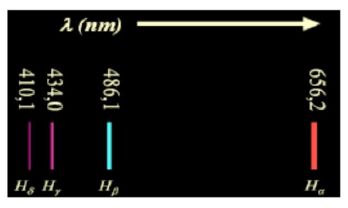
Johann Jakob Balmer, physicien et mathématicien suisse, établit alors empiriquement que ces quatre longueurs d'onde l peuvent s'exprimer par la formule : 1/l = G (n²-4) / n² avec n >2.
Cette formule, généralisée en 1888 sous la forme 1/l = R_H ( 1/p²-1/n²) par Walter Ritz et Johannes Rydberg, a été validée expérimentalement par la découverte de nouvelles raies d'émission de l'hydrogène dans le domaine de l'UV.
Dans cette relation p est un entier ( indice de la série) et n un entier ( indice de la raie) avec n > p.
A partir de la formule établie par Balmer, attribuer les valeurs de n ( n = 3, 4, 5, 6) aux 4 raies du spectre visible de l'hydrogène en explicitant la démarche.
A la plus petite longueur d'onde l correspond la plus grande valeur de 1 / l.
(n²-4) / n² = 1 -4 / n² est d'autant plus grand que n est plus élévé.
n = 6 correspond donc à 410,1 nm ; n= 5 à 434,0 nm ; n=4 à 486,1 nm et n = 3 à 656,2 nm.
Montrer que la constante de Rydberg est égale à et déterminer la valeur de cette constante.
G (n²-4) / n² = G ( 1-4 / n²) = 4 G ( 1 / 2² -1/n²) identifié à R_H ( 1/p²-1/n²) avec p = 2 pour les raies visibles.
R_H =1 / (l ( 1 / 2² -1/n²)) =1 /(410,1 10^-9(0,25-1/36)) =1,097 10⁷ m^-1.
En déduire que l'énergie E_n, des différents niveaux d'énergie de l'atome d'hydrogène est donnée par la relation E_n(eV) = -13,6 / n² avec n entier positif.
DE =E_p-E_n = h c / l avec E_p > E_n.
E_p-E_n = h c R_H ( 1/p²-1/n²) avec p < n.
Par suite E_n (J) = - h c R_H/ n² = -6,63 10^-34 * 3,00 10⁸ *1,097 10⁷ / n² = -2,182 10^-18/ n².
E_n(eV) = -2,182 10^-18/ (1,6 10^-19 n²) = -13,6 / n².
Définir l'énergie d'ionisation d'un atome et déterminer sa valeur pour l'atome d'hydrogène.
C'est l'énergie qu'il faut fournir à un atome pour arracher un électron( le moins lié ) à l'état gazeux.
Cette énergie vaut 13,6 eV pour l'atome d'hydrogène pris dans son état fondamental.
Comment expliquer à des élèves de première S, que cette étude spectroscopique a permis de faire évoluer le modèle de l’atome ?
L’expérience qui montre que seules quelques valeurs de l’énergie sont permises. C’est le spectre discret de l’atome
d’hydrogène.
Le physicien danois Niels Bohr propose en 1913 une première théorie permettant d’interpréter l’existence des raies d’absorption et d’émission. Pour cela, il utilise le modèle planétaire de l’atome adopté à l’époque et quantifie le moment cinétique de l’électron, ce qui lui permet de justifier la formule expérimentale de Balmer. Cependant, ce modèle ne permettant pas d’expliquer le spectre des atomes autres que l’hydrogène et la structure hyperfine des raies de l’hydrogène mise en évidence par Zeeman, la théorie de Bohr est mise en défaut. En 1925, l’avènement de la théorie quantique et l’équation de Schrödinger donnent une nouvelle approche du modèle de l’atome.

.

De la chimie quantique à la spintronique.
La résolution de l’équation de Schrödinger permet de déterminer la fonction d’onde Y_{n, l, m}(r, q, j) associée à l’électron de l’atome d’hydrogène, (r, q, j) étant les coordonnées sphériques. Cette fonction peut s’écrire sous la forme : Y_{n, l, m}= R_{n, l} (r)Y_{l, m}(Q, j), R_{n, l} (r)étant la partie radiale et Y_{l, m}(Q, j) la partie angulaire.
Indiquer à quoi correspondent les indices n, l et m.
Ce sont les trois nombres quantiques décrivant une orbitale atomique de l'électron.
n : nombre quantique principal ; l : nombre quantique secondaire ou azimutal ; m : nombre quantique tertiaire ou magnétique.
On donne les expressions mathématiques des parties radiales des fonctions d’onde 1s et 2s :
R_1,0 = A exp(-r/a₀) et R_2,0 = A' (2-r/a₀) exp (-r / (2a₀)).
Justifier les indices dans la notation R_1,0 et R_2,0.
R_1,0: n = 1 , la seule valeur possible pour l est n-1 = 0 ; R_2,0: n = 2 ,l = 0 correspond à l'orbitale notée "s".
On appelle densité de probabilité radiale P_n,0(r) la quantité 4 p r²[ R_{n, 0}(r)]². La figure ci-dessous donne les courbes représentant l’évolution de P_n,0(r) en fonction de r/a₀ pour n = 1, 2 et 3.

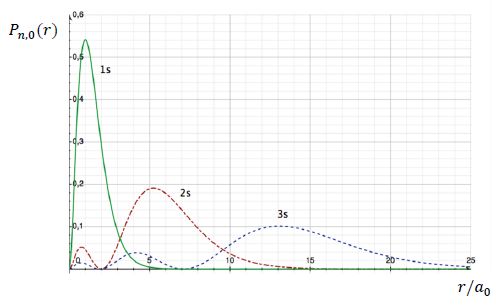
Comment utiliser la courbe P_1,0(r) pour expliquer à des élèves la différence existant entre le modèle classique (modèle de Bohr) et le modèle quantique de l’atome d’hydrogène.
Le modèle de Bohr est basé sur le modèle planétaire de Rutherford. L'électron parcourt différentes orbites circulaires quantifiées autour du noyau.
Dans le modèle quantique de l'atome, on considère que l'électron occupe de manière probabiliste certaines régions de l'espace autour du noyau.
On ne peut attribuer aux électrons des trajectoires bien définies mais seulement des probabilités de présence.
La probabilité est maximale au premier rayon de Bohr.
Quel schéma simplifié de l’atome d’hydrogène, pris dans son état fondamental, peut-on donner pour le modèle quantique ?

A quoi correspondent les maxima des courbes ?
Au maxima des courbes, la probabilité de trouver un électron est maximale.

Pour décrire le comportement des électrons des atomes, la fonction d’onde seule ne suffit pas, il faut lui adjoindre le spin. La genèse de ce concept au début du XXème siècle a été d’autant plus difficile que ce moment cinétique intrinsèque n’a pas d’équivalent en mécanique classique. Pour l’électron, le spin est égal à ½h .
Quelles sont les deux valeurs que peut prendre le nombre quantique de spin ?
Le nombre quantique de spin ne peu prendre que deux valeurs : ±½.
Représenter symboliquement un électron dans chacun des deux états de spin appelés « up » et « down ».
Une flèche vers le haut symbolise un électron de spin +1/2 (électron dit de « spin up »).
Une flèche vers le bas symbolise un électron de spin −1/2 (électron dit de « spin down »).

Alors que l’électronique actuelle repose sur la charge électrique de l’électron, la spintronique exploite la propriété quantique du spin de l’électron.
Un chercheur français a été colauréat du prix Nobel de physique en 2007 pour ses travaux sur la magnétorésistance géante (Giant Magneto Resistance GMR) en lien avec la spintronique.
Quel est le nom de ce chercheur ?
Albert Fert.
Considérons un électron 1s placé dans un champ magnétique extérieur B de direction verticale.
Formellement, l’état (ou la case quantique) 1s éclate en deux états (ou cases) d’énergies différentes. Nous parlerons de « décoration » d’une case quantique par le champ magnétique extérieur résultant en une case parallèle et une case anti-parallèle.
Représentation schématique du retournement du moment magnétique associé au spin plongé dans un champ magnétique. Les rectangles représentent les cases quantiques parallèle (à gauche) et anti-parallèle (à droite) décorées par un champ magnétique

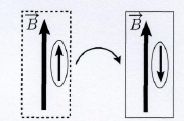
Si µ_B, magnéton de Bohr, désigne la valeur du moment magnétique associé au spin de l'électron, déterminer l'énergie de retournement E_flip ( en eV) pour passer de la situation parallèle à la situation anti-parallèle, la valeur du champ magnétique étant égale à 1 T.
E_flib = g µ_B B = 2*9,27 10^-24 *1 = 1,85 10^-23 J ou 1,85 10^-23 / (1,6 10^-19) = 1,16 10^-4 eV.
Finalement, un champ magnétique interagissant avec le spin de l'électron est susceptible de différentier les mouvements d'électrons "up" et "down" au sein d'un matériau.
Ecrire un texte comportant 15 lignes expliquant les termes " vanne de spin" et spintronique".
L'électronique actuelle repose sur une propriété essentielle de l'électron, sa charge électrique. La spintronique exploite une propriété supplémentaire de l'électron, la propriéé quantique de spin.
La magnétorésistance géante ( très sensible au champ magnétique, elle permet de diminuer la taille des zones de stockage des bits ) est très utilisée dans les têtes de lectures GMR des disques durs modernes.
Les données stockées sur un disque dur sont sous forme binaire, ( valeur 0 ou 1). L'aimantation du matériau magnétique ne peut pointer que dans deux directions opposées. Une aimantation pointant vers le "haut" codera, par exemple un 1, tandis qu'une aimantation pointant vers le bas codera un zéro.
La magnétorésistance géante ( GMR) peut être observée dans un matériau multicouches ( deux couches magnétiques séparées par une couche non-magnétique, d'épaisseur de l'ordre de quelques nanomètres ) en y faisant circuler un courant électrique.

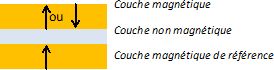
Si la couche non-magnétique est conductrice, on parle de "vannes de spin".
La résistance d'une telle structure dépend de l'orientation relative des aimantations des deux couches magnétiques. La résistance est faible si les deux aimantations pointent dans la même direction ( configuration parallèle ), grande si les deux aimantations pointent des directions opposées ( configurations anti-parallèles ).
Les électrons ayant la même orientation de spin que l’aimantation passent d’une couche à l’autre à travers l’épaisseur non magnétique sans être freinés, et il se crée un fort courant.

menu