Tramway et développement durable : BTS Travaux Publics 2012.

Etude partielle d'un chauffage collectif . Les tubes utilisés pour transporter l'eau chaude dans le réseau de chaleur sont calorifugés. Dans le réseau primaire, l'eau circule à 180°C sous 20 bars. On considère l'écoulement comme stationnaire : le débit massique qm est constant et vaut 565 kg h-1. La section des tubes diminue au fur et àmesure du trajet, lapression et la vitesse évoluent donc également. g = 9,81 m s-2 ; masse volumique de l'eau r = 1000 k m-3 ; diamètre tube 1 : D1 = 20 cm ; diamètre tube 1 : D2 = 16 cm ; presion dans le tube 1 : p1 = 5,0 bars ; 1 bar = 1 105 Pa. Détermination des vitesses. Calculer le débit volumique qv. qv = qm / r =565 / (3600 *1000 )= 1,57 10-4 m3 s-1. Donner l'expression littérale de la vitesse v1 dans le tube 1. La calculer. v1 =qv /( pR12)= 1,57 10-4 /(3,14*0,102) =5,0 10-3 m/s. Donner l'expression littérale de la vitesse v2 dans le tube 2. La calculer. v2 =qv /( pR22)= 1,57 10-4 /(3,14*0,082) =7,8 10-3 m/s. Quel est l'effet d'une diminution de section ? Un accroissement de la vitesse de l'eau. Détermination des pressions. Compléter le graphe en y indiquant les états liquide et gazeux de l'eau. 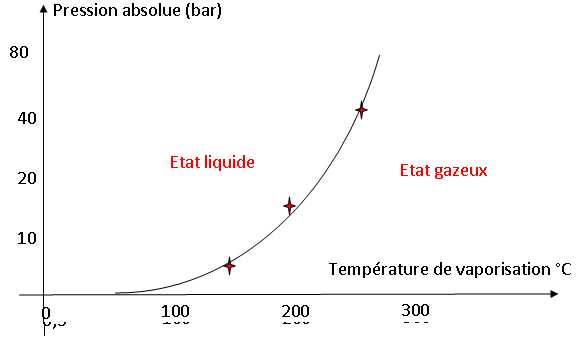Pourquoi l'eau du circuit primaire est-elle dite surchauffée ? L'eau est à l'état liquide à 180 °C sous 20 bars. Exprimer la dimension d'une vitesse v, de l'accélération g, d'une masse volumique r et d'une pression p. v = longueur / temps : [v] = L T-1 ; accélération = longueur / temps2 : [g] = L T-2. r = masse / volume = masse / longueur3 : [r] =M L-3. pression = force  / surface = masse * accélération / surface : [p]= M L T-2 L-2 = M L-1T-2. Vérifier l'homogénéité de l'équation de Bernoulli. ½r(v22-v12) + rg(z2-z1) +p2-p1 =0. [r(v22-v12)] =M L-3 (L T-1 )2 =  M L-1T-2, homogène à une pression. [rgz] =M L-3  L T-2 L = M L-1T-2, homogène à une pression.  Exprimer littéralement la pression p2. La calculer. ½r(v22-v12) + rg(z2-z1) +p2 -p1=0 ; p2 =p1 -½r(v22-v12) - rg(z2-z1). Si la canalisation est horizontale : z2-z1= 0. p2 =p1 -½r(v22-v12) = 5 105 -500((7,8 10-3)2-(5 10-3)2) =5 105 -0,018 ~ 5 bars. Pourquoi les valeurs de p1 et p2 sont-elles si proches ? Un liquide est difficilement compressible. De plus les diamètres des deux tubes sont trop proches pour provoquer une dépression  dans le tube 2. Etude de l'énergie thermique fournie. Plusieurs sous-stations d'échange sont réparties sur l'ensemble du réseau de chaleur afin de servir d'interface entre le réseau primaire et le réseau secondaire du client. Le débit dans les radiateurs étudiés est de 120 L/h. Initialement le chauffage de l'appartement était assuré par un chauffage électrique ppour une puissance totale P = 2750 W. Sur la nouvelle installation, l'eau entre dans le radiateur à 90 °C et en ressort à 70 °C. Eprimer puis calculer la masse d'eau circulant dans un radiateur en 12 h. m = qm Dt = qv r Dt= 120 10-3 / 3600*1000* 12*3600 = 120*12 = 1,44 103 kg. Exprimer puis calculer la quantité de chaleur fournie en 12 h par un radiateur. Capacité thermique massique de l'eau : c = 4180 J kg-1 K-1. Q = m c Dq = 1,44 103 *4180 *(90-70) =1,20 108 J. Exprimer puis calculer la puissance correspondante. P = Q / Dt = 1,20 108 /(12*3600) =2,79 103 ~2,8 103 W. On retrouve la même puissance de chauffage dans la nouvelle installation. Lutte contre le bruit. Le nouveau plan de circulation de la ville cherche à améliorer le confort acoustique de la population. Il associe la mise en place d'un tram avec la diminution du nombre de voies pour les voitures. Le niveau de bruit devra être atténué d'au moins 4 dB. le boulevard étudié comporte trois voies à sens unique. On se place dans le cas où 9 voitures passent en même temps le long du boulevard.  l'aménagement pour le passage du tram ne laissera plus qu'une voie pour le passage des voitures. On compare le bruit généré par le passage de 9 voitures circulant à 50 km/h au bruit généré par la passage du tram et de 3 voitures dont la vitesse vaut 50 km/h. Détermination du niveau de bruit lors du passage de 9 voitures. On enregistre au niveau de la façade de l'immeuble situé à 10 m du boulevard un niveau N d'intensité acoustique de 80 dB lors du passage d'une voiture roulant à 50 km/h. Exprimer littérallement le niveau d'intensité acoustique total N1 dû au passage de 9 voitures. Calculer N1. I = I0 10N/10 ; Itotal = 9 I = 9I0 10N/10 ; N1 = 10 log ( Itotal/ I0) =10 log (9 10N/10 ) =10 log (9 108) =89,54 ~90 dB. Le bruit engendré par le passage du tram roulant à 30 km/h est équivalent à celui d'une source sonore de puissance P = 40 mW émettant de façon isotrope dans toutes les directions. Exprimer littéralement l'intensité acoustique Itram en fonction de cette puissance P et de la distance d de l'immeuble. Calculer cette intensité. Itram = P / (4pd2) = 0,040 / (4*3,14*102) =3,18 10-5 W m-2. Calculer le niveau d'intensité acoustique Ntram. Ntram = 10 log(Itram / I0) =10 log( 3,18 10-5 / 10-12) =75 dB. Il passe simultanément au tram trois voitures émettant chacune un bruit de niveau d'intensité 80 dB. Calculer le niveau d'intensité acoustique total N2. Itotal = Itram + 3 I = 3,18 10-5 + 3I0 10N/10= 3,18 10-5 + 3 10-12 *108 =3,318 10-4 W m-2. N2 = 10 log(Itotal / I0 ) =10 log(3,318 10-4 / 10-12) =85,2 ~85 dB. Calculer l'affaiblissement acoustique et conclure. 89,54 -85,2 = 4,34 ~4,3 dB. L'objectif de réduction du niveau de bruit est donc atteint. Amélioration du bilan carbone. Le tramway n'émet pas de dioxyde de carbone car il fonctionne à l'énergie électrique. Par contre, la production d'énergie électrique peut dégager du dioxyde de carbone lorsque celle-ci est réalisée par des centrales à charbon ou à gaz. Dans le cas du tramway, toute l'énergie consommée sera produite grâce à une source d'énergie renouvelable. Masse volumique de l'essence : r = 750 kg m-3 ; consommation de la voiture : 7,0 L pour 100 km. Détermination de la quantité de dioxyde de carbone rejetée dans l'atmosphère par un véhicule à essence. On considère une essence constituée par un mélange d'hydrocarbures non cycliques de formule brute C8H18. A quelle famille appartiennent ces hydrocarbures ? Formule brute du type CnH2n+2 : alcanes. Ecrire la formule semi-développée  de l'hydrocarbure C8H18 linéaire et le nommer. CH3 -(CH2)6- CH3. Octane. Ecrire et équilibrer l'équation bilan associée à la combustion complète de cet hydrocarbure dans le dioxygène. C8H18 + 12,5 O2 ---> 8 CO2 + 9 H2O. Le véhicule étudié parcourt en moyenne 20 000 km par année. Exprimer et calculer la masse d'essence consommée en une année. Distance moyenne parcourue / 100 * consommation aux 100 km * masse volumique de l'essence. m =200 *7 10-3*750 = 1,05 103 kg. Exprimer et calculer la quantité de matière correspondante. M(C8H18) = 8*12+18 = 114 g/mol. n = m / M(C8H18) =1,05 106  / 114 =9,21 103 mol. Exprimer et calculer la masse de dioxyde de carbone rejetée en une année. nCO2 = 8 n ; M(CO2) = 44 g/mol ; mCO2 = nCO2 M(CO2)=9,21 103 *44 = 4,052 105 ~4,1 105 g ~4,1 102 kg. Expliquer en quelques mots ce qu'est l'effet de serre et conclure quant à l'intérêt de l'usage du tramway. Suite à la combustion du charbon, pétrole et gaz, la proportion de dioxyde de carbone augmente dans l'atmosphère. Or ce gaz piège la chaleur émise par la terre vers l'atmosphère. En conséquence la température moyenne de l'atmosphère croît de quelques degrés par siècle. Utiliser le tramway à la place des voitures en ville, diminue la quantité de dioxyde de carbone émis. .

menu