Dosage d'une solution aqueuse d'hydroxyde de sodium , installation triphasée, pompe à chaleur: BTS FEE 2013.

Dans une entreprise de traitement de l'eau, un bidon ancien est retrouvé. D'après l'étiquette, il contient une solution d'hydroxyde de sodium ( Na+ + HO-) de pH = 9,7. Le technicien désire vérifier la valeur du pH indiqué sur l'étiquette : pour cela il dose V =200,0 mL de cette solution par une solution d'acide chlorhydrique de concentration ca = 2,0 10-4 mol/L.Le volume d'acide versé à l'équivalence vaut VE = 15,8 mL. Cette solution est-elle ou acide ou basique ? Justifier . Une solution de pH supérieur à 7 à 25°C est basique. On suppose son pH égal à 7. Calculer  les concentrations en ion oxonium et hydroxyde. [H3O+]=10-9,7 =2,0 10-10 mol/L. [HO-]=10-14 / [H3O+]=10-14 / 10-9,7 =10-4,3 =5,0 10-5 mol/L. Ecrire l'équation de la réaction de dosage. H3O+aq + HO-aq ---> 2H2O(l). Déterminer la concentration de la solution d'hydroxyde de sodium. cb = caVE / V =2,0 10-4*15,8 / 200 =1,6 10-5 mol/L. En déduire la valeur du pH. L'indication de l'étiquette est-elle toujours correcte ? pH = 14 + log cb = 14 + log (1,6 10-5) =9,2. Ecart relatif : (9,7-9,2) / 9,2 ~0,05 ( 5%). L'indication est considérée comme correcte à 5 % près. Pour utiliser cette solution, qui reste trop concentrée, le technicien la dilue dans une grande quantité d'eau. Comment évolue le pH ? Vers quelle limite tend-il ? Par dilution d'une solution basique, le pH diminue et tend vers 7 à forte dilution. . Installation électrique. Le réseau triphasé 230 V / 400 V ; 50 Hz, alimente un atelier comprenant : - 9 lampes à incandescence identiques purement résistives : 100 W - 230 V ; - un moteur asynchrone triphasé M1 : Putile = Pu = 7,5 kW ; rendement h = 0,80 ; facteur de puissance cos f1 = 0,68. - un moteur asynchrone triphasé M2 : Pabsorbée = PM2 = 3,0 kW ; facteur de puissance cos f2 = 0,75. Tous ces appareils sont répartis sur les différentes phase de manière à ce que le système soit équilibré. Comment coupler une lampe sur le réseau ? Justifier. La tension aux bornes d'une lampe doit être égale à 230 V, cest à dire la tension simple. Une lampe sera donc branchée entre une phase et le neutre. Compléter le tableau suivant : 9 lampes moteur M1 moteur M2 installation Puissance active (kW) 0,9 7,5 / 0,8 =9,375 ~9,4 3,0 P=13,3 Puissance réactive ( kVAR) 0 9,4 tan f1 =10,13 ~10,1 3,0 tan f2=2,65 ~2,7 Q=12,8 Vérifier que la puissance apparente S de l'installation vaut 18,4 kVA. S = (P2+Q2)½ =(13,32 + 12,82)½ =18,4 kVA. Calculer la valeur efficace de l'intensité du courant en ligne. I= S / (3½U) =18,4 103 / (1,732*400) =26,56 ~26,7 A. Calculer le facteur de puissance de l'installation. cos f = P / S = 13,3 / 18,4 =0,723 ~0,72. Quel est l'intérêt d'avoir un facteur de puissance élévé ? Proposer une solution pour améliorer le facteur de puissance. Un facteur de puissance élévé diminue l'intensité en ligne, donc les pertes par effet Joule. En branchant des condensateurs en triangle, en amont de l'installation, on améliore le facteur de puissance. Etude du moteur M1. On donne la plaque signalétique de ce moteur : 230 / 400 V ; cos f1 = 0,68 ; Pu = 7,5 kW ; 1440 tr/min ; 50 Hz ; rendement : 80 %. Préciser la fréquence de synchronisme ns, le nombre de paires de pôles p et le gissement g. n = 1440 / 60 = 24 tr/s ou Hz ; ns est un peu supérieure à n : ns = 25 Hz ou 1500 tr/min. Nombre de paires de pôles : p = 50 / 25 = 2. Glissement g = (1500-1440/ / 1500 = 0,04. Exprimer puis calculer le moment du couple utile Tu en fonctionnement nominal. Pu = 2p n /60 Tu ; Tu = 60Pu/(2p n) =60*7500/(6,28*1440)=49,8 Nm.   Pompe à chaleur air- air. Cette machine fonctionne avec une source froide ( extérieur du local ) dont la température est qA = -8°C et une source chaude ( l'intérieur du local ) dont la température est qB = 20°C. Une quantité de matièred'air  n décrit le cycle suivant : A --> B : compression adiabatique réversible ; la température évolue de qA à qB. B --> C : compression isotherme. C --> D : détente adiabatique réversible. D --> : détente isotherme. Chaque état du système est caractérisé par sa pression p, son volume V et sa température T. l'air est considéré comme un gaz parfait. TA =265 K ; pA = 1,50 105 Pa ; VA = 0,800 m3 ; TB =293 K ; pC = 3,50 105 Pa ; Cv=20,8 J mol-1 K-1 ; g = 1,40. relation de Laplace : TVg-1 = constante. Montrer que n = 54,5 mol. n = pAVA / (RTA) =1,50 105 *0,800 / (8,314*265) =54,47 ~54,5 mol. Montrer que VB = 0,62 m3. La relation de Laplace s'écrit entre A et B ( adiabatique réversible )  :  VA g-1 TA = VB g-1 TB ; VB g-1 =VA g-1 TA /TB ; VB =VA(TA /TB)1/g-1. VB = 0,800 (265/293)2,5 =0,6223 ~0,622 m3. Calculer VC. On donne pB = 2,13 105 Pa. B---> C : compression isotherme : pB VB = pC VC. VC = pB VB / pC =2,13 105 0,622 / (3,50 105)=0,379 m3. 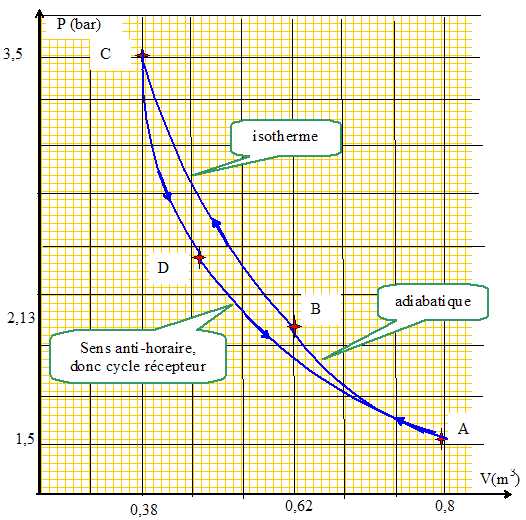Tracer l'allure du diagramme de Clapeyron ( p, V) du cycle, en indiquant les états A, B, C et D ainsi que le sens de parcours du cycle. La relation de Laplace s'écrit entre C et D ( adiabatique réversible )  :  pCVC g =pD VD g  = 3,50 105 *0,3791,4 =9,00 104. (1). Détente isotherme entre D et A : pA VA = pD VD = 1,50 105 *0,800 =1,2 105 (2). (1) / (2) donne : VD g-1  =9,00 104 / 1,2 105=0,75 ; VD   =0,752,5 =0,487 m3. Par suite : pD =1,2 105/0,487=2,46 105 Pa.

Donner la valeur de la chaleur reçue par l'air lors de l'évolution A ---> B. Evolution adiabatique QAB = 0. Justifier que le travail reçu par l'air lors de l'évolution A--> B est donnée par la relation : WAB = nCV(TB-TA). La variation de l'énergie interne de l'air entre A et B est WAB+QAB = nCV(TB-TA). QAB = 0, donc : WAB = nCV(TB-TA) = 54,5*20,8(293-265)=3,17 104 J. Montrer que le travail reçu par l'air lors de l'évolution B--> C s'exprime par la relation : WBC = -nRTBln(VC/VB). dWBC = -pdV avec p = nRTB / V ; dWBC = -nRTB dln V. Intégrer entre B et C : WBC = -nRTBln(VC/VB). WBC = -54,5 *8,314*293 ln(0,379 / 0,622) =6,58 104 J. En déduire QBC. Que signifie le signe de QBC ? La transformation B--> C étant isotherme et l'air étant considéré comme parfait, la variation de l'énergie interne de l'air est nulle : QBC+WBC =0 ; QBC = -6,58 104 J. L'air cède de la chaleur à l'intérieur du local. On note QDA la chaleur échangée par l'air avec le milieu extérieur lors de l'évolution D-->A. Exprimer l'efficacité e de cette machine en fonction de QBC et Wcycle, travail reçu par l'air au cours du cycle. e = -QBC / Wcycle. Exprimer l'efficacité e en fonction de QBC et QDA. La variation de l'énergie interne sur le cycle est nulle : Wcycle + QBC + QCD +QDA =0. QCD =0, évolution adiabatique. Wcycle = -QBC -QDA ; e = QBC / (QBC +QDA). On montre que e = TB / (TB-TA). Calculer e et conclure. e =293 / (293-265) =10,5. En dépensant une énergie de 1 J, la pompe à chaleur fournit 10,5 J au local à chauffer.

menu