Pompe à chaleur : chauffage d'une piscine, BTS chimiste 2013.

Dans un club de vacances, on construit une piscine rectangulaire couverte à proximité d’une retenue d’eau. Les caractéristiques de la piscine sont les suivantes : · Longueur a = 25,0 m ; largeur b = 15,0 m ; profondeur utile (hauteur d’eau) : h = 2,0 m · Température de l'eau de la piscine : Teau = 299 K ; température de l’air extérieur : Text = 283 K Constante du problème : · Chaleur latente massique de vaporisation de l'eau : Lvap = 2800 J.g-1. Mécanique des fluides. L'eau est puisée par quatre pompes dans le lac de retenue. La canalisation de sortie de chacune des pompes a un diamètre d = 50 mm. La vitesse du fluide dans cette canalisation est v = 3,0 m.s-1. Déterminer le débit volumique Qv d’une pompe. Section  de la conduite : S = pd2/4 =3,14 *(50 10-3)2/4=1,9635 10-3 m2. Débit Qv = S v =1,9635 10-3 *3,0 =5,89 10-3 ~5,9 10-3 m3 s-1. Déterminer Veau, le volume d'eau contenu dans la piscine. Veau = abh =25,0 *15,0*2,0=7,5 102 m3. En déduire Dt, la durée de remplissage de la piscine, les quatre pompes étant en service.  On exprimera Dt en heure. Dt = Veau / (4Qv) =750/(4*5,89 10-3 )=3,18 104 s =8,84 ~8,8 h Chauffage de la piscine. Après avoir procédé au remplissage de la piscine, une pompe à chaleur permet de maintenir constante la température de l'eau. La machine thermique fonctionne avec deux sources de chaleur (thermostats) : l'air extérieur de température Text et l'eau de la piscine de température Teau. Le fonctionnement de la pompe à chaleur est basé sur le cycle d'un fluide caloporteur. Le fluide caloporteur est initialement à l’état 1 sous forme d’un mélange liquide-vapeur. Le cycle est constitué des transformations suivantes : · Le fluide traverse l’évaporateur où l’air extérieur lui permet de subir une vaporisation complète de l’état 1 (p1, V1, T1) à l’état 2 (p2, V2, T2). · Le compresseur comprime ensuite isentropiquement cette vapeur de l’état 2  à l’état 3 (p3, V3, T3), augmentant sa température. · Au niveau du condenseur, la vapeur surchauffée voit sa température descendre jusqu’à Teau en suivant une transformation isobare de l’état 3 à l’état 4 (p4, V4, T4). · Le fluide, toujours comprimé, redevient ensuite liquide de l’état 4 à l’état 5 (p5, V5, T5). · La soupape de détente réduit la pression du fluide suivant le trajet de l’état 5 à l’état 1. Sur cette transformation, la température du fluide s'abaisse fortement, le rendant prêt pour un nouveau cycle. . On assimile la vapeur produite à un gaz parfait et on considère que toutes les transformations sont réversibles.  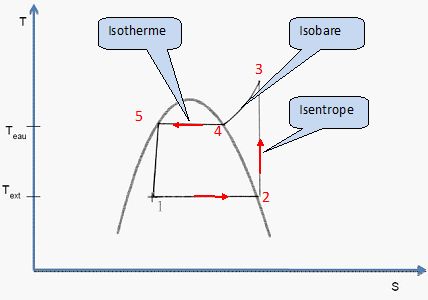Le schéma suivant donne l'allure de la courbe d'équilibre liquide-vapeur du fluide considéré dans le diagramme entropique (T, S). On y a tracé l’allure du cycle que suit le fluide et repéré le point 1 correspondant au début du cycle. Positionner les points numérotés de 2 à 5. Indiquer le sens de parcours du cycle. Justifier l’allure des courbes, représentant les transformations de l’état 1 à l’état 2, de l’état 2 à l’état 3 et de l’état 4 à l’état 5. La vaporisation du liquide s'effectue à température et pression constantes. La courbe 1 ---> 2 est donc un segment horizontal. La transformation 2 ---> 3 est isentrope : la courbe correspondante est un segment vertical. La transformation 3 ---> 4 est isobare : l'entropie est une fonction d'état. Sa variation ne dépend que de l'état final et de l'état initial. On imagine une transformation réversible allant de l'état 3 à l'état 4.  Variation élémentaire d'entropie : dS = Cp dT / T avec Cp indépendant de la température. dS= Cp d ln T. Puis intégrer de T3 à T4 : DS= Cp ln (T4 /T3 ). Transformation 4--5 : la vapeur se condense à température constante.( droite horizontale ). On considère le schéma suivant.  Sur le schéma, préciser quelle est la source chaude, quelle est la source froide et quel est le système. Indiquer par des flèches le(s) sens du (des) échange(s) thermique(s) et du (des) échange(s) de travail, ainsi que le signe de ces échanges. Préciser lors de quelle transformation chacun de ces échanges a lieu. 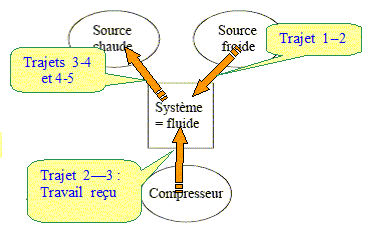La source chaude est la piscine ; la source froide est l'air extérieur. On adoptera les notations suivantes : chaleur échangée avec la source chaude : QC, chaleur échangée avec la source froide : QF, travail échangé : W. QC <0, le fluide cède de la chaleur à l'eau de la piscine. QF >0 : le fluide reçoit de la chaleur de l'air extérieur. W >0 : travail reçu par le fluide. On considère l’efficacité de l’installation de chauffage de la piscine. Donner la définition de l’efficacité e d’une pompe à chaleur. L'efficacité est égale à la valeur absolue de la chaleur gagnée par la source chaude divisée par le travail investi. En appliquant les deux premiers principes, montrer que l’efficacité maximale a pour expression : e = 1 / (1-Text / Teau).  Le premier principe s'écrit sur le cycle : DU=0 = W + Qfroide+Qchaude (1). Second principe : Qfroide/ Tfroide + Qchaude/ Tchaude <=0 (2). (1) donne : W= -Qfroide-Qchaude. e = -Qchaude / W = Qchaude / (Qfroide+Qchaude) e=1/ [Qfroide/ Qchaude+1 ] (2) donne : Qfroide/ Qchaude<= -Tfroide/ Tchaude . e <=1/ [1-Tfroide/ Tchaude ]. L'égalité correspond à la réversibilité.  Déterminer la valeur de l’efficacité maximale pour la pompe à chaleur de la piscine. e = 1 / (1-283/299) =18,7. En réalité l’efficacité e vaut : e réelle = 5. On considère que la principale perte d’énergie de l’eau de la piscine est due à l’évaporation. En effet le taux d’évaporation a par heure et par mètre carré de surface d’eau vaut : a = 150 g.h-1.m-2. En déduire Eperdue, l’énergie perdue par l’eau de la piscine pendant une heure. Masse d'eau évaporée en une heure : m =25,0*15,0*150 =5,625 104 g h-1. Eperdue = -m Lvap = -5,625 104 * 2800 = -1,575 108~ -1,58 108 J h-1. Quel est le travail reçu par la pompe à chaleur pour qu’elle puisse compenser la perte d’énergie Eperdue, due à l’évaporation pendant une heure ? eréelle = -Eperdue / W. W = -Eperdue / 5 = 1,575 108/5 =3,15 107 J.

menu