|
|
Objectif et oculaire sont modélisés par deux lentilles minces, respectivement L1 et L2, de centres optiques O1 et O2. Les distances focales de l'objectif et de l'oculaire sont respectivemet f'1 et f'2. L'intervalle optique est D = F'1F2.
L'angle sous lequel est observé l'objet AB à l'oeil nu est noté a.
L'objet
est observé à travers le microscope par un oeil normal sans
accomodation : on dit qu'il y a vision à l'infini. l'mage intermédiaire
est notée A1B1 et l'image définitive A'B' ; l'angle sous lequel est observée l'image finale est a'.
L'indice de réfraction du milieu considéré est noté n.
Grandissement de l'objectif |gobj| = 50, pour la vision à l'infini. Grossissement commercial de l'oculaire Goc = 20.
Ouverture numérique de l'objectif : n sin u = 0,70 ; D = 16 cm ; AB = 1 µm.
Pouvoir de résolution de l'oeil : 3 10-4 rad.
Grossissement commercial du microscope : Gc = a' / a = |gobj| Goc.
Pouvoir de résolution du microscope : e = 0,6 l / (n sin u).
Observation à l'oeil nu.
L'oeil de l'observateur est emmétrope, c'est à dire qu'il peut voir nettement un objet situé de l'infini à la distance inimale dm = 25 cm.
Calculer q angle sous lequel AB est vue, placé à la distance dm de l'oeil.
tan a = AB / dm = 10-6 / 0,25 = 4 10-6 ; a = 4 10-6 rad..
En déduire que la bactérie AB n'est pas visible à l'oeil nu.
q est inférieur au pouvoir séparateur de l'oeil : la bactérie n'est donc pas visible à l'oeil nu.
Vision à l'infini.
Le microscope est réglé pour que l'image finale soit rejetée à l'infii.
Quel est l'intérêt d'un tel réglage ?
L'oeil observe sans fatigue, sans accomoder.
Convient-il à toute vision sans correction ?
Cela convient seulement pour un oeil emmétrope.
Où se trouve l'image intermédiaire pour que cette condition soit vérifiée ?
L'image intermédiaire se trouve alors au foyer objet F2 de l'oculaire.
Grandissement du microscope.
Faire un schéma sans respect dechelle du microscope permettant de comprendre son fonctionnement.
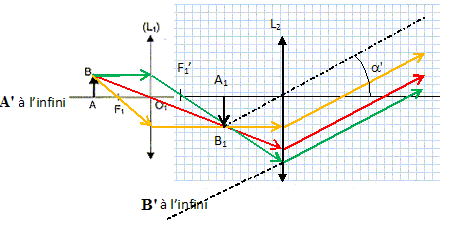
Montrer que |gobj|= D / f'1.
|gobj|= |A1B1 |/ AB = F'1A1 / O1F'1 ( voir schéma ).
Pour une observation à l'infini, les points F2 et A1 sont confondus et D = F'1 F2, d'où |gobj|= D / f'1.
Calculer f'1 et sa vergence C1.
f'1 = D / |gobj| = 0,16 / 50 =3,2 10-3 m = 3,2 mm. C1 = 1/f'1 = 1 /(3,2 10-3) = 3,1 102 d.
|
.
.
Observation de la bactérie AB.
Calculer le grossissement commercial Gc et en déduire a'. La bactérie est-elle maintenant visible ?
Gc = a' / a = |gobj| Goc = 50 *20 = 1000.
a' = 1000 a = 1000*4 10-6 = 4 10-3 rad, valeur supérieure au pouvoir séparateur de l'oeil : la bactérie est maintenant visible.
Pouvoir de résolution du microscope.
La
diffraction de la lumière à travers l'objectif limite l'utilisation du
microscope. On définit ainsi le pouvoir de résolution du microscope
noté e.
Calculer e pour l = 500 nmet en déduire si la bactérie est observable à travers cet instrument.
e = 0,6 l / (n sin u) = 0,6 *500 10-9 / 0,70 = 4,3 10-7 m = 0,43 µm.
La
taille de la bactérie étant supérieure au pouvoir de résolution du
microscope, celle-ci est donc observable à travers l'instrument.
Pourquoi l'observation de bactéries de taille beaucoup plus petite nécessite-t-elle d'immerger l'objectif dans un bain d'huile ?
Il faut augmenter le pouvoir de résolution du microscope, c'est à dire faire diminuer la valeur de e.
Pour cela il faut augmenter l'ouverture numérique n sin u, donc faire
croître n, indice de réfraction du milieu où baigne l'objectif.
|
.
|