|
|
L'industrie
automobile est amenée à concevoir de nouvelles technologies afin de
prendre en compte l'épuisement des ressources naturelles pétrolières.
Ces nouvelles technologies ont aussi pour objectif de réduire l'émssion
de dioxyde de carbone ainsi que la pollution.
Plusieurs constructeurs proposent à la location des véhicules équipés
d'une pile à combustible ( PAC). Il s'agit souvent de systèmes hybrides
associant une pile à combustible à dihydrogène et une source secondaire
d'énergie réversible ( batterie ou supercondensateur ). Ces différentes
sources d'énergies, associées à l'électronique de puissance, alimentent
un moteur électrique.
L'hydrogène,
vecteur énergétique.
Stockage
du dihydrogène dans un véhicule équipé d'une pile à combustible.
Le dihydrogène est assimilé à un gaz parfait. Une masse m = 6,80 kg de
dihydrogène gazeux est stockée, sous la pression atmosphèrique normale P0
=1,01 105 Pa = 1,01 bar et à la température de
20°C soit T0 ~293 K.
Calculer
la quantité de matière correspondante.
n0 = m / M(H2) = 6,8 103
/ 2 = 3,4 103 mol.
Donner
l'équation des gaz parfaits en précisant la signification des lettres
utilisées et l'unité de chaque grandeur.
PV = nRT.
P :pression ( Pa) ; V : volume (m3) ; n :
quantité de matière (mol) ; T : température ( K) ; R = 8,314 J mol-1
K-1.
Montrer
que le volume V0 de 6,80 kg de dihydrogène sous
la pression P0, à 20°C est supérieur à 80 m3.
V0
= n0RT0 / P0
= 3,4 103
*8,314*293 / (1,01 105) =82,0 m3.
Sous la pression P0, cette quantité de
dihydrogène ne peut pas être stockée dans un véhicule. Le stockage
s'effectue dans des conteneurs composites en matériau polymère étanche
au gaz et résistant aux fortes pressions.
Déterminer
graphiquement la pression P à l'intérieur d'un réservoir de 150 L.
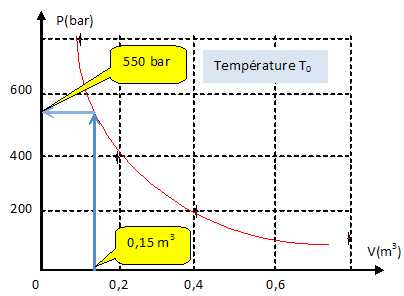
A
partir du tableau ci-dessous, indiquer si le dihydrogène peut être
considéré comme parfait dans le réservoir. Justifier.
| P(bar) |
T(K) |
V(m3) |
| 1,0 |
293 |
82 |
| 700 |
293 |
0,150 |
n = PV / (RT) = 700 105
*0,15 /(8,314*293) = 4,3 103 mol sous 700 bar.
Ecart relatif : (n-n0) / n0
= (4300-3400) / 3400 ~0,26 ( 26 %).
Cet écart est trop grand, le dihydrogène ne peut pas être considéré
comme parfait dans le réservoir.
|
Pile à combustible.
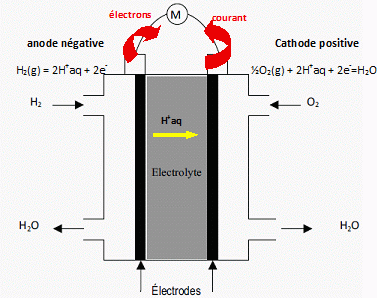
A l'anode, lecombustible utilisé est le dihydrogène du couple H+aq
/ H2(g) : H2(g) = 2H+aq
+ 2e-.
A la cathode, le comburant est le dioxygène du couple O2(g)
/ H2O(l) : O2(g) +4H+aq
+ 4e-= 2 H2O(l)
Indiquer
le sens du déplacement des électrons ainsi que le sens du courant
électrique. ( voir schéma ci-dessus )
Ecrire
l'équation de la réaction d'oxydorédution qui se produit dans la pile.
2 H2(g) = 4H+aq + 4e-.
O2(g) +4H+aq + 4e-=
2 H2O(l).
Ajouter : 2 H2(g) +O2(g)
+4H+aq + 4e- = 4H+aq
+ 4e- + 2 H2O(l).
Simplifier : 2 H2(g) +O2(g)
= 2 H2O(l).
On étudie la consommation du dihydrogène en fonction du temps. On donne
les résultats des mesures :
| V(H2)
(mL) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
| t(s) |
0 |
11 |
24 |
35 |
47 |
60 |
71 |
83 |

Donner
le coefficient directeur de la droite et en déduire la consommation
volumique moyenne en L s-1 .
Coeficient directeur a = 1,687 mL s-1 soit 1,687
10-3 L s-1.
Montrer
que la consommation molaire moyenne est n(H2) /
t = 7,00 10-5 mol s-1.
Vm = 24,1 L mol-1.
1,687 10-3 / 24,1 = 7,00 10-5
mol s-1.
Montrer
que la quantité de matière d'électrons échangés, notée n(e), et la
quantité de matière de dihydrogène consommée, notée n(H2)
vérifient : n(e) = 2n(H2).
H2(g) = 2H+aq + 2e-.
D'après les nombres stoechiométriques de cette demi-équation : n(e ) =
2 n(H2).
Montrer
que l'intensité débitée vaut I = 13,5 A. F = 96500 C mol-1.
Q = It = n(e) F ; I = n(e) F / t = 2*7,00 10-5*96500
/ 1 = 13,5 A.
Calculer
la puissance P fournie si la tension aux bornes de la cellule est 0,8 V.
P = UI = 0,8 *13,5 = 10,8 W.
La pile à combustible est un groupement de cellules élémentaires. La
puissance PT que doit fournir cette pile est
égale à 35 kW.
Calculer
le nombre de cellules élémentaires.
N = PT / P =35 103 / 10,8
~ 3,24 103.
Calculer
la durée de fonctionnement de ce véhicule.
Quantité de matière de dihydrogène consommé par seconde par la pile :
3,24 103* 7,00 10-5
=0,22685 mol s-1.
Quantité de dihydrogène stockée : 3,4 103
mol.
Durée de fonctionnement : 3,4 103
/ 0,22685 =1,498 104
s ~ 4,16 h ~4 h 9 min.
|
Etude
d'un supercondensateur.
Etude
de la charge à courant constant.

R = 50 mW.
Montrer
que uR est l'image de l'intensité I.
L'intensité et la tension aux bornes d'un conducteur ohmique sont
proportionnelles UR = RI.
L'image de la tension est celle de l'intensité au facteur I près.

Montrer
que I = 10 A.
I = UR / R = 0,5 / 0,050 = 10 A.
On peut utiliser divers résistances de 50 mW dont les puissances
maximales d'utilisation sont 3 W, 10 W, 25 W et 50 W.
Déterminer
le meilleur choix.
P = R I2 = 0,050 *102 = 5
W. On choisira la puissance immédiatemment supérieure soit 10 W.
Donner
la propriété essentielle d'une sonde de mesure de tension
différentielle. Justifier son utilisation pour visualiser UC.
On branche l'oscilloscope sans se soucier du problème de position de la
masse.
La relation qui lie la tension aux bornes du condensateur et
l'intensité est : I = CdUC/dt.
Calculer
la capacité C.
C = I / (dUC/dt) = 10 / (3 10-3)
=3,3 103 F.
|
Etude de la décharge.
Le condensateur étant complètement chargé sous la tension UC
= 2,7 V, on le décharge à travers un conducteur ohmique de résistance R
= 0,8 ohm. Un système d'acquisition permet d'entegistrer pendant 4 h
l'évolution de la tension aux bornes du condensateur en fonction du
temps
Déterminer
graphiquement la valeur de la constante de temps et en déduire C.
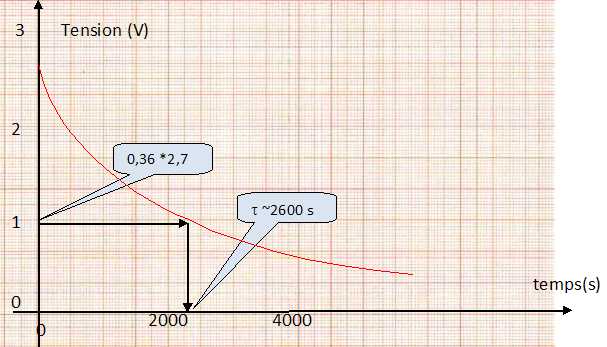
C = t / R = 2600 / 0,8
~3,3 103 F.
Stockage
de l'énergie.
Calculer
l'énergie ( en J et Wh) stockée par un condensateur de capacité C =
3300 F
soumis
à une tension U = 2,7 V.
½CU2
= 0,5 *3300 *2,72 =1,2 104
J ou 1,2 104 / 3600 = 3,34 ~3,3 Wh.
La masse du condensateur est m = 600 g.
Calculer
la valeur de l'énergie spécifique ( en Wh kg-1) et la
comparer à la valeur donnée par le constructeur 5,3 Wh kg-1.
3,34 / 0,6 = 5,57 ~5,6 Wh kg-1.
Ecart
relatif : (5,6-5,3 ) / 5,3 ~0,057 (5,7 %).
L'écart étant faible, les deux valeurs sont cohérentes. |
|





