|
|
Energie cinétique.
Dans le cadre de sa préparation physique, un sportif décide de faire une sortie en vélo.
Un chien traverse brusquement la route devant le cycliste et l’oblige à freiner pour ne pas le percuter.
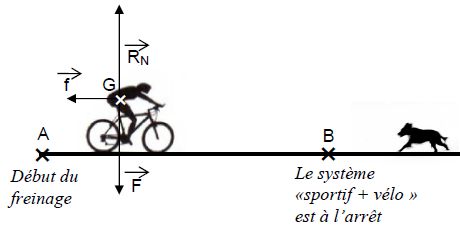
Le début du freinage se situe au point A où la vitesse du sportif est vA = 8,0 m.s-1. Au point B, le cycliste et son vélo sont à l’arrêt. On suppose la route horizontale et le mouvement du cycliste rectiligne.
Rappeler la relation permettant de calculer l’énergie cinétique d’un système en translation.
Ec = ½mv2 avec m en kg et v en m/s.
Montrer qu’au point A, la valeur de l’énergie cinétique est Ec(A) = 2500 SI en précisant
l’unité SI. La masse du cycliste et son vélo est m = 78 kg.
Ec(A) = 0,5*78*8,02 =2,496 103 ~2,5 103 J.
Justifier le fait que l’énergie cinétique au point B est nulle.
La vitesse en B étant nulle ( arrêt ), l'énergie cinétique en B est donc nulle.
Lors de son freinage, le cycliste et son vélo sont soumis à trois forces :
f représente les forces de frottement. RN est la réaction de la route.
Nommer la force F.
F représente le poids du cycliste et de son vélo.
Donner l’expression littérale du travail de la force de frottement W( f ) lors du déplacement
entre A et B en fonction de la valeur f de la force de frottement et de la distance de freinage d = AB.
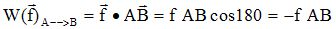
Énoncer le théorème de l’énergie cinétique.
La variation de l'énergie cinétique d'un système est égale à la somme
des travaux des forces extérieures appliquées au système durant cette
variation.
En appliquant le théorème de l’énergie cinétique entre A et B, on obtient l’expression : - 2500 = - f.d.
Calculer d sachant que f = 200 N.
d = 2500 / f = 2500 / 200 =12,5 m.
|
.
|
Ondes électromagnétiques.
Il
est tard, le cycliste rentre chez lui, aidé par les éclairages publics
qui pallient le manque de visibilité de ce début de soirée.
Certains éclairages fonctionnent avec des lampes à vapeur de sodium.
Cette vapeur est excitée par un faisceau d’électrons. Les atomes
absorbent l’énergie des électrons et la restituent ensuite sous forme
de radiations lumineuses de couleur orangée.
La fréquence ν est reliée à la célérité de la lumière dans le vide c par la relation : n = c/ l.
Que représente la grandeur λ dans cette relation ? Quelle est son unité dans le système international ?
La longueur d'onde l s'exprime en mètre.
Le domaine des longueurs d’onde des radiations visibles s’étend de 400 nm à 800 nm.
Calculer la valeur de la fréquence de la limite inférieure de ce domaine.
Donnée : c = 3,0 x 108 m.s-1.
n = 3,0 108 / (400 10-9) =7,5 1014 Hz.
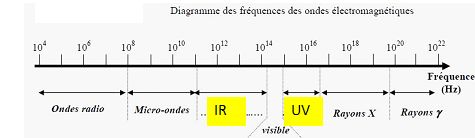
Compléter le diagramme des fréquences des ondes électromagnétiques en y faisant figurer les domaines :
- Infra-rouges (IR)
- Ultra-violets (UV).
|
|
La fréquence des radiations lumineuses émises par les lampes à vapeur de sodium est : ν = 5,1 x 1014 Hz.
Vérifier que l’énergie E d’un photon de ce rayonnement est environ égale à 3,4 x 10-19 J.
On donne E = h.ν où h est la constante de Planck : h = 6,62 x 10-34 J.s.
E = 6,62 10-34 *5,1 1014 =3,38 10-19 ~3,4 10-19 J.
L’énergie
d’un photon issu d’un rayonnement X est-elle plus ou moins grande que
celle calculée ci-dessus ? Justifier votre réponse.
Les photons X sont beaucoup plus énergétiques que les photons de la lumière visible.
Les fréquences des photons X sont bien plus grandes que les fréquences du visible.
|
|