|
|
Les joueurs et le ballon seront supposés ponctuels.
Sport de contact.
Il y a plaquage lorsqu'un joueur porteur du ballon, sur ses pieds dans
le champ de jeu, est simultanément tenu par un ou plusieurs
adversaires, qu'il est mis au sol et/ou que le ballon touche le sol. Ce
joueur est appelé joueur plaqué. D'après http://www.francerugby.fr.
Un joueur A de masse mA = 115 kg est animé d'une vitesse vA =5,0 m/s est plaqué par un joueur B de masse mB = 110 kg de vitesse négligeable.
Dans quel référentiel les vitesses sont-elles définies ?
Les vitesses sont définies dans le référentiel terrestre supposé galiléen.
On suppose que l'ensemble des deux joueurs est un système isolé.
Exprimer, en justifiant, la vitesse des deux joueurs liés après l'impact puis calculer sa valeur.
Ecrire la conservation du vecteur quantité de mouvement du système isolé constitué par les deux joueurs.
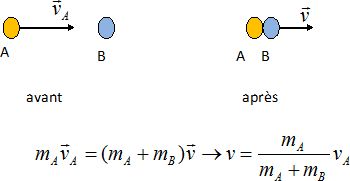
v = 115 / (115+110) *5,0 =2,555 ~2,6 m/s.
Sport d'évitement.
Une chandelle désigne un coup de pied permettant d'envoyer le ballon en
hauteur par dessus la ligne de défense adverse. L'objectif pour
l'auteur de cette action est d'être au point de chute pour récupérer le
ballon derrière le rideau défensif. D'après http://www.francerugby.fr.
On se place dans le référentiel terrestre supposé galiléen. Le champ de
pesanteur est considéré comme uniforme de valeur g = 9,81 N kg-1. On négligera toutes les actions dues à l'air.
Le joueur A est animé d'un mouvement rectiligne uniforme de vecteur vitesse v1. Afin d'éviter le plaquage, il réalise une chandelle au-dessus de son adversaire.
Le graphique ci-dessous représente la trajectoire du ballon dans le repère choisi.

A t = 0 le vecteur vitesse fait un angle a = 60° avec l'axe Ox et sa valeur est v0 = 10,0 m/s.
|
.
|
Etude du mouvement du ballon.
Etablir les coordonnées ax et ay du vecteur accélération du point M représentant le ballon.
Le ballon est en chute libre, il n'est soumis qu'à son poids. Ecrire la seconde loi de Newton :
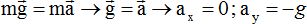
Montrer que les équations horaires du mouvement du point M sont : x =v0cos a t ; y = -½gt2 + v0 sin a t.
La vitesse est une primituve du vecteur accélération :
vx = constante = v0cos a ;
vy = -gt + constante ; vy(t=0) = v0 sin a ; vy = -gt +v0 sin a .
Le vecteur position est une primitive du vecteur vitesse. La position
initiale étant confondues avec l'origine du repère, les constantes
d'intégration seront nulles.
x =v0cos a t ; y = -½gt2 + v0 sin a t.
En
déduire l'équation de la trajectoire du point M.
t = x / (v0cos a) ; repport dans y :
y = - ½gx2 / (v0cos a)2 + x tan a.
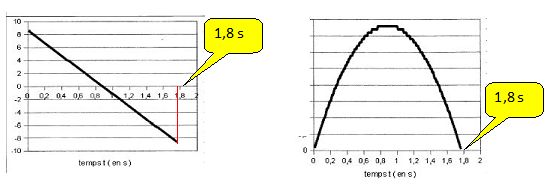
On donne les représentations graphiques de l'évolution au cours du temps des grendeurs x, y, vx et vy.
Ecrire sous chaque courbe l'expression de la grandeur qui lui correspond en justifiant.
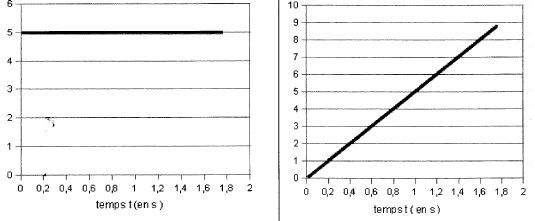
vx = constante = v0cos a = 5,0 m/s ; x =v0cos a t ( fonction linéaire croissante de coefficient directeur v0cos a ).
v0cos a = 10 cos 60 = 5,0 m/s.
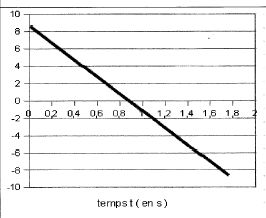
vy = -gt +v0 sin a . Fonction affine décroissante de coefficient directeur -9,81 m s-2 et d'ordonnée à l'origine v0 sin a = 10 sin 60 = 8,7 m/s.
|
|
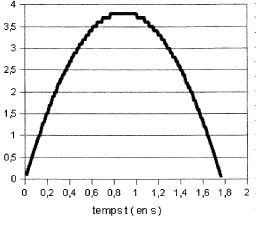
y = -½gt2 + v0 sin a t = -4,9 t2 +8,7 t. Arc de parabole.
Déterminer
par le calcul le temps dont dispose le joueur pour récupérer le ballon
avant que celui-ci ne touche le sol. Vérifier graphiquement.
-4,9 t2 +8,7 t = 0 ; t = 0 ( position initiale ) et t = 8,7 / 4,9 =1,8 s.
Déterminer de deux manières différentes la vitesse v1 pour que la chandelle soit réussie.
Distance parcourue par le joueur entre l'instant de la frappe et l'instant de la récupération : x =v0cos a t.
Vitesse du joueur animé d'un mouvement rectiligne uniforme : v1 =x/t = v0cos a = 10,0 cos 60 = 5,0 m/s.
Le mouvement du ballon suivant l'axe Ox et le déplacement du joueur
sont identique : ce sont des mouvements rectilignes uniformes à la
vitesse vx = 5,0 m/s.
|
|