|
|
Un
pendule simple est constitué d'un solide de masse m de petite taille
suspendu à un fil de masse négligeable et de longueur L très supérieure
à la taille du solide.
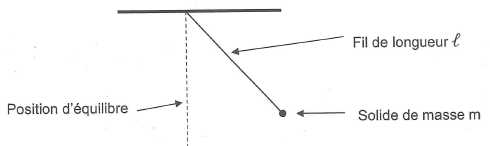
Ecarté de sa position d'équilibre, un pendule simple oscille
périodiquement après avoir été lâché. La période des oscillations
s'exprime par la relation T = 2 p
(L/g)½.
On donne : g = 9,81 m s-2 ; une coudée = 0,57 m.
Les
pendules de Galilée.
Discours concernant deux sciences nouvelles- Galilée ( 1638).
J'ai pris deux boules, l'une de plomb et l'autre de liège, celle-là au
moins 100 fois plus lourde que celle-ci, puis j'ai attaché chacune
d'elles à deux fils très fins, longs tous deux de 4 coudées ;
les écartant alors de la position perpendiculaire, je les lâchais en
même temps [...] ; une bonne centaine d'allées et venues, accomplies
par les boules elles mêmes, m'ont clairement montré qu'entre la période
du corps pesant et celle du corps léger, la coïncidence est telle que
sur 1000 vibrations comme sur cent, le premier n'acquiert sur le second
aucune avance, fût-ce la plus minime, mais que tous les deux ont un
rythme de mouvement rigoureusement identique.
On observe également l'action du milieu qui, en génant le mouvement,
ralentit bien davantage les vibrations du liège que celles du plomb,
sans toutefois modifier leur fréquence ; même si les arcs décrits par
le liège n'ont plus que cinq ou six degrés, contre cinquante ou
soixante pour le plomb, ils sont traversés en des temps égaux.
Citer
deux expressions employées dans le texte pour désigner une oscillation.
" d'allées et venue" et " vibrations ".
Comment
Galilée désigne-t-il la position d'équilibre du pendule ?
" la position perpendiculaire"
|
.
|
Répondre
aux trois questions suivantes en justifiant d'après le texte.
La mase m de la boule suspendue a-t-elle une influence sur la période
du pendule ?
"une
bonne centaine d'allées et venues, accomplies par les boules elles
mêmes, m'ont clairement montré qu'entre la période du corps pesant et
celle du corps léger, la coïncidence est telle que sur 1000 vibrations
comme sur cent, le premier n'acquiert sur le second aucune avance,
fût-ce la plus minime".
La période est indépendante de la masse de la boule suspendue.
Le pendule
en plomb est-il plus, moins ou autant sensible aux frottements que le
pendule en liège ?
"On
observe également l'action du milieu qui, en génant le mouvement,
ralentit bien davantage les vibrations du liège que celles du plomb".
" les arcs décrits par le
liège n'ont plus que cinq ou six degrés, contre cinquante ou soixante
pour le plomb".
Le pendule en plomb est peu amorti ;
le pendule en liège est très amorti.
La période
des oscillations dépend-elle des frottements ?
"sans
toutefois modifier leur fréquence ; même si les arcs décrits par le
liège n'ont plus que cinq ou six degrés, contre cinquante ou soixante
pour le plomb, ils sont traversés en des temps égaux".
La période des oscillations ne dépend pas des frottements.
Pourquoi
peut-on admettre que les pendules décrits dans le texte sont
asimilables à des pendules simples ?
Les boules sont de très petites dimensions et la longueur du fil est
bien supérieure au diamètre des boulles suspendues.
Calculer
la valeur de la période des pendules de Galilée.
L = 4*0,57 = 2,28 m ; T = 2*3,14 (2,28/9,81)½
=3,029 ~3,0 s.
Pendule dans un champ magnétique.
Pour
vérifier l'influence de la pesanteur sur la période d'un pendule
simple, il est difficile de se déplacer sur une autre planète. En
revanche, il est relativement simple de placer un pendule, constitué
d'un fil et d'une bille d'acier, à l'intérieur d'un dispositif
créant un champ magnétique uniforme dans une zone suffisamment large
pour englober la totalité de la trajectoire de la bille du pendule
pendant ses oscillations. Ce dispositif peut être constitué par des
bobines de Helmholtz.
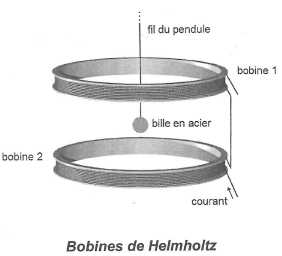
Lorsque
l'axe des bobines est vertical, le passage du courant électrique crée
un champ magnétique uniforme vertical dans la zone cylindrique situées
entre les deux bobines. Une bille en acier située dans cette zone est
soumise à une force magnétique verticale.
Expliquer pourquoi ce dispositif expérimental permet de simuler une variation de l'intensité de la pesanteur ?
La
bille en acier, placée dans un champ magnétique est soumise à une
force, verticale dans ce cas. Cette force vient s'ajouter ( ou se
retrancher ) au poids, suivant le sens du champ magnétique. Le
poids paraît plus grand ou plus petit. On simule ainsi une modification
de la pesanteur.
|
|
Comment doit être orientée la force magnétique exercée sur la bille pour simuler un acroisement de la pesanteur ? Justifier.
Le
poids apparent doit être supérieur au poids ; la force magnétique et le
poids doivent avoir le même sens, la verticale descendante.
Comment peut-on simuler un affaiblissement de l'intensité la pesanteur ?
En
modifiant le sens du courant électrique dans les bobines, on inverse le
sens du champ magnétique; on inverse ainsi le sens de la force
magnétique.
Si le dispositif a été correctement installé pour simuler un accroissement de la pesanteur, comment cela se traduit-il sur l'évolution de la période du pendule ? Justifier.
La période est inversement proportionnelle à la racine carrée de g ; si g augmente, alors la période diminue.
Le
système utilisé ne permet pas de simuler une forte variation de la
pesanteur mais il permet cependant de constater une variation de la
période, à condition de choisir un protocole optimisant la précision de
la mesure.
Proposer une méthode expérimentale pour obtenir une mesure la plus précise de la période.
Mesurer la durée d'une vingtaine d'oscillations puis diviser cette durée par 20 pour obtenir une valeur précise de la période.
Dans
le cas d'un pendule de longueur L = 0,50 m, on mesure une période de
1,5 s lorsque les bobines sont parcourues par un courant électrique.
Le dispositif simule-t-il un accroissement ou une diminution de la pesanteur ? Justifier.
En absence de courant dans les bobines T = 2*3,14 (0,50 / 9,81)½ =1,42 ~1,4 s.
En présence d'un courant on mesure une période plus grande ( 1,5 s ). La période étantt inversement proportionnelle à la racine carrée de g, le dispositif simule une diminution de la pesanteur.
Déterminer la valeur de l'intensité de la pesanteur apparente.
gapp = 4p2L/T2mesurée =4*3,142 *0,50 / 1,52 =8,77 ~8,8 m s-2. |
|