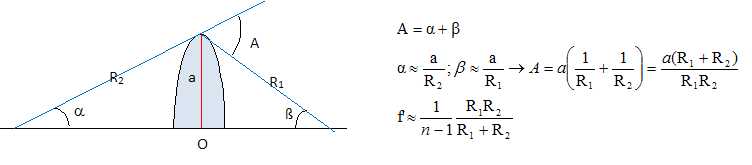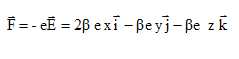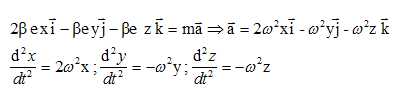|
|
Prisme.
Soit
un prisme d'angle A taillé dans un verre d'indice n. On considère
seulement les rayons situés dans un plan de section principale,
c'est-à-dire perpendiculaire à l'arête du prisme.
Un rayon lumineux arrivant sur le prisme avec l’angle d'incidence i
ressort du prisme avec l’angle d'émergence i'. Etablir
que l’angle de déviation D du rayon lumineux a pour expression : D = i
+ i' − A.
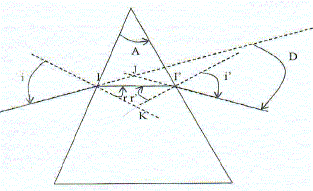
Les lois de Descartes relatives à
la réfraction en I et I' :
en I : nair sin i = n sin r soit sin i = n sin r
(1)
en I' : n sin r' =nair sin i' soit n sin r'= sin
i' (2)
Démonstration géométrique : r+r'=A
L'angle r a pour complément l'angle BII' ( en notant B le sommet du
prisme).
L'angle r' a pour complément l'angle BI'I ; d'où r+r'+ angle BII' +
angle BI'I= 180°.
de plus dans le triangle BII' : A + angle BII' + angle BI'I= 180°.
des angles ayant même supplément sont égaux, d'où : r+r'=A
Démonstration géométrique : D=i+i'-A
L'angle D a pour supplément l'angle IJI'
Dans le triangle IJI' :( i-r )+ (i'-r') + angle IJI' = 180 °
par suite D= ( i-r )+ (i'-r') = i+i'-(r+r') = i+i'-A.
Dans le
cas où i et A sont petits. montrer que D ~ (n-1) A.
i ~n r ; i' ~n r' ; i + i' ~ n(r+r') = n A ; puis D ~nA-A = (n-1) A.
Lentilles
minces.
Une
lentille est un milieu transparent qu'on suppose ici limité par deux
calottes sphériques ou par une calotte sphérique et un plan.
L'expérience montre qu'une lentille mince utilisée dans les conditions
de Gauss est stigmatique et aplanétique.
Qu'appelle-t-on
conditions de Gauss ?
Les
conditions de Gauss sont les conditions permettant d'obtenir une image
de qualité donnée par un instrument d'optique. Les rayons lumineux
doivent arriver sur les dioptres sous faible incidence.
Que
signifient les adjectifs stigmatique et aplanétique pour un instrument
d'optique ?
Stigmatisme : l'image d'un point est un point unique.
Aplanétisme : l'image d'un objet plan est plane.
On
se propose de retrouver directement les formules de Descartes
applicables ici à une lentille mince dans l'approximation de Gauss.
Pour cela, on considérera les rayons arrivant sur les bords de la
lentille mince assimilée à un prisme d'angle petit A. On se limitera au
cas d'une lentille biconvexe de rayon a. Toutes les grandeurs seront
considérées en valeur absolue sauf indication contraire. La lentille
constituée d'un verre d'indice n est supposée placée dans l'air.
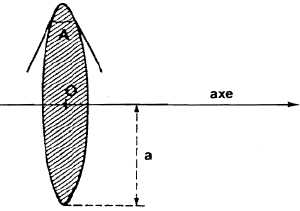
En
considérant les réfractions successives d'un rayon incident parallèle à
l'axe de la lentille, calculer la distance focale image f’ de la
lentille en fonction de n, A et a.
|
Calculer
de même la distance focale objet f. Exprimer f’ (ou f) en fonction
uniquement de n et des rayons R1 et R2 des
sphères limitant la lentille.
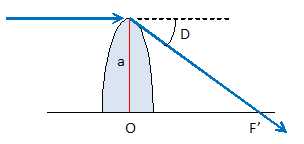
Dans l'approximation des petits angles : tan D = a / OF'~ D ; de plus D
~(n-1) A. Par suite : OF'~a /
((n-1)A). Par raison de symétrie f ' = f.
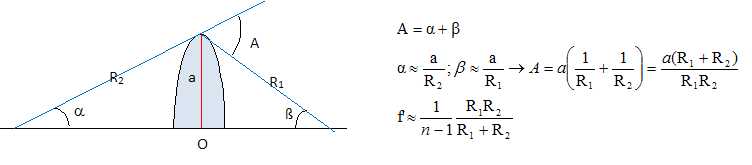
|
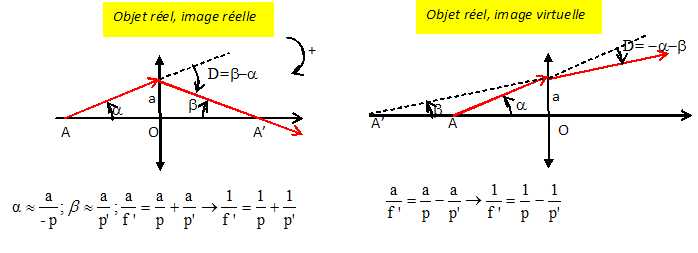
Soit
un point objet réel A situé sur l'axe de la lentille et donnant une
image réelle A'.
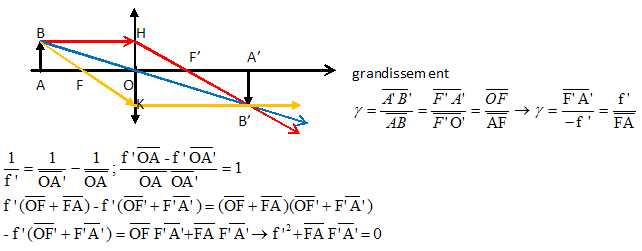
Retrouver
directement la relation de Descartes entre la position de l’objet et
celle de l’image. On posera p = OA, p' = OA' où O désigne
le centre optique de la lentille. Reprendre
la même question dans le cas où A est réel et son image virtuelle.
A
partir de la
relation de Descartes qu'on écrira ici en utilisant des grandeurs
algébriques, en orientant l'axe de la lentille dans le sens de
propagation de la lumière, trouver la relation dite de Newton.
|
Lentille
électrostatique.
Un
champ électrostatique E, non uniforme, règne dans une région R du
laboratoire. y2+z2<=
r2. ß est une constante, l
et r sont des longueurs données. On suppose r < l.
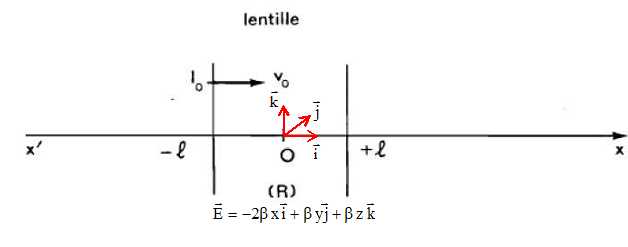
A l'instant choisi pour origine des dates (t = 0), un électron de
vitesse v0 pénètre en I0
dans R. A cet instant : x =x0 = -l ; y = y0<<
r ; z = z0<< r.
Quelle
est la forme de R ?
R est un cylindre. R porte dans la suite le nom de «
lentille électrostatique ».
Montrer
que, à l'extérieur de R, le mouvement d'un électron est rectiligne et
uniforme si on néglige son poids et l'action de tout autre champ
électrique ou magnétique.
Le principe d'inertie indique qu'un
système isolé est soit au repos ( si sa vitesse initiale est nulle),
soit animé d'un mouvement rectiligne uniforme.
Comment
choisir le signe de β si l'on veut que le champ E tende à maintenir
l'électron au voisinage de l'axe x'x ?
Dans la région R l'électron est soumis à la force : 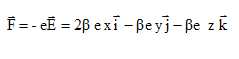
La
composante de cete force suivant l'axe des y doit être dirigée vers O :
si y >0 : -ße y doit être négatif soit ß >0. Si y
<0 : -ße
y doit être positif soit ß>0.
De même suivant l'axe des z.
Donner
l'expression du vecteur accélération d'un électron dans R. En déduire
les coordonnées du vecteur accélération en fonction de β, e, m et des
coordonnées x, y et z de l'électron. En déduire les équations
différentielles vérifiées séparément par x, y et z. On
posera w2
= ße / m.
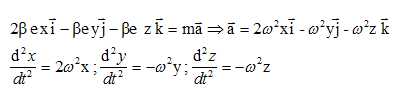
Vérifier
que la solution de l'équation différentielle en x est de la forme : x =
Aexp(kt) + Bexp(−kt) avec k > 0 et déterminer k en fonction de
ω.
Déterminer aussi A et B compte tenu des conditions initiales.
x'
= Ak exp(kt) -Bk exp(-kt) ; x" = Ak2 exp(kt) +Bk2
exp(-kt) ; repport dans l'équation différentielle vérifiée par x :
Ak2
exp(kt) +Bk2 exp(-kt) =2w2A
exp(kt) + 2w2
B ( exp(-kt).
Cette dernière égalité est vraie quel que soit le temps si k2
= 2w2 soit k
= 2½w.
x(0) =A+B =x0 ; x'(0) = k(A-B) = v0
; A = ½( x0 + v0/ k ) ; B = ½( x0 - v0/ k ).
|
|
Dans toute la
suite, on supposera satisfaite la condition v0
>> wl.
Montrer
que cette condition entraîne que la vitesse x' reste
pratiquement égale à v0.
A = ½( -l + v0/ (2½w) ) =½ /w ( -wl + v0/ 2½ )~½/w v0/ 21,5 ; B~ -½ /w v0/ 21,5.
x' = 2½ (A exp(kt) -B exp(-kt) ) ~ ½ v0 ( exp(kt) + exp(-kt).
Si
exp(kt) + exp(-kt) ~ 2, la vitesse est pratiquement égale à v0.
Dans
cette même approximation, résoudre
les équations en y et en z. Montrer que la trajectoire électronique
reste au voisinage de x’x (hypothèse paraxiale). Quelle est l'hypothèse
correspondante en optique ?
y" +w2y=0 ; solution générale : y = A cos (wt + B) où A et B sont des constantes déterminées par les conditions initiales.
y' = -A w sin (wt+B) ; y'(0) = 0 = A sin B ; A n'est pas nul, B = 0 ou p.
y(0) = y0 = A cos B ; si y0 >0, alors B = 0, d'où y = y0 cos (wt ). De même z = z0 cos (wt ).
y0 << r et z0
<< r : l'électron reste au voisinage de l'axe x'x, analogie
avec la condition de Gauss ( rayon lumineux proches de l'axe optique ).
Donner les coordonnées du
vecteur vitesse en I sur la face de sortie de la lentille. Donner les
coordonnées de la vitesse de l'électron en I.
L'électron sort du cylindre R à la date t = l /v0.
vx(½l) = v0 ; vy(½l) = -y0 w sin ( wl/v0) ~ - y0 w2l/v0 ~ -y0ßel/(mv0) ; vz(½l) = -z0ßel/(mv0).
Calculer les coordonnées
du point F’, intersection de la trajectoire de l'électron avec l'axe
x'x. La position de F' dépend-elle de I ? Justifier le nom de foyer
donné à F’.
On note t' la date de passage en F'. Au point F', yF' = -yI = -y0 cos (wl/v0) ~ -y0(1-(wl/v0)2) ~ -y0(1-(ße/m (l/v0)2).
yF' = -y0ßel/(mv0)t' ; par suite t' ~mv0/ (ßel) (1-(ße/m (l/v0)2).
xF' = v0t' =mv02/ (ßel) (1-(ße/m (l/v0)2).
xF' ne dépend pas de la position de I : tout rayon incident arrivant parallèlement à l'axe des x, émerge en pasant par F'.
Cette lentille électrostatique est-elle convergente ou
divergente ? Comment agir sur la distance focale de la lentille ?
xF' étant positive, cette lentille est convergente. On peut modifier xF' en modifiant v0 et / ou ß ( c'est à dire agir sur le champ électrique )..
A.N : calculer la distance focale OF' pour : l = 1,0
x 10−4 m ; wl/v0 =10-2.
xF' =v02 / (w2l)(1-(wl/v0)2) =l(v02 / (w2l2)(1-(wl/v0)2)=1,0
x 10−4 / 10-4 (1-10-4) ~ 1 m.
|