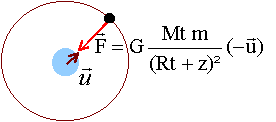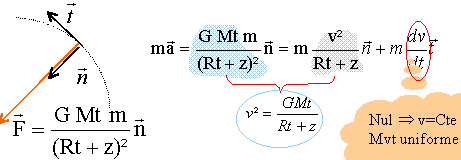|
|
À propos de la localisation.
Sortant tout juste d’une ville française, un automobiliste voit un
panneau indiquant Lyon à 240 km et Nancy à
340 km. Déterminer
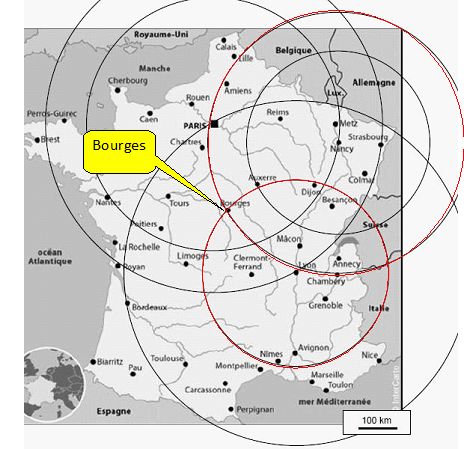
graphiquement, à l’aide de la carte fourniela ville où il se trouve.
Justifier.
100 km correspond à 1,2 cm sur la carte.
Tracer un cercle centré sur Lyon de rayon 2,4*1,2 = 2,9 cm.
Tracer un cercle centré sur Nancy de rayon 3,4*1,2 = 4,1 cm.
Il se trouve à Bourges, intersection des deux cercles.
Étude du mouvement d’un satellite
Le mouvement du satellite est étudié dans le référentiel géocentrique
supposé galiléen. Ce référentiel est associé au centre de la Terre
ainsi qu’à trois étoiles lointaines, considérées comme fixes.
En supposant que son orbite est circulaire, montrer que le
mouvement d’un satellite GPS de masse m est uniforme.
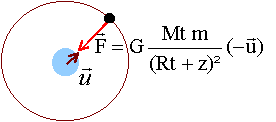
Le
satellite n'est soumis qu'à la force de gravitation centripète.
La
force de gravitation, perpendiculaire à la vitesse à chaque instant, ne
travaille pas et en conséquence ne modifie pas l'énergie cinétique du
satellite.
La valeur de la vitesse reste donc constante : mouvement uniforme.
Montrer
que l’expression de la vitesse du satellite est v = (GMt /(Rt+h))½ et déterminer sa
valeur numérique.
Mt = 5,98 1024 kg ; Rt =6,38 106
m ; altitude h =z = 2,00 107 m ; G = 6,67 10-11
SI.
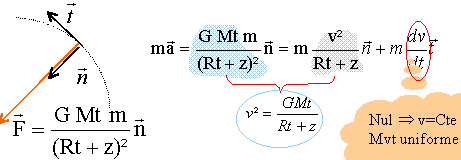
v = [( 6,67 10-11 *5,98 1024 ) / (6,38 106 +2,00 107 )]½
=3888,4 ~3,89 103 m/s.
Établir l’expression
de la période de révolution d’un satellite GPS. Calculer sa valeur et
vérifier qu’elle
est
compatible avec l’information du texte d’introduction. " deux
révolutions par jour autour de la terre".
Un satellite décrit une circonférence de rayon Rt+z
à la vitesse v durant une période T.
2p(Rt+z) = v T.
T
= 2p(Rt+z)
/ v = 2p(Rt+z)1,5
/(GMt)½.
T = 6,28 (6,38 106 +2,00 107 )1,5
/ ( 6,67 10-11 *5,98 1024)½ =4,26 104
s ou 11,8 h.
La période étant proche de 12 h, le satellite décrit deux révolutions
par jour.
|
.
|
Précision des mesures.
Justifier
par le calcul la phrase suivante : « Pour bénéficier d’une
précision de 10 m dans la direction de propagation du signal
électromagnétique envoyé par un satellite GPS, le récepteur GPS doit
mesurer la durée de trajet de ce signal avec une précision d’environ 30
ns. »
On note Dt la précision sur
la durée : Dt = 10 / (3,00 108)
=3,3 10-8 s = 33 ns.
Quelle
est la durée de parcours du signal électromagnétique ? En déduire la
précision relative sur la mesure de cette durée.
t = h/c = 2,00 107 / 3 108 = 6,67 10-2
s.
Précision relative : 3,3 10-8
/(6,67 10-2) ~5,0 10-7.
Si on ne tenait pas
compte des effets relativistes, quel serait le
décalage temporel entre les horloges terrestres et celles du satellite
GPS au bout d’une journée ? En déduire la durée nécessaire pour que les
horloges terrestres et celle du satellite GPS soient significativement
désynchronisées, c'est-à-dire pour qu’elles soient décalées de
30 ns.
La non prise en compte des effets relativistes entraine une avance des
horloges des satellites sur les horloges terrestres d’environ 38 μs par
jour.
Décalage temporel au bout d'une seconde : 38 10-6/(24*3600)=4,4
10-10 = 0,44 ns.
Les horloges sont désinchronisées au bout de : 30/0,44=68 s.
Étude du signal
GPS.
Sachant que le message GPS contenant les paramètres de calcul a une
taille d’environ 4,5 ko, calculer la durée
nécessaire à l’envoi de l’intégralité de ce message par le satellite
lors de la mise en marche du GPS.
Les informations sont envoyées par le satellite sous la forme d’un
signal binaire avec un débit très faible : 50 bit.s-1.
4,5 ko = 4500 octet ; un octet correspond à 8 bits.
Durée : 4500*8 / 50 = 7,2 102 s = 12 minutes.
Commenter
cette durée surprenante en s’appuyant sur le document «
Fonctionnement général du GPS ».
Cette durée ne correspond pas à la réalité.
Dans la pratique, le GPS garde en mémoire les paramètres du calcul de
position reçus avant son dernier arrêt et reprend par défaut ces
paramètres, lors de sa mise en marche.
|
En réalité, le
récepteur GPS reçoit en permanence des informations de plusieurs
satellites, sur une même fréquence. Pour distinguer les satellites les
uns des autres, on a attribué à chacun un code, appelé code C/A qui se
présente sous la forme de séquences binaires répétées de 1 et de 0. Le
message GPS est superposé à ce code et, lors de la réception du
message, le récepteur pourra, grâce au code, identifier le
satellite source et traduire le signal pour en connaitre le message.
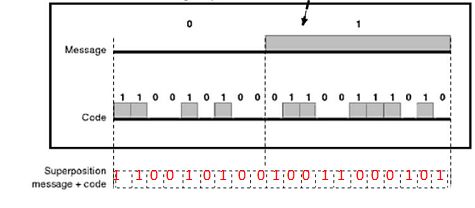
La superposition du code C/A et du message consiste simplement à
inverser les 0 et les 1 du code lorsque le bit du message vaut 1 et à
ne pas les modifier lorsque le bit du message vaut 0.
d’après science.gouv.fr
On donne un exemple de message GPS et de code C/A.
Compléter
cette annexe par 0 ou 1 en effectuant la superposition « message + code
» comme cela est indiqué dans le document « Fonctionnement
général du GPS » .
|
|